 και τη δυαδική πράξη
και τη δυαδική πράξη  η οποία ορίζεται ως εξής
η οποία ορίζεται ως εξής
Να δειχθεί ότι:
- η
 είναι αβελιανή ομάδα.
είναι αβελιανή ομάδα. -
 όπου
όπου  είναι η πολλαπλασιαστική ομάδα των θετικών πραγματικών αριθμών.
είναι η πολλαπλασιαστική ομάδα των θετικών πραγματικών αριθμών. - για όλους τους θετικούς ακεραίους
 και όλα τα
και όλα τα  ισχύει:
ισχύει:

- για όλους τους ακεραίους
 ισχύει
ισχύει



 ισχύει
ισχύει  , γεγονός που αποδεικνύει ότι η
, γεγονός που αποδεικνύει ότι η  είναι πράξη επί του
είναι πράξη επί του 
 και
και  αντιστρέψιμο με
αντιστρέψιμο με  .
.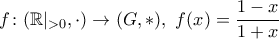 είναι ο κατάλληλος ισομορφισμός.
είναι ο κατάλληλος ισομορφισμός.
 και κάθε
και κάθε  ισχύει ότι
ισχύει ότι 
 βγαίνει το ζητούμενο.
βγαίνει το ζητούμενο.