Κάτι καινούριο στα Μαθηματικά...

DreamingMaths · #1

Φίλες και φίλοι των Μαθηματικών, Χριστός Ανέστη!

Έστω τα συστήματα μη γραμμικών εξισώσεων

$\left ( A1 \right )$
$x^{3}y+2x^{2}y^{3}-1=0$
$3xy^{3}+x^{3}y^{2}-2=0$

$\left ( A2 \right )$
$3x^{4}y+2x^{3}y^{4}-2=0$
$x^{4}y^{3}+2xy^{4}-3=0$

$\left ( A3 \right )$
$x^{5}-y^{5}-5x^{4}y+5xy^{4}+10x^{3}y^{2}-5x^{3}-10x^{2}y^{3}+10x^{2}y-x^{2}-5xy^{2}+5y^{2}-5xy+6x-5y=0$
$x^{6}+y^{6}-xy-2=0$

Γνωρίζω ότι δεν υπάρχει μαθηματική μέθοδος για να εξαγάγουμε εξίσωση ως προς μία μεταβλητή γενικά σε συστήματα μη γραμμικών εξισώσεων. Στη διάρκεια της πολυετούς μελέτης μου στις πολυωνυμικές εξισώσεις τρίτου, τετάρτου και πέμπτου βαθμού αντιμετώπισα παρόμοια συστήματα και κατόρθωσα με την αγάπη του Θεού που με ευλογεί ποικιλοτρόπως και τις φτωχές μου γνώσεις, αν και απόφοιτος Γενικού Λυκείου να συνθέσω μία μέθοδο για κάθε ανάλογο σύστημα η οποία κατορθώνει να εξαγάγει τελική εξίσωση ως προς μία μεταβλητή.

Δεν έχω κατορθώσει ακόμη να ολοκληρώσω τη μελέτη μου και να τη δημοσιεύσω στην Ε.Μ.Ε., για αυτό και δεν μπορώ να μιλήσω αναλυτικά για αυτές, μπορώ όμως να σας πω κάποια στοιχεία πληροφοριακά εάν ενδιαφέρεστε. Δεν χρησιμοποιώ κάποιο τέχνασμα αλλά μαθηματικές μεθόδους οι οποίες μπορούν να εφαρμοστούν σε ανάλογα συστήματα. Η μέθοδος διαφοροποιείται ανάλογα το βαθμό της μεταβλητής στην προς επίλυση εξίσωση, συνεπώς έχω τρεις διαφορετικές μεθόδους και εικάζω ότι μπορούμε να έχουμε ανάλογες μεθόδους και για εξισώσεις έκτου ή και μεγαλύτερου βαθμού. Το εικάζω γιατί δεν το έχω συνθέσει, μέσα μου όμως έχω μία απόλυτη σιγουριά.

Στο σύστημα $\left ( A1 \right )$ η μέθοδος κατορθώνει να απαλείψει τα κυβικά ριζικά που προκύπτουν κατά την αντικατάσταση και να συνθέσει τη ζητούμενη εξίσωση. Δείτε την εδώ.

ΕΜΦΑΝΙΣΗ ΚΕΙΜΕΝΟΥ

Στο δεύτερο σύστημα $\left ( A2 \right )$ καλούμαστε να λύσουμε μία εξίσωση τετάρτου βαθμού και να αντικαταστήσουμε στη δεύτερη. Η μέθοδος επίλυσης του Ferrari δεν προσφέρεται εδώ για να επιτευχθεί το ζητούμενο καθότι σε μία τυχαία εξίσωση που δεν έχει ρητή ρίζα, οι προκύπτουσες ρίζες του τύπου είναι πολυπλοκότατες. Το έχω αναφέρει ξανά σε παλαιά μου ανάρτηση, έχω κατορθώσει να συνθέσω έναν τύπο επίλυσης για τη γενική εξίσωση τετάρτου βαθμού μέσω μίας διακρίνουσας ο οποίος θεωρώ ταπεινά ότι είναι απλούστερος του Ferrari. Η μελέτη μου σε αυτή την εξίσωση μου έχει αποκαλύψει μία σχέση ανάμεσα στους παράγοντες των ριζών της τον οποίο χρησιμοποιώ για να απαλείψω τα ριζικά στο σύστημα. Η σχέση αυτή είναι απαραίτητη και ο τύπος του Ferrari δεν την αποκαλύπτει. Δείτε την εξαγόμενη εξίσωση εδώ.

ΕΜΦΑΝΙΣΗ ΚΕΙΜΕΝΟΥ

Για να κατορθώσουμε τον αυτό στόχο στο τρίτο σύστημα $\left ( A3 \right )$ και σε ανάλογα συστήματα θα πρέπει η εξίσωση πέμπτου βαθμού να είναι επιλύσιμη ως προς μία τουλάχιστον μεταβλητή. Η τρίτη μέθοδος είναι και η πιο όμορφη από τις τρεις και μένα προσωπικά με συναρπάζει! Ο μαθηματικός μου τύπος χρησιμοποιεί τα προκύπτοντα ριζικά πέμπτης τάξης για να συνθέσει τη ζητούμενη τελική εξίσωση και φέρνει αποτέλεσμα. Δείτε και αυτή την εξίσωση εδώ.

ΕΜΦΑΝΙΣΗ ΚΕΙΜΕΝΟΥ

Αν σας ενδιαφέρει ποια ρίζα της πεμπτοβάθμιας εξίσωσης πήρα για να εξαγάγω το ζητούμενο, δείτε την εδώ.

ΕΜΦΑΝΙΣΗ ΚΕΙΜΕΝΟΥ

Έστω οι εξισώσεις
$\left ( B1 \right )$
$y^{2}-y+2-(y-1){\sqrt[5]{y^{2}+3y-1}}+(2y^{2}-5){\sqrt[5]{(y^{2}+3y-1)^{2}}}-$
$(3y-2){\sqrt[5]{(y^{2}+3y-1)^{3}}}+(4y+1){\sqrt[5]{(y^{2}+3y-1)^{4}}}=0$

$\left ( B2 \right )$
$x^{2}-2x-1+(x-1)\sqrt[5]{2x+\sqrt{4x^{2}+1}}+(x-1)\sqrt[5]{2x-\sqrt{4x^{2}+1}}+$
$(x-\sqrt{4x^{2}+1})\sqrt[5]{(2x+\sqrt{4x^{2}+1})^{2}}+(x+\sqrt{4x^{2}+1})\sqrt[5]{(2x-\sqrt{4x^{2}+1})^{2}}=0$

Οι εξισώσεις αυτές έχουν μια πολύπλοκη μορφή (αν και ο όρος πολύπλοκη δεν είναι ο καταλληλότερος να τις χαρακτηρίσει). Δεν γνωρίζω αν αυτές μπορούν να επιλυθούν μέσω μαθηματικών μεθόδων. Αν αυτό συμβαίνει, παρακαλώ όπως με πληροφορήσετε. Πάντως το Wolfram Mathematica αδυνατεί να μου βγάλει τις ρίζες. Και σε αυτές τις περιπτώσεις χρησιμοποιώ κάποια δική μου μέθοδο για να εξαγάγω την πολυωνυμική εξίσωση που προκύπτει από τη κάθε μία απ' αυτές οπότε είναι δυνατή κατόπιν η εύρεση των ριζών τους. Δείτε τις εξισώσεις εδώ.
Για την $\left ( B1 \right )$ .

ΕΜΦΑΝΙΣΗ ΚΕΙΜΕΝΟΥ

Για την $\left ( B2 \right )$ .

ΕΜΦΑΝΙΣΗ ΚΕΙΜΕΝΟΥ

Τα σχόλια είναι δικά σας.

#2

DreamingMaths έγραψε: ↑
Σάβ Μάιος 07, 2022 4:20 pm
Δεν έχω κατορθώσει ακόμη να ολοκληρώσω τη μελέτη μου και να τη δημοσιεύσω στην Ε.Μ.Ε.,
...

Το εικάζω γιατί δεν το έχω συνθέσει, μέσα μου όμως έχω μία απόλυτη σιγουριά.

'Εχω δύο σχόλια.

α) Στο πρώτο σύστημα λες ότι βρήκες μέθοδο να αποφεύγεις κυβικές ρίζες. Μα αυτό είναι απλό και μάλιστα, αν το κάνεις σωστά, ούτε καν μπαίνουν στο προσκήνιο οι κυβικές ρίζες. Π.χ. το σύστημα γράφεται

x^2y(x+2y^2)=1

Με διαίρεση κατά μέλη έχουμε $\displaystyle{\dfrac {x(x+2y^2}{x(3y+x^2)}= \dfrac {1}{2} }$ που είναι δευτεροβάθμια ως προς

. Συγκεκριμένα

(2-y)x^2+4xy^2 -3y^2=0

.

Δίνει λοιπόν $x=A\pm \sqrt B$ όπου A,B

πολυώνυμα του

. Mε αντικατάσταση σε μία από τις αρχικές, απομόνωση του $\sqrt B$ και ύψωση στο τετράγωνο δίνει πολυωνυμική εξίσωση ως προς

. Πουθενά δεν εμφανίστηκαν κυβικές ρίζες. Από εκεί και πέρα δεν έκανα τις πράξεις γιατί δεν αξίζει τον κόπο αλλά έκανα έλεγχο με λογισμικό το οποίο μου έδωσε την ενδεκάτου βαθμού εξίσωση που γράφεις, δηλαδή την $36y^{11}-5y^{8}+12y^{7}-12y^{6}-24y^{5}+y^{3}-6y^{2}+12y-8=0$ .

Με λίγα λόγια δεν βλέπω τίποτα το εξαιρετικό που να δικαιολογεί τον τίτλο και τα υπόλοιπο περιεχόμενο του ποστ.

β) Ομολογώ ότι δεν πιστεύω ότι η όποια μέθοδος έχεις (που μόνος σου λες ότι δεν την έχεις ολοκληρώσει) θα οδηγήσει σε λύση τέτοιων συστημάτων. Το μόνο που θα πετύχει είναι να καταλήξει σε μία πολυωνυμική εξίσωση (πράγμα απλό) αλλά από εκεί και πέρα δεν προχωράει. Γιατί; Για τον απλούστατο λόγο γιατί η γενική 5-βάθμια και πάνω δεν λύνεται με ριζικά. Οπότε αν πέσουμε σε μία επιλύσιμη, φρακάραμε.

Ας δούμε ένα τέτοιο παράδειγμα:

Να λυθεί το σύστημα

x^3y-x=1

Η δεύτερη φυσικά δίνει y=x^2

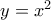που με αντικατάσταση στην πρώτη δίνει $\boxed {x^5-x-1=0}$ .

Συνέχισε!

Δεν θα τα καταφέρεις γιατί η εν λόγω εξίσωση είναι (το στάνταρ) παράδειγμα μη επιλύσιμης με ριζικά πεμπτοβάθμιας εξίσωσης.

Όπως και να είναι, θα χαρώ να δω την λύση σου.

Απλά κάνω την ευχή να μην επαναληφθεί η ιστορία εδώ (βλέπε ιδίως τα ποστ #10 και #12).

Κάτι καινούριο στα Μαθηματικά...

Κάτι καινούριο στα Μαθηματικά...

Re: Κάτι καινούριο στα Μαθηματικά...

Μέλη σε σύνδεση