2) Έστω τα ιδεώδη
 και
και  ενός δακτυλίου.
ενός δακτυλίου.Δείξτε
 . Ισχύει πάντα η ισότητα;
. Ισχύει πάντα η ισότητα;Συντονιστής: Demetres
 και
και  ενός δακτυλίου.
ενός δακτυλίου. . Ισχύει πάντα η ισότητα;
. Ισχύει πάντα η ισότητα; ώστε κάθε γνησίως φθίνουσα ακολουθία ιδεωδών της είναι πεπερασμένη.
ώστε κάθε γνησίως φθίνουσα ακολουθία ιδεωδών της είναι πεπερασμένη. είναι σώμα.
είναι σώμα. (ως προς ισομορφισμό), όπου
(ως προς ισομορφισμό), όπου  πρώτος.
πρώτος. το οποίο δεν είναι αντιστρέψιμο. Προφανώς,
το οποίο δεν είναι αντιστρέψιμο. Προφανώς,
 είναι το τελευταίο ιδεώδες στην αλυσίδα. Τώρα, το
είναι το τελευταίο ιδεώδες στην αλυσίδα. Τώρα, το  θα πρέπει να είναι ίσο με ένα από τα
θα πρέπει να είναι ίσο με ένα από τα  όπου
όπου  . Από την άλλη όμως
. Από την άλλη όμως  και
και  . Άρα,
. Άρα,  για κάθε
για κάθε  . Αν το
. Αν το  δεν είναι μονάδα (unit) τότε
δεν είναι μονάδα (unit) τότε  επειδή
επειδή  , δηλ.
, δηλ.  για κάποιο
για κάποιο  . Τότε, η
. Τότε, η  συνεπάγεται ότι
συνεπάγεται ότι  , το οποίο αντιβαίνει στο γεγονός ότι το
, το οποίο αντιβαίνει στο γεγονός ότι το  είναι μονάδα.
είναι μονάδα.
Καλημέρα. Λογικά, εννοείς, αμφίπλευρα ιδεώδη, οπότε δουλεύω με αυτά. Έστω το τυχόν
 , όπου
, όπου  . Για κάθε
. Για κάθε 
 και ταυτόχρονα
και ταυτόχρονα  (αφού
(αφού  ιδεώδη), άρα
ιδεώδη), άρα  και επειδή
και επειδή  υποομάδα του δακτυλίου με την πρόσθεση, παίρνουμε ότι
υποομάδα του δακτυλίου με την πρόσθεση, παίρνουμε ότι 
 .
. των ακέραιων αριθμών. Θέτουμε
των ακέραιων αριθμών. Θέτουμε  . Ως γνωστόν,
. Ως γνωστόν,  ενώ
ενώ ![I\cap J=4\,\mathbb{Z}\cap 6\,\mathbb{Z}=[4,6]\,\mathbb{Z}=12\,\mathbb{Z} I\cap J=4\,\mathbb{Z}\cap 6\,\mathbb{Z}=[4,6]\,\mathbb{Z}=12\,\mathbb{Z}](/forum/ext/geomar/texintegr/latexrender/pictures/461906223b5b995b35023757e30d0df8.png)
 ενώ
ενώ  .
.Υπόδειξη:
Όχι δεν αλλάζει κάτι. Θεώρησε τα ιδεώδη
 στον δακτύλιο
στον δακτύλιο  .
. είναι πρώτα, όμως
είναι πρώτα, όμως  και
και  , άρα πάλι έχουμε
, άρα πάλι έχουμε  .
.Υπόδειξη: Χρησιμοποιήστε τα θεωρήματα Sylow.
 .
. , ώστε να υπάρχουν τουλάχιστον τρεις μη ισομορφες ομάδες τάξης
, ώστε να υπάρχουν τουλάχιστον τρεις μη ισομορφες ομάδες τάξης  ;
;Έστω ομάδα
 με
με  . Για το πλήθος
. Για το πλήθος  των
των  -Sylow υποομάδων της
-Sylow υποομάδων της  ισχύει
ισχύει  και
και  , οπότε
, οπότε  , δηλαδή η
, δηλαδή η  έχει μοναδική υποομάδα τάξης
έχει μοναδική υποομάδα τάξης  , έστω
, έστω  . Με ίδιο σκεπτικό, υπάρχει μοναδική υποομάδα της
. Με ίδιο σκεπτικό, υπάρχει μοναδική υποομάδα της  τάξης
τάξης  , έστω
, έστω  . Συνεπώς,
. Συνεπώς,  . Μάλιστα
. Μάλιστα  . Ας παρατηρήσουμε ότι για οποιαδήποτε
. Ας παρατηρήσουμε ότι για οποιαδήποτε  ισχύει
ισχύει  . Πράγματι,
. Πράγματι,  (εδώ χρησιμοποιηθήκε το γεγονός ότι
(εδώ χρησιμοποιηθήκε το γεγονός ότι  κανονικές στη
κανονικές στη  ), άρα
), άρα  , όπως θέλαμε. Τώρα, ορίζουμε την απεικόνιση
, όπως θέλαμε. Τώρα, ορίζουμε την απεικόνιση  η οποία είναι μορφισμός ομάδων αφού
η οποία είναι μορφισμός ομάδων αφού  για κάθε
για κάθε  . Είναι μονομορφισμός διότι αν
. Είναι μονομορφισμός διότι αν  με
με  , τότε
, τότε 
 , οπότε η
, οπότε η  είναι και επί της
είναι και επί της  . Τελικά,
. Τελικά,  ισομορφισμός και συνεπώς
ισομορφισμός και συνεπώς 
Η δική μου η απόδειξη μοιάζει με τη δική σου πολύ.BAGGP93 έγραψε: ↑Τετ Νοέμ 11, 2020 10:30 pmΈστω ομάδαμε
. Για το πλήθος
των
-Sylow υποομάδων της
ισχύει
και
, οπότε
, δηλαδή η
έχει μοναδική υποομάδα τάξης
, έστω
. Με ίδιο σκεπτικό, υπάρχει μοναδική υποομάδα της
τάξης
, έστω
. Συνεπώς,
. Μάλιστα
. Ας παρατηρήσουμε ότι για οποιαδήποτε
ισχύει
. Πράγματι,
(εδώ χρησιμοποιηθήκε το γεγονός ότι
κανονικές στη
), άρα
, όπως θέλαμε. Τώρα, ορίζουμε την απεικόνιση
η οποία είναι μορφισμός ομάδων αφού
για κάθε
. Είναι μονομορφισμός διότι αν
με
, τότε
Επιπλέον, οπότε η
είναι και επί της
. Τελικά,
ισομορφισμός και συνεπώς

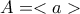 και
και  οι μοναδικές κυκλικές υποομάδες τάξεων 5 και 7.
οι μοναδικές κυκλικές υποομάδες τάξεων 5 και 7. . Βλέπουμε εύκολα ότι τα
. Βλέπουμε εύκολα ότι τα  . Άρα
. Άρα  και
και  ,άρα τελικά η τάξη του
,άρα τελικά η τάξη του 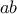 είναι 35.
είναι 35.Ωραίο. Πιο άμεσο.stranger έγραψε: ↑Τετ Νοέμ 11, 2020 10:39 pmΗ δική μου η απόδειξη μοιάζει με τη δική σου πολύ.BAGGP93 έγραψε: ↑Τετ Νοέμ 11, 2020 10:30 pmΈστω ομάδαμε
. Για το πλήθος
των
-Sylow υποομάδων της
ισχύει
και
, οπότε
, δηλαδή η
έχει μοναδική υποομάδα τάξης
, έστω
. Με ίδιο σκεπτικό, υπάρχει μοναδική υποομάδα της
τάξης
, έστω
. Συνεπώς,
. Μάλιστα
. Ας παρατηρήσουμε ότι για οποιαδήποτε
ισχύει
. Πράγματι,
(εδώ χρησιμοποιηθήκε το γεγονός ότι
κανονικές στη
), άρα
, όπως θέλαμε. Τώρα, ορίζουμε την απεικόνιση
η οποία είναι μορφισμός ομάδων αφού
για κάθε
. Είναι μονομορφισμός διότι αν
με
, τότε
Επιπλέον, οπότε η
είναι και επί της
. Τελικά,
ισομορφισμός και συνεπώς

Λέμε ότικαι
οι μοναδικές κυκλικές υποομάδες τάξεων 5 και 7.
Θα δείξουμε ότι. Βλέπουμε εύκολα ότι τα
. Άρα
και
,άρα τελικά η τάξη του
είναι 35.
Μπορούμε και πιο εύκολα να το αποδείξουμε. Έχουμε ότι για κάθε διαιρέτη
 του 35 υπάρχει μοναδική υποομάδα τάξης
του 35 υπάρχει μοναδική υποομάδα τάξης  .
. ένας μεταθετικός δακτύλιος με μονάδα, ώστε κάθε υποπρότυπο ενός ελεύθερου
ένας μεταθετικός δακτύλιος με μονάδα, ώστε κάθε υποπρότυπο ενός ελεύθερου  - προτύπου είναι ελεύθερο
- προτύπου είναι ελεύθερο  -πρότυπο.
-πρότυπο. είναι περιοχή κυρίων ιδεωδών.
είναι περιοχή κυρίων ιδεωδών.Τετριμμένο είναι.

 .
.
 στοιχεία και δύο ομάδες με
στοιχεία και δύο ομάδες με 
Δεν νομίζω ότι είναι δύσκολη.
 πρώτοι και
πρώτοι και  ομάδα με
ομάδα με 

 υπάρχει μοναδική ομάδα που είναι κυκλική
υπάρχει μοναδική ομάδα που είναι κυκλική τελειώσαμε.
τελειώσαμε. και στοιχείο τάξης
και στοιχείο τάξης 
 τότε οι ομάδα θα αποτελείτο από
τότε οι ομάδα θα αποτελείτο από  υποομάδες
υποομάδες  .
. κλπ ΑΤΟΠΟ.
κλπ ΑΤΟΠΟ.
 είναι κανονική γιατί απο τον τύπο του μετρήματος για υποομάδες
είναι κανονική γιατί απο τον τύπο του μετρήματος για υποομάδες 
 τάξης
τάξης 




 και είναι άμεσο ότι η ομάδα είναι κυκλική.
και είναι άμεσο ότι η ομάδα είναι κυκλική.Υπόδειξη: Ο
 είναι
είναι  -πρότυπο με εξωτερικό πολλαπλασιασμό το γινόμενο στον
-πρότυπο με εξωτερικό πολλαπλασιασμό το γινόμενο στον  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης