Ασκήσεις Άλγεβρας
Συντονιστής: Demetres
Re: Ασκήσεις Άλγεβρας
10) Δείξτε ότι κάθε ομάδα τάξης 1645 δεν είναι απλή.
Κωνσταντίνος Σμπώκος
Λέξεις Κλειδιά:
Re: Ασκήσεις Άλγεβρας
11) Έστω ένα σώμα  και μια επέκταση σωμάτων
και μια επέκταση σωμάτων  . Έστω
. Έστω  ένας δακτύλιος με
ένας δακτύλιος με 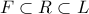 .
.
Δείξτε ότι ο είναι σώμα.
είναι σώμα.
edit: Η είναι αλγεβρική επέκταση.
είναι αλγεβρική επέκταση.
 και μια επέκταση σωμάτων
και μια επέκταση σωμάτων  . Έστω
. Έστω  ένας δακτύλιος με
ένας δακτύλιος με 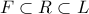 .
.Δείξτε ότι ο
 είναι σώμα.
είναι σώμα.edit: Η
 είναι αλγεβρική επέκταση.
είναι αλγεβρική επέκταση.
τελευταία επεξεργασία από stranger σε Σάβ Νοέμ 21, 2020 1:31 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Κωνσταντίνος Σμπώκος
Re: Ασκήσεις Άλγεβρας
Υπόδειξη:
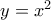 , τριώνυμο ως προς
, τριώνυμο ως προς  και έτσι βρίσκουμε τις ρίζες. Υπολογίζουμε τον βαθμό επέκτασης και λοιπα..
και έτσι βρίσκουμε τις ρίζες. Υπολογίζουμε τον βαθμό επέκτασης και λοιπα..Σχεδόν τυφλοσούρτης είναι..
Κωνσταντίνος Σμπώκος
-
bouzoukman
- Δημοσιεύσεις: 125
- Εγγραφή: Δευ Ιαν 19, 2009 7:53 pm
- Επικοινωνία:
Re: Ασκήσεις Άλγεβρας
Λοιπόν έχουμε ότι
 . Οπότε καταλαβαίνουμε ότι το splitting field του πολυωνύμου είναι το
. Οπότε καταλαβαίνουμε ότι το splitting field του πολυωνύμου είναι το  . Επειδή υπάρχουν μόνο δύο ομάδες τάξεως
. Επειδή υπάρχουν μόνο δύο ομάδες τάξεως  , οι
, οι  και
και  , καταλαβαίνουμε ότι στην περίπτωσή μας είμαστε στη 2η περίπτωση.
, καταλαβαίνουμε ότι στην περίπτωσή μας είμαστε στη 2η περίπτωση."Υπάρχει αρκετό φως γι' αυτούς που επιθυμούν να δουν και αρκετό σκοτάδι γι' αυτούς που έχουν την αντίθετη επιθυμία", B. Pascal
Re: Ασκήσεις Άλγεβρας
bouzoukman έγραψε: ↑Δευ Νοέμ 23, 2020 7:50 pmΛοιπόν έχουμε ότι. Οπότε καταλαβαίνουμε ότι το splitting field του πολυωνύμου είναι το
. Επειδή υπάρχουν μόνο δύο ομάδες τάξεως
, οι
και
, καταλαβαίνουμε ότι στην περίπτωσή μας είμαστε στη 2η περίπτωση.
Πρέπει να δικιολογηθεί ότι δεν είναι η
 .
.Έπεται από το ότι για κάθε αυτομορφισμό
 του σώματος ριζών ισχύει
του σώματος ριζών ισχύει  .
.Κωνσταντίνος Σμπώκος
-
bouzoukman
- Δημοσιεύσεις: 125
- Εγγραφή: Δευ Ιαν 19, 2009 7:53 pm
- Επικοινωνία:
Re: Ασκήσεις Άλγεβρας
Αν ήταν
 τότε από θεωρία Galois θα ξέραμε ότι υπάρχει μόνο ένα υπόσωμα τάξεως
τότε από θεωρία Galois θα ξέραμε ότι υπάρχει μόνο ένα υπόσωμα τάξεως  που δεν ισχύει μιας και έχουμε τουλάχιστον
που δεν ισχύει μιας και έχουμε τουλάχιστον  , τα
, τα 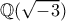 και
και  (η ουσία της απόδειξη είναι η ίδια με τη δικιά σου!).
(η ουσία της απόδειξη είναι η ίδια με τη δικιά σου!)."Υπάρχει αρκετό φως γι' αυτούς που επιθυμούν να δουν και αρκετό σκοτάδι γι' αυτούς που έχουν την αντίθετη επιθυμία", B. Pascal
Re: Ασκήσεις Άλγεβρας
bouzoukman έγραψε: ↑Δευ Νοέμ 23, 2020 9:30 pmΑν ήταντότε από θεωρία Galois θα ξέραμε ότι υπάρχει μόνο ένα υπόσωμα τάξεως
που δεν ισχύει μιας και έχουμε τουλάχιστον
, τα
και
(η ουσία της απόδειξη είναι η ίδια με τη δικιά σου!).
Κωνσταντίνος Σμπώκος
-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: Ασκήσεις Άλγεβρας
Το μόνο μη προφανές είναι ότι αν

εχει αντίστροφο.
Αφού το
 είναι αλγεβρικό επί του
είναι αλγεβρικό επί του  υπάρχει πολυώνυμο με συντελεστές
υπάρχει πολυώνυμο με συντελεστές από το
 και άρα από το
και άρα από το  με
με  .
.Παίρνουμε το ελαχίστου βαθμού.
Τότε

Εύκολα βλέπουμε ότι υπάρχει
 με με συντελεστές
με με συντελεστές από το
 και άρα από το
και άρα από το  ώστε
ώστε 
Αλλά είναι

και
 αρα υπάρχει αντίστροφο που ανήκει στο
αρα υπάρχει αντίστροφο που ανήκει στο 
οπότε και στο
 .
.Αρα

που δείχνει ότι το
 έχει αντίστροφο.
έχει αντίστροφο.Re: Ασκήσεις Άλγεβρας
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τρί Νοέμ 24, 2020 12:03 amΤο μόνο μη προφανές είναι ότι αν
εχει αντίστροφο.
Αφού τοείναι αλγεβρικό επί του
υπάρχει πολυώνυμο με συντελεστές
από τοκαι άρα από το
με
.
Παίρνουμε το ελαχίστου βαθμού.
Τότε
Εύκολα βλέπουμε ότι υπάρχειμε με συντελεστές
από τοκαι άρα από το
ώστε
Αλλά είναι
καιαρα υπάρχει αντίστροφο που ανήκει στο
οπότε και στο.
Αρα
που δείχνει ότι τοέχει αντίστροφο.
Ευχαριστούμε πολύ Σταύρο!ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Δευ Νοέμ 23, 2020 11:50 pmhttps://math.stackexchange.com/question ... q-r-primes

Έπεται και συνέχεια...
Κωνσταντίνος Σμπώκος
Re: Ασκήσεις Άλγεβρας
13) Δείξτε ότι κάθε ομάδα τάξης  , όπου
, όπου  περιττός πρώτος είναι επιλύσιμη.
περιττός πρώτος είναι επιλύσιμη.
 , όπου
, όπου  περιττός πρώτος είναι επιλύσιμη.
περιττός πρώτος είναι επιλύσιμη.Κωνσταντίνος Σμπώκος
Re: Ασκήσεις Άλγεβρας
Ἀσκηση 14 Αν  είναι προσεταιριστικός δακτύλιος με μονάδα, τότε να αποδείξετε ότι :\\
είναι προσεταιριστικός δακτύλιος με μονάδα, τότε να αποδείξετε ότι :\\
1. Υπάρχει μοναδικός μορφισμός δακτυλίων .
.
2. Υπάρχει το πολύ ένας ισομορφισμός δακτυλίων
3. Αν είναι δύο επιμορφισμοί δακτυλίων ώστε
είναι δύο επιμορφισμοί δακτυλίων ώστε 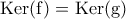 να δείξετε ότι
να δείξετε ότι  .
.
 είναι προσεταιριστικός δακτύλιος με μονάδα, τότε να αποδείξετε ότι :\\
είναι προσεταιριστικός δακτύλιος με μονάδα, τότε να αποδείξετε ότι :\\1. Υπάρχει μοναδικός μορφισμός δακτυλίων
 .
.2. Υπάρχει το πολύ ένας ισομορφισμός δακτυλίων

3. Αν
 είναι δύο επιμορφισμοί δακτυλίων ώστε
είναι δύο επιμορφισμοί δακτυλίων ώστε 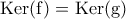 να δείξετε ότι
να δείξετε ότι  .
.Παπαπέτρος Ευάγγελος
Re: Ασκήσεις Άλγεβρας
1. Αν
 είναι ομομορφισμός τότε
είναι ομομορφισμός τότε  , οπότε υπάρχει μοναδικός ομομορφισμός μεταξύ τους.
, οπότε υπάρχει μοναδικός ομομορφισμός μεταξύ τους.2. Αν
 είναι ισομορφισμός, τότε η
είναι ισομορφισμός, τότε η  είναι 1-1 και επί. Επίσης εύκολα μπορούμε να δούμε ότι η
είναι 1-1 και επί. Επίσης εύκολα μπορούμε να δούμε ότι η  είναι ομομορφισμός. Άρα από το 1 έχουμε ότι αν
είναι ομομορφισμός. Άρα από το 1 έχουμε ότι αν  ισομορφισμοί από το
ισομορφισμοί από το  στο
στο  τότε
τότε  οπότε
οπότε  .
.3. Αν
 επιμορφισμοί με
επιμορφισμοί με  τότε οι απεικονίσεις
τότε οι απεικονίσεις  με
με  και
και  είναι ισομορφισμοί δακτυλίων, οπότε από το 2 έχουμε
είναι ισομορφισμοί δακτυλίων, οπότε από το 2 έχουμε  .
.Άρα
 και το συμπέρασμα έπεται.
και το συμπέρασμα έπεται.Κωνσταντίνος Σμπώκος
-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: Ασκήσεις Άλγεβρας
https://en.wikipedia.org/wiki/P-group
https://en.wikipedia.org/wiki/Solvable_group
Κάθε ομάδα με
 στοιχεία όπου
στοιχεία όπου  πρώτος και
πρώτος και  μη μηδενικός φυσικός είναι
μη μηδενικός φυσικός είναιεπιλύσιμη.
Στην συγκεκριμένη περίπτωση
(γιατί το
 δεν μπορεί να είναι
δεν μπορεί να είναι  δεν το καταλαβαίνω)
δεν το καταλαβαίνω) αρκεί να χρησιμοποιήσουμε ότι σε μια ομάδα με
 στοιχεία το κέντρο είναι μη τετριμμένο
στοιχεία το κέντρο είναι μη τετριμμένοκαι ότι μια ομάδα με
 είναι αβελιανή.
είναι αβελιανή.-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: Ασκήσεις Άλγεβρας
Όχι μόνο ένας μορφισμός υπάρχει.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Κυρ Δεκ 06, 2020 12:16 amΧάνω κάτι ;
Αν
δεν υπάρχουν αρκετοί ;
Ο μηδενικός δεν είναι μορφισμός ;
Θεώρησα ότι κάθε μορφισμός στέλνει το μοναδιαίο στοιχείο στο μοναδιαίο στοιχείο.
Πολλές φορές το υποθέτουμε αυτό όταν μιλάμε για μορφισμούς.
Κωνσταντίνος Σμπώκος
-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: Ασκήσεις Άλγεβρας
Εχεις δίκιο.stranger έγραψε: ↑Κυρ Δεκ 06, 2020 7:49 amΌχι μόνο ένας μορφισμός υπάρχει.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Κυρ Δεκ 06, 2020 12:16 amΧάνω κάτι ;
Αν
δεν υπάρχουν αρκετοί ;
Ο μηδενικός δεν είναι μορφισμός ;
Θεώρησα ότι κάθε μορφισμός στέλνει το μοναδιαίο στοιχείο στο μοναδιαίο στοιχείο.
Πολλές φορές το υποθέτουμε αυτό όταν μιλάμε για μορφισμούς.
https://en.wikipedia.org/wiki/Ring_homomorphism
Από την άλλη
https://el.wikipedia.org/wiki/%CE%9F%CE ... F%89%CE%BD
λέει τον ορισμό χωρίς μοναδιαίο.
Το ίδιο γίνεται και στο βιβλίο
Μια Εισαγωγή στην Αλγεβρα
Δ.Βαρσος -Δ.Δεριζιώτης κλπ
Κοιτάζοντας διάφορα βιβλία διαπίστωσα ότι τα Ελληνικά έχουν ορισμό χωρίς να απαιτούν που πάει το μοναδιαίο
ενω τα ξενόγλωσσα απαιτούν το μοναδιαίο να πηγαίνει σε μοναδιαίο.
Re: Ασκήσεις Άλγεβρας
Καλημέρα.
Ἀσκηση 15
Αν είναι μια ακέραια περιοχή, να αποδείξετε ότι η τομή όλων των μεγιστοτικών ιδεωδών στον πολυωνυμικό δακτύλιο
είναι μια ακέραια περιοχή, να αποδείξετε ότι η τομή όλων των μεγιστοτικών ιδεωδών στον πολυωνυμικό δακτύλιο ![R[x] R[x]](/forum/ext/geomar/texintegr/latexrender/pictures/c5b845aa2373916b6d15dbfe5ce5aae3.png) είναι το μηδενικό ιδεώδες.
είναι το μηδενικό ιδεώδες.
Ἀσκηση 15
Αν
 είναι μια ακέραια περιοχή, να αποδείξετε ότι η τομή όλων των μεγιστοτικών ιδεωδών στον πολυωνυμικό δακτύλιο
είναι μια ακέραια περιοχή, να αποδείξετε ότι η τομή όλων των μεγιστοτικών ιδεωδών στον πολυωνυμικό δακτύλιο ![R[x] R[x]](/forum/ext/geomar/texintegr/latexrender/pictures/c5b845aa2373916b6d15dbfe5ce5aae3.png) είναι το μηδενικό ιδεώδες.
είναι το μηδενικό ιδεώδες.Παπαπέτρος Ευάγγελος
Re: Ασκήσεις Άλγεβρας
Ναι και εγώ όταν πρωτοέμαθα βασική άλγεβρα διάβαζα το βιβλίο Μια εισαγωγή στην άλγεβρα των Βάρσου-Δεριζιώτη κλπ και εκεί δεν υποθέτουν όταν ένας μορφισμός στέλενει το μοναδιαίο στο μοναδιαίο. Μάλιστα στον ορισμό του δακτυλίου δεν υποθέτουν ότι το μοναδιαίο στοιχείο υπάρχει πάντα.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Κυρ Δεκ 06, 2020 10:25 amΕχεις δίκιο.stranger έγραψε: ↑Κυρ Δεκ 06, 2020 7:49 amΌχι μόνο ένας μορφισμός υπάρχει.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Κυρ Δεκ 06, 2020 12:16 amΧάνω κάτι ;
Αν
δεν υπάρχουν αρκετοί ;
Ο μηδενικός δεν είναι μορφισμός ;
Θεώρησα ότι κάθε μορφισμός στέλνει το μοναδιαίο στοιχείο στο μοναδιαίο στοιχείο.
Πολλές φορές το υποθέτουμε αυτό όταν μιλάμε για μορφισμούς.
https://en.wikipedia.org/wiki/Ring_homomorphism
Από την άλλη
https://el.wikipedia.org/wiki/%CE%9F%CE ... F%89%CE%BD
λέει τον ορισμό χωρίς μοναδιαίο.
Το ίδιο γίνεται και στο βιβλίο
Μια Εισαγωγή στην Αλγεβρα
Δ.Βαρσος -Δ.Δεριζιώτης κλπ
Κοιτάζοντας διάφορα βιβλία διαπίστωσα ότι τα Ελληνικά έχουν ορισμό χωρίς να απαιτούν που πάει το μοναδιαίο
ενω τα ξενόγλωσσα απαιτούν το μοναδιαίο να πηγαίνει σε μοναδιαίο.
Αργότερα στα μαθήματα άλγεβρας στο εξωτερικό πάντα υπέθεταν ότι ένας μορφισμός στέλνει το μοναδιαίο στοιχείο στο μοναδιαίο.
Κωνσταντίνος Σμπώκος
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες

 επί του
επί του  .
. είναι δύο επιμορφισμοί δακτυλίων ώστε
είναι δύο επιμορφισμοί δακτυλίων ώστε 