 τέτοιος ώστε
τέτοιος ώστε
Υπολογίστε τον πίνακα

Συντονιστής: Demetres
Αν ο πίνακας είναι ο
 τότε η πρώτη γραμμή της πρώτης εξίσωσης δίνει
τότε η πρώτη γραμμή της πρώτης εξίσωσης δίνει  και η πρώτη γραμμή της δεύτερης εξίσωσης δίνει
και η πρώτη γραμμή της δεύτερης εξίσωσης δίνει  . Άρα
. Άρα  . Όμοια
. Όμοια  .
.  , άρα
, άρα  , οπότε από την
, οπότε από την  βρίσκουμε
βρίσκουμε 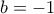 . Όμοια τα υπόλοιπα.
. Όμοια τα υπόλοιπα. έχει ιδιοτιμές
έχει ιδιοτιμές  με αντίστοιχα ιδιοδιανύσματα τα
με αντίστοιχα ιδιοδιανύσματα τα  . Επειδή το χαρακτηριστικό πολυώνυμο του
. Επειδή το χαρακτηριστικό πολυώνυμο του  είναι τρίτου βαθμού και έχουμε ήδη βρει τρεις
είναι τρίτου βαθμού και έχουμε ήδη βρει τρεις έπεται ότι
έπεται ότι 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες