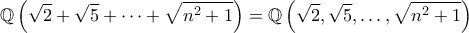
για όλους τους ακεραίους
 .
.Συντονιστής: Demetres
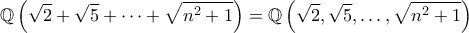
 .
.
 που δεν είναι τετράγωνα ακεραίων. Θα δείξουμε ότι
που δεν είναι τετράγωνα ακεραίων. Θα δείξουμε ότι  .
. είναι προφανής αφού
είναι προφανής αφού  .
. . Παρατηρούμε ότι:
. Παρατηρούμε ότι:


 .
. έπεται το ζητούμενο.
έπεται το ζητούμενο.
Μάρκος Βασίλης έγραψε: ↑Παρ Νοέμ 06, 2020 10:35 amΈστωπου δεν είναι τετράγωνα ακεραίων. Θα δείξουμε ότι
.
Ο ένας εγκλεισμός,είναι προφανής αφού
.
Για τον αντίστροφο εγκλεισμό, αρκεί να δείξουμε ότι. Παρατηρούμε ότι:
άρα:
και:
οπότε.
Τώρα, με επαγωγή στοέπεται το ζητούμενο.
με βάση την προηγούμενη απόδειξη δεν το βλέπω.
ΓιαΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Σάβ Νοέμ 07, 2020 4:59 pmΜάρκος Βασίλης έγραψε: ↑Παρ Νοέμ 06, 2020 10:35 amΈστωπου δεν είναι τετράγωνα ακεραίων. Θα δείξουμε ότι
.
Ο ένας εγκλεισμός,είναι προφανής αφού
.
Για τον αντίστροφο εγκλεισμό, αρκεί να δείξουμε ότι. Παρατηρούμε ότι:
άρα:
και:
οπότε.
Τώρα, με επαγωγή στοέπεται το ζητούμενο.
Αυτόμε βάση την προηγούμενη απόδειξη δεν το βλέπω.
Μήπως μπορείς να το εξηγήσεις ;
 είναι υποπερίπτωση του παραπάνω. Έστω ότι ισχύει για κάποιο
είναι υποπερίπτωση του παραπάνω. Έστω ότι ισχύει για κάποιο  . Τώρα μένει να δείξουμε ότι:
. Τώρα μένει να δείξουμε ότι:
 είναι άμεσος. Για τον εγκλεισμό
είναι άμεσος. Για τον εγκλεισμό  αρκεί να δείξουμε ότι
αρκεί να δείξουμε ότι  για
για  . Για
. Για  έχουμε πράγματι
έχουμε πράγματι  , ενώ για
, ενώ για  από την επαγωγική υπόθεση έχουμε:
από την επαγωγική υπόθεση έχουμε:
 .
.
Ισως να μην βλέπω κάτι αλλά νομίζω ότι πρέπει να δειχθεί ότιΜάρκος Βασίλης έγραψε: ↑Κυρ Νοέμ 08, 2020 12:42 amΓιαΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Σάβ Νοέμ 07, 2020 4:59 pmΜάρκος Βασίλης έγραψε: ↑Παρ Νοέμ 06, 2020 10:35 amΈστωπου δεν είναι τετράγωνα ακεραίων. Θα δείξουμε ότι
.
Ο ένας εγκλεισμός,είναι προφανής αφού
.
Για τον αντίστροφο εγκλεισμό, αρκεί να δείξουμε ότι. Παρατηρούμε ότι:
άρα:
και:
οπότε.
Τώρα, με επαγωγή στοέπεται το ζητούμενο.
Αυτόμε βάση την προηγούμενη απόδειξη δεν το βλέπω.
Μήπως μπορείς να το εξηγήσεις ;είναι υποπερίπτωση του παραπάνω. Έστω ότι ισχύει για κάποιο
. Τώρα μένει να δείξουμε ότι:
Ο εγκλεισμόςείναι άμεσος. Για τον εγκλεισμό
αρκεί να δείξουμε ότι
για
. Για
έχουμε πράγματι
, ενώ για
από την επαγωγική υπόθεση έχουμε:
άρα.

Πολύ σωστά, μάλλον ήταν αργά εχθές όταν το έγραφα αυτό, ευχαριστώ για την επισήμανση!ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Κυρ Νοέμ 08, 2020 9:48 amΙσως να μην βλέπω κάτι αλλά νομίζω ότι πρέπει να δειχθεί ότι

 είναι προφανής. Όσο για τον αντίστροφο, θα τον συμπληρώσω μέσα στη μέρα.
είναι προφανής. Όσο για τον αντίστροφο, θα τον συμπληρώσω μέσα στη μέρα.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες