Παραθετω μια προσέγγιση. Ελπίζω να μην μου έχει φύγει κάτι.
Έστω
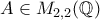
και

ένας θετικός μη τετράγωνος ρητός. Το χαρακτηριστικό πολυώνυμο του

είναι

. Αν θεωρήσουμε τον

ως πίνακα του

το χαρακτηριστικό πολυώνυμο παραμένει το ίδιο και έχει ρίζες

που ενδεχομένως είναι ίσες.
Αν υποτεθεί ότι

τότε έχουμεQ

Επομένως
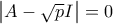
ή

άρα κάποιοις από τους

είναι ιδιοτιμή του

και επομένως ρίζα του

.
Για τα

διακρίνουμε τις εξής περιπτώσεις:
ΠΕΡ 1.

ΠΕΡ 2.
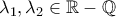
ΠΕΡ 3.

H πρώτη περίπτωση αποκλείεται αφού κάποιος από τους

πρέπει να είναι

.
Η τρίτη περίπτωση αποκλείεται διότι κάποιος από τους ρητούς

πρέπει να είναι ίσος με κάποιοςν από τους άρρητους

.
Απομένει η δεύτερη περίπτωση. Επειδή το

έχει ρητούς συντελεστές αν δέχεται ως ρίζα κάποιον από τους

θα δέχεται και τον συζυγή του. Άρα

. Άρα ο

έχει δύο διαφορετικές ιδιοτιμές και επομένως είναι διαγωνιοποιήσιμος δηλαδή υπάρχει
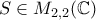
ώστε

όπου

με
![\displaystyle D = \left[ {\begin{array}{*{20}{c}}
{{\lambda _1}}&0\\
0&{{\lambda _2}}
\end{array}} \right] \displaystyle D = \left[ {\begin{array}{*{20}{c}}
{{\lambda _1}}&0\\
0&{{\lambda _2}}
\end{array}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/d3474d100b1e4c509761e32f3c45298f.png)
.
Τότε

και επομένως ο

είναι ο βαθμωτός πίνακας

αντιμετατίθεται με όλους τους πίνακες.
Από αυτό προκύπτει το πρώτο ερώτημα.
Σκεφτομενοι ανάλογα για τον  έχουμε και το δεύτερο ερώτημα.
έχουμε και το δεύτερο ερώτημα.
Θα. με ενδιέφερε να μάθω την προέλευση της άσκησης και αν γίνεται και την προτεινόμενη λύση.
Edit Από αβλεψία μου διάβασα λάθος την εκφώνηση και την εξέλαβα ως

.
Επομένως δεν έχω δώσει απάντηση στο ερώτημα. Ευχαριστώ πολύ τον Δημήτρη Χριστοφίδη που ευγενικά μου επεσήμανε με pm την αβλεψία μου.
 πίνακες τέτοιοι ώστε
πίνακες τέτοιοι ώστε όπου
όπου 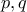 πρώτοι αριθμοί.
πρώτοι αριθμοί. πίνακες τέτοιοι ώστε
πίνακες τέτοιοι ώστε όπου
όπου 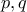 πρώτοι αριθμοί.
πρώτοι αριθμοί. ,
,  .
. ,
,  .
. να είναι μη τετράγωνος ρητός.
να είναι μη τετράγωνος ρητός.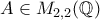 και
και  είναι
είναι  . Αν θεωρήσουμε τον
. Αν θεωρήσουμε τον  το χαρακτηριστικό πολυώνυμο παραμένει το ίδιο και έχει ρίζες
το χαρακτηριστικό πολυώνυμο παραμένει το ίδιο και έχει ρίζες  που ενδεχομένως είναι ίσες.
που ενδεχομένως είναι ίσες.  τότε έχουμεQ
τότε έχουμεQ
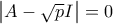 ή
ή  άρα κάποιοις από τους
άρα κάποιοις από τους  είναι ιδιοτιμή του
είναι ιδιοτιμή του  .
.
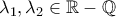

 θα δέχεται και τον συζυγή του. Άρα
θα δέχεται και τον συζυγή του. Άρα  . Άρα ο
. Άρα ο  έχει δύο διαφορετικές ιδιοτιμές και επομένως είναι διαγωνιοποιήσιμος δηλαδή υπάρχει
έχει δύο διαφορετικές ιδιοτιμές και επομένως είναι διαγωνιοποιήσιμος δηλαδή υπάρχει 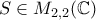 ώστε
ώστε  όπου
όπου ![\displaystyle D = \left[ {\begin{array}{*{20}{c}}
{{\lambda _1}}&0\\
0&{{\lambda _2}}
\end{array}} \right] \displaystyle D = \left[ {\begin{array}{*{20}{c}}
{{\lambda _1}}&0\\
0&{{\lambda _2}}
\end{array}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/d3474d100b1e4c509761e32f3c45298f.png) .
.
 είναι ο βαθμωτός πίνακας
είναι ο βαθμωτός πίνακας  αντιμετατίθεται με όλους τους πίνακες.
αντιμετατίθεται με όλους τους πίνακες. έχουμε και το δεύτερο ερώτημα.
έχουμε και το δεύτερο ερώτημα. .
.  όχι τετράγωνο ρητού. Θα είναι όπως πριν
όχι τετράγωνο ρητού. Θα είναι όπως πριν  . Αν επιπλέον το γινόμενο
. Αν επιπλέον το γινόμενο 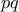 δεν είναι τετράγωνο ρητού (λ.χ. όταν οι
δεν είναι τετράγωνο ρητού (λ.χ. όταν οι 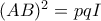 . Άρα
. Άρα  οπότε
οπότε 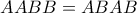 . Αλλά οι
. Αλλά οι  έχουν μη μηδενική ορίζουσα και επομένως είναι αντιστρέψιμοι. Άρα
έχουν μη μηδενική ορίζουσα και επομένως είναι αντιστρέψιμοι. Άρα  . Αυτό μας δίνει το (i). Χρωστάω το ii).
. Αυτό μας δίνει το (i). Χρωστάω το ii). .
.  .
. είναι το
είναι το  και από την υπόθεση
και από την υπόθεση 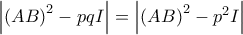 έχει ρίζα την ιδιοτιμή
έχει ρίζα την ιδιοτιμή  του
του  . Άρα
. Άρα  οπότε
οπότε  που σημαίνει ότι το χαρακτηριστικό πολυώνυμο του
που σημαίνει ότι το χαρακτηριστικό πολυώνυμο του  . Επομένως από το θεώρημα Cayley-Hamilton έχουμε:
. Επομένως από το θεώρημα Cayley-Hamilton έχουμε:
 και
και 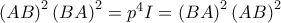
 ,
, 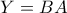 και έχουμε:
και έχουμε:
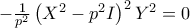
 λόγω της
λόγω της  .
.
