Φαντάζομαι θα το διδάχτηκαν και στο μάθημα, σωστά; Διότι μπορεί το κάθε βήμα της απόδειξης που ξέρω να μην είναι δύσκολο αλλά να τα βάλεις όλα μαζί χωρίς να τα έχεις ξαναδεί εν ώρα εξετάσεων νομίζω είναι δύσκολο.
Έστω

το ελάχιστο πολυώνυμο του

.
Για

, τα

στοιχεία
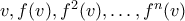
του

είναι ασφαλώς γραμμικώς εξαρτημένα. Άρα υπάρχει μοναδικό μονικό πολυώνυμο

ελάχιστου βαθμού ώστε

. Επειδή
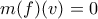
πρέπει

.
Από όλα τα πολυώνυμα

παίρνουμε ένα μέγιστου βαθμού, έστω το

. Αρκεί να δείξουμε ότι

αφού τότε δεν θα υπάρχει πολυώνυμο

βαθμού μικρότερου του

ώστε

, και άρα τα

θα είναι γραμμικώς ανεξάρτητα.
Για να δείξουμε το τελευταίο αρκεί να δείξουμε ότι

για κάθε

. Πράγματι τότε θα έχουμε
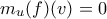
για κάθε

. Άρα

. Αφού επίσης

και τα δύο πολυώνυμα είναι μονικά, τότε όντως

.
Ας υποθέσουμε λοιπόν ότι υπάρχει

ώστε

. Μπορώ να βρω μονικά πολυώνυμα

πρώτα μεταξύ τους ώστε

και

, όπου
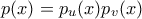
. (Απλό αν γράψουμε τα

ως γινόμενα ανάγωγων πολυωνύμων.)
Έστω

και
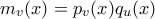
. Θέτω
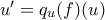
και

. Τότε

Επίσης δεν υπάρχει πολυώνυμο

μικρότερου βαθμού από το

με

αφού τότε θα είχαμε

που αντιβαίνει στο ότι το

είναι το ελάχιστο πολυώνυμο του

σε σχέση με το

. Ομοίως, το

είναι το ελάχιστο πολυώνυμο του

σε σχέση με το

.
Θέτω τώρα
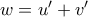
και παρατηρώ ότι
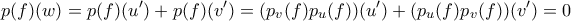
όπου στην πρώτη ισότητα χρησιμοποιήσαμε ότι η

είναι γραμμική.
Ισχυρίζομαι τώρα ότι

. Αυτό θα ολοκληρώσει την απόδειξη αφού το

έχει μεγαλύτερο βαθμό από το

. Έστω λοιπόν ότι αυτό δεν ισχύει. Έστω

το ελάχιστο κοινό πολλαπλάσιο των

και ορίζω το

ομοίως. Ένα από τα

θα έχει μικρότερο βαθμό από το

. Έστω το

. Τότε

αφού

και

.
Τότε όμως πρέπει

και άρα

. Επειδή επιπλέον

και

πρώτα μεταξύ τους, τότε

. Αυτό είναι άτοπο αφού υποθέσαμε ότι το

έχει μικρότερο βαθμό από το

.
Η απόδειξη ολοκληρώθηκε. Δεν γνωρίζω αν υπάρχει κάτι πιο σύντομο.
 γραμμικὸς χῶρος διαστάσεως
γραμμικὸς χῶρος διαστάσεως  ἐπί τοῦ σώματος
ἐπί τοῦ σώματος  καὶ
καὶ  γραμμικὴ ἀπεικόνιση. Ἄν τὸ ἐλάχιστο πολυώνυμο τῆς
γραμμικὴ ἀπεικόνιση. Ἄν τὸ ἐλάχιστο πολυώνυμο τῆς  εἶναι βαθμοῦ
εἶναι βαθμοῦ  (ὅπου
(ὅπου  ), δείξατε ὅτι ὑπάρχει
), δείξατε ὅτι ὑπάρχει  , ὥστε τὰ στοιχεῖα
, ὥστε τὰ στοιχεῖα

 το ελάχιστο πολυώνυμο του
το ελάχιστο πολυώνυμο του  , τα
, τα  στοιχεία
στοιχεία 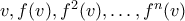 του
του  είναι ασφαλώς γραμμικώς εξαρτημένα. Άρα υπάρχει μοναδικό μονικό πολυώνυμο
είναι ασφαλώς γραμμικώς εξαρτημένα. Άρα υπάρχει μοναδικό μονικό πολυώνυμο  ελάχιστου βαθμού ώστε
ελάχιστου βαθμού ώστε  . Επειδή
. Επειδή 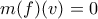 πρέπει
πρέπει  .
.  παίρνουμε ένα μέγιστου βαθμού, έστω το
παίρνουμε ένα μέγιστου βαθμού, έστω το  . Αρκεί να δείξουμε ότι
. Αρκεί να δείξουμε ότι  αφού τότε δεν θα υπάρχει πολυώνυμο
αφού τότε δεν θα υπάρχει πολυώνυμο  βαθμού μικρότερου του
βαθμού μικρότερου του  , και άρα τα
, και άρα τα  θα είναι γραμμικώς ανεξάρτητα.
θα είναι γραμμικώς ανεξάρτητα. για κάθε
για κάθε 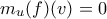 για κάθε
για κάθε  . Αφού επίσης
. Αφού επίσης  και τα δύο πολυώνυμα είναι μονικά, τότε όντως
και τα δύο πολυώνυμα είναι μονικά, τότε όντως  . Μπορώ να βρω μονικά πολυώνυμα
. Μπορώ να βρω μονικά πολυώνυμα  πρώτα μεταξύ τους ώστε
πρώτα μεταξύ τους ώστε  και
και  , όπου
, όπου 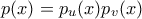 . (Απλό αν γράψουμε τα
. (Απλό αν γράψουμε τα  ως γινόμενα ανάγωγων πολυωνύμων.)
ως γινόμενα ανάγωγων πολυωνύμων.) και
και 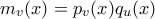 . Θέτω
. Θέτω 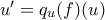 και
και  . Τότε
. Τότε 
 μικρότερου βαθμού από το
μικρότερου βαθμού από το  με
με  αφού τότε θα είχαμε
αφού τότε θα είχαμε
 σε σχέση με το
σε σχέση με το  είναι το ελάχιστο πολυώνυμο του
είναι το ελάχιστο πολυώνυμο του  σε σχέση με το
σε σχέση με το 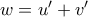 και παρατηρώ ότι
και παρατηρώ ότι 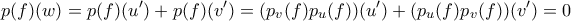
 . Αυτό θα ολοκληρώσει την απόδειξη αφού το
. Αυτό θα ολοκληρώσει την απόδειξη αφού το  έχει μεγαλύτερο βαθμό από το
έχει μεγαλύτερο βαθμό από το  το ελάχιστο κοινό πολλαπλάσιο των
το ελάχιστο κοινό πολλαπλάσιο των  και ορίζω το
και ορίζω το  ομοίως. Ένα από τα
ομοίως. Ένα από τα  θα έχει μικρότερο βαθμό από το
θα έχει μικρότερο βαθμό από το 
 και
και  .
. και άρα
και άρα  . Επειδή επιπλέον
. Επειδή επιπλέον  . Αυτό είναι άτοπο αφού υποθέσαμε ότι το
. Αυτό είναι άτοπο αφού υποθέσαμε ότι το 
 ἀνάγωγα ἐπὶ τοῦ
ἀνάγωγα ἐπὶ τοῦ  , ὥστε
, ὥστε  ,
, 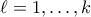 . Κατόπιν μέσω τῶν
. Κατόπιν μέσω τῶν  ὁρίζομε
ὁρίζομε  , ὥστε
, ὥστε  , καὶ ἐν τέλει τὸ στοιχεῖο
, καὶ ἐν τέλει τὸ στοιχεῖο
 ειναι ομοιος με
ειναι ομοιος με  ευθυ αθροισμα συνοδων πινακων οπου το πολυωνυμο
ευθυ αθροισμα συνοδων πινακων οπου το πολυωνυμο 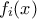 διαιρει το
διαιρει το  για κάθε
για κάθε  , τότε το ελαχιστο πολυώνυμο του
, τότε το ελαχιστο πολυώνυμο του  και μια επιλογη για το
και μια επιλογη για το  , οπου
, οπου 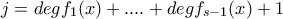 .
.