ΠινακοΠραξεις

nonlinear · #1

Έστω ο πίνακας $\displaystyle{A \in {{\rm M}_4}\left( R \right)}$ με την ιδιότητα $\displaystyle{{A^4} = {{\rm O}}}$ να δείξετε οτι υπάρχει πίνακας $\displaystyle{B \in {{\rm M}_4}\left( R \right)}$ ώστε $\displaystyle{{\left( {{I_4} + A} \right)^3} = {B^2}}$ .

(I,O μοναδιαίος ,μηδενικός αντίστοιχης τάξης)

Edit Διορθώθηκε η δύναμη του μηδενοπινακα

#2

nonlinear έγραψε:Έστω ο πίνακας $\displaystyle{A \in {{\rm M}_4}\left( R \right)}$ με την ιδιότητα $\displaystyle{{A^4} = {{\rm O}}}$ να δείξετε οτι υπάρχει πίνακας $\displaystyle{B \in {{\rm M}_4}\left( R \right)}$ ώστε $\displaystyle{{\left( {{I_4} + A} \right)^3} = {B^2}}$ .

(I,O μοναδιαίος ,μηδενικός αντίστοιχης τάξης)

Edit Διορθώθηκε η δύναμη του μηδενοπινακα

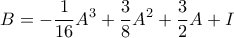Ο $\displaystyle{B=-\frac{1}{16}A^3+\frac{3}{8}A^2+\frac{3}{2}A+I}$ ικανοποιεί τη ζητούμενη σχέση.

Ο παραπάνω πίνακας βρέθηκε, αναζητώντας τον υπό τη μορφή $\displaystyle{B=xA^3+yA^2+zA+I}$ και κάνοντας χρήση των $\displaystyle{A^4=0}$ και $\displaystyle{B^2=A^3+3A^2+3A+I.}$

Σημειωτέον ότι δε χρησιμοποιήθηκε η διάσταση του πίνακα $\displaystyle{A}$ .

#3

Να προσθέσω ότι μετά την λύση του Θάνου βλέπουμε πως η άσκηση γενικεύεται και σε δακτυλίους:

Δίνεται ένας δακτύλιος

και ένα στοιχείο

με

. Τότε υπάρχει $y \in R$ ώστε (1+x)^3 = y^2

.

Ακόμη πιο γενικά: Δίνεται ένας δακτύλιος

, θετικοί ακέραιοι m,n

, πολυώνυμο

με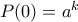

για κάποιο $a \in \mathbb{Z} \setminus \{0\}$ και ένα στοιχείο $x \in R$ με x^m = 0

. Να δειχθεί ότι υπάρχει $y \in R$ ώστε P(x) = y^k

ΠινακοΠραξεις

ΠινακοΠραξεις

Re: ΠινακοΠραξεις

Re: ΠινακοΠραξεις

Μέλη σε σύνδεση