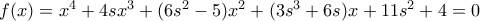 , όπου
, όπου  . Η εξίσωση έχει τέσσερεις άνισες πραγματικές ρίζες και το άθροισμα δύο ριζών της είναι ίσο με το άθροισμα των άλλων δύο ριζών της.
. Η εξίσωση έχει τέσσερεις άνισες πραγματικές ρίζες και το άθροισμα δύο ριζών της είναι ίσο με το άθροισμα των άλλων δύο ριζών της.α) Να βρεθούν οι δυνατές τιμές του
 .
.β) Να βρεθούν οι ρίζες του
 για κάθε δυνατή τιμή του
για κάθε δυνατή τιμή του  .
.Συντονιστής: Demetres
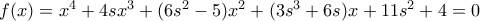 , όπου
, όπου  . Η εξίσωση έχει τέσσερεις άνισες πραγματικές ρίζες και το άθροισμα δύο ριζών της είναι ίσο με το άθροισμα των άλλων δύο ριζών της.
. Η εξίσωση έχει τέσσερεις άνισες πραγματικές ρίζες και το άθροισμα δύο ριζών της είναι ίσο με το άθροισμα των άλλων δύο ριζών της. .
. για κάθε δυνατή τιμή του
για κάθε δυνατή τιμή του  .
.Δεν νομίζω ότι είναι άσκηση για Άλγεβρα Α.Ε.Ι. καθώς είναι μία μάλλον απλή άσκηση σε Vieta.DreamingMaths έγραψε: ↑Τρί Μάιος 31, 2022 9:28 pmΔίνεται η εξίσωση, όπου
. Η εξίσωση έχει τέσσερεις άνισες πραγματικές ρίζες και το άθροισμα δύο ριζών της είναι ίσο με το άθροισμα των άλλων δύο ριζών της.
α) Να βρεθούν οι δυνατές τιμές του.
β) Να βρεθούν οι ρίζες τουγια κάθε δυνατή τιμή του
.
 οι ρίζες με
οι ρίζες με 
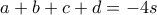 , οπότε
, οπότε 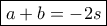
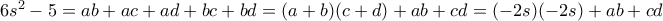 , άρα
, άρα 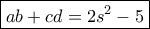 .
.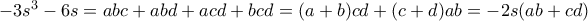 . Άρα είτε
. Άρα είτε  ή
ή 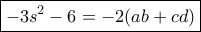 .
.  . Τότε η αρχική είναι
. Τότε η αρχική είναι 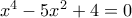 με ρίζες
με ρίζες  (δεκτές αφού
(δεκτές αφού  ).
).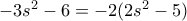 , άρα
, άρα 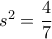 .
. 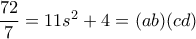
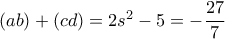 βρίσκουμε τα
βρίσκουμε τα 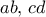 . Είναι οι μιγαδικοί
. Είναι οι μιγαδικοί 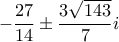 . Αν δεν θέλουμε μιγαδικούς, σταματάμε. Αλλιώς,
. Αν δεν θέλουμε μιγαδικούς, σταματάμε. Αλλιώς, 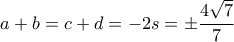 βρίσκουμε τα
βρίσκουμε τα  και ελέγχουμε. Δεν αξίζει τον κόπο να γίνουν οι πράξεις.
και ελέγχουμε. Δεν αξίζει τον κόπο να γίνουν οι πράξεις. είναι να το αντιπαταστήσουμε πίσω στην αρχική και μετά να λύσουμε την τεταρτοβάθμια. Η τεχνική είναι γνωστή και δεν υπάρχει λόγος να ξανακάνω εδώ βήματα ρουτίνας.
είναι να το αντιπαταστήσουμε πίσω στην αρχική και μετά να λύσουμε την τεταρτοβάθμια. Η τεχνική είναι γνωστή και δεν υπάρχει λόγος να ξανακάνω εδώ βήματα ρουτίνας.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες