 και
και 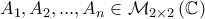 οι λύσεις της εξίσωσης
οι λύσεις της εξίσωσης 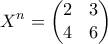 . Να δειχθεί ότι
. Να δειχθεί ότι  .
.Συντονιστής: Demetres
 και
και 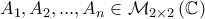 οι λύσεις της εξίσωσης
οι λύσεις της εξίσωσης 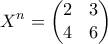 . Να δειχθεί ότι
. Να δειχθεί ότι  .
.
α) Ένας τρόπος είναι να κάνουμε διαγωνοποίηση του δεξιού μέλους. Με την στάνταρ διαδικασία ιδιοτιμών βρίσκουμε
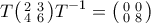 όπου
όπου  για τον οποίο
για τον οποίο 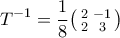
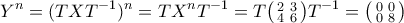 ,
,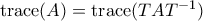 .
. (η δεύτερη στήλη είναι πολλαπλάσιο της πρώτης) από όπου εύκολα διαπιστώνουμε ότι
(η δεύτερη στήλη είναι πολλαπλάσιο της πρώτης) από όπου εύκολα διαπιστώνουμε ότι 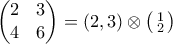
 πρέπει να είναι και αυτό τάξης
πρέπει να είναι και αυτό τάξης  (γιατί αν ήταν
(γιατί αν ήταν  θα ήταν επί οπότε θα ήταν επί και το
θα ήταν επί οπότε θα ήταν επί και το 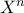 , που δεν είναι αφού το ίσο του είναι τάξης
, που δεν είναι αφού το ίσο του είναι τάξης  ). Γράφουμε λοιπόν
). Γράφουμε λοιπόν 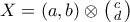 .
.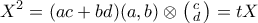 και επαγωγικά
και επαγωγικά 
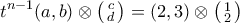
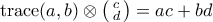 (γνωστό), παίρνοντας trace της πρηγούμενης γίνεται
(γνωστό), παίρνοντας trace της πρηγούμενης γίνεται 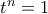 .
. 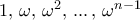 , όπου
, όπου  μιγαδική
μιγαδική  ρίζα της μονάδας. Άρα η τυπική λύση της αρχικής είναι
ρίζα της μονάδας. Άρα η τυπική λύση της αρχικής είναι 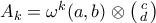
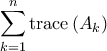 είναι πολλαπλάσιο του
είναι πολλαπλάσιο του 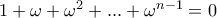 , όπως θέλαμε.
, όπως θέλαμε. .
.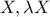 είναι δύο λύσεις, τότε το
είναι δύο λύσεις, τότε το  είναι νιοστή ρίζα της μονάδας. (Θεωρώ
είναι νιοστή ρίζα της μονάδας. (Θεωρώ 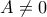 .) Άρα οι νιοστές ρίζες του
.) Άρα οι νιοστές ρίζες του  έρχονται σε
έρχονται σε  -άδες της μορφής
-άδες της μορφής  όπου
όπου 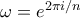 . Σε κάθε
. Σε κάθε  -άδα το άθροισμα των ιχνών είναι 0 αφού
-άδα το άθροισμα των ιχνών είναι 0 αφού 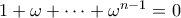 .
. .)
.) νιοστές ρίζες αφού αυτό δίνεται στην εκφώνηση. Οπότε τελειώσαμε.
νιοστές ρίζες αφού αυτό δίνεται στην εκφώνηση. Οπότε τελειώσαμε.  νιοστές ρίζες.)
νιοστές ρίζες.)Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 10 επισκέπτες