 τέτοιες ώστε
τέτοιες ώστε 
Συντονιστές: achilleas, emouroukos, silouan
 τέτοιες ώστε
τέτοιες ώστε 
 έχουμε
έχουμε  και άρα αν
και άρα αν  θα έχουμε
θα έχουμε  . Και από εκεί και πέρα με την τελευταία αντικατάσταση που έκανες παίρνουμε και την δεύτερη λύση της συναρτησιακής.
. Και από εκεί και πέρα με την τελευταία αντικατάσταση που έκανες παίρνουμε και την δεύτερη λύση της συναρτησιακής.Πώς ακριβώς βγαίνει αυτό; Πρώτα από όλα μάλλον εννοείςthrassos έγραψε:γιαέχουμε

 , αλλά το ερώτημα είναι πώς βγήκε η παράσταση ίση με
, αλλά το ερώτημα είναι πώς βγήκε η παράσταση ίση με 
 έπρεπε να είναι
έπρεπε να είναι  .
. αφού
αφού 
Και αυτό από που προκύπτει; Αυτό που βλέπω να προκύπτει είναι τοthrassos έγραψε: αφού

 .
. .
. θα προκύψει
θα προκύψει  (1).
(1). παίρνουμε ότι
παίρνουμε ότι  και από την (1) η τελευταία γίνεται
και από την (1) η τελευταία γίνεται 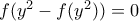 (2).
(2). τέτοιο ώστε
τέτοιο ώστε  .
. η αρχική γίνεται
η αρχική γίνεται  .
. η αρχική ,τώρα , γίνεται
η αρχική ,τώρα , γίνεται  ισοδύναμα
ισοδύναμα  .
. ή
ή  .
.  τότε
τότε  και άρα από την (1) και την (2) θα πάρουμε την άλλη λύση ,
και άρα από την (1) και την (2) θα πάρουμε την άλλη λύση ,  .
. τέτοιες ώστε
τέτοιες ώστε 
 τότε πρέπει
τότε πρέπει  και ότι αν
και ότι αν  τότε
τότε  .
.  τότε για
τότε για  παίρνουμε
παίρνουμε 
 έχουμε άτοπο. Επομένως
έχουμε άτοπο. Επομένως  για κάθε
για κάθε  .
.  παίρνουμε
παίρνουμε  . Αν τώρα
. Αν τώρα  έχουμε ότι
έχουμε ότι  . Αν θέλουμε τώρα
. Αν θέλουμε τώρα  δηλαδή
δηλαδή  τότε
τότε  , δηλαδή
, δηλαδή  για κάθε
για κάθε  . Επεκτείναμε δηλαδή το διάστημα που ισχύει η
. Επεκτείναμε δηλαδή το διάστημα που ισχύει η  .
. για κάθε
για κάθε 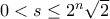 . Αφού ισχύει για κάθε
. Αφού ισχύει για κάθε  , έχουμε ότι
, έχουμε ότι  για κάθε
για κάθε  .
.silouan έγραψε:Αυτή μου φάνηκε πιο δύσκολη, εκτός αν χάνω κάτι. Βάζω τα βασικά βήματα τα οποία αφήνω προς απόδειξη για να ασχοληθεί περισσότερο κάποιος με την άσκηση. Αν εντοπιστεί κάποιο λάθος πείτε μου.
Βήμα 1: Δείχνουμε ότι αντότε πρέπει
και ότι αν
τότε
.
Βήμα 2: Έστωτότε για
παίρνουμε

και από το Βήμα 1 δείχνουμε ότι ανέχουμε άτοπο. Επομένως
για κάθε
.
Βήμα 3: Γιαπαίρνουμε
. Αν τώρα
έχουμε ότι
. Αν θέλουμε τώρα
δηλαδή
τότε
, δηλαδή
για κάθε
. Επεκτείναμε δηλαδή το διάστημα που ισχύει η
.
Με επαγωγή και όμοια με παραπάνω δείχνουμε ότιγια κάθε
. Αφού ισχύει για κάθε
, έχουμε ότι
για κάθε
.
 τότε
τότε 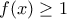 (δεν επηρεάζει βέβαια τη λύση πιο κάτω)
(δεν επηρεάζει βέβαια τη λύση πιο κάτω) για κάθε
για κάθε 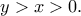 Αν θεωρήσουμε
Αν θεωρήσουμε  τότε
τότε  και για
και για  τελικά
τελικά 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες