Καλησπέρα κύριε Ανδρέα.Ανδρέας Πούλος έγραψε: ↑Δευ Φεβ 05, 2018 8:20 pm18η Άσκηση.
Σε μια ευθεία ορίζουμε δύο σημείακαι
.
Στη συνέχει επιλέγουμε τυχαία στην ευθεία 9 σημεία που δεν ανήκουν στο ευθύγραμμο τμήμα.
Να αποδείξετε ότι το άθροισμα των αποστάσεων των εννέα σημείων από το, δεν είναι ίσο με το άθροισμα των αποστάσεών τους από το
.
Αν γενικεύσετε το ερώτημα με, τι τιμές παίρνει ο φυσικός
ώστε να ισχύει το ζητούμενο;
Θα εργαστούμε κατευθείαν για την γενική περίπτωση.
Θα βρούμε για ποιες τιμές του
 μπορεί να είναι
μπορεί να είναι 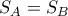 (όπου
(όπου 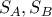 τα αθροίσματα των αποστάσεων των
τα αθροίσματα των αποστάσεων των  σημείων από τα
σημείων από τα  ).
).Ονομάζουμε
 τα σημεία.
τα σημεία.Έστω πως
 σημεία (έστω τα
σημεία (έστω τα  ) βρίσκονται αριστερά του
) βρίσκονται αριστερά του  , και τα υπόλοιπα
, και τα υπόλοιπα  (έστω τα
(έστω τα  ) δεξιά του
) δεξιά του  .
. Είναι
 .
.Όμοια
 .
. Είναι
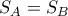 , άρα
, άρα  (1).
(1).Παρατηρούμε ότι για κάθε σημείο αριστερά του
 ισχύει
ισχύει  , ενώ για κάθε σημείο δεξιά του
, ενώ για κάθε σημείο δεξιά του  ισχύει
ισχύει  .
.Έτσι η (1) γίνεται
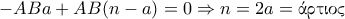 .
.Έτσι, το ζητούμενο ισχύει (δηλαδή να μην γίνεται το άθροισμα των αποστάσεων να είναι το ίδιο) όταν
 .
.Η αρχική περίπτωση για
 γίνεται προφανής αφού
γίνεται προφανής αφού  περιττός.
περιττός.

 τα σημεία με
τα σημεία με ![a_{i}\notin [0,1],i=1,2,...n a_{i}\notin [0,1],i=1,2,...n](/forum/ext/geomar/texintegr/latexrender/pictures/f2a53a40b94140c228c6db8405dbb11d.png)




![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) πρέπει να είναι σταθερή.
πρέπει να είναι σταθερή. .
.
 διασταυρώσεις αν πάρουμε τον πιο σύντομο/σβέλτο δρόμο. Άλλη κατεύθυνση δίνει
διασταυρώσεις αν πάρουμε τον πιο σύντομο/σβέλτο δρόμο. Άλλη κατεύθυνση δίνει 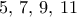 διασταυρώσεις, πάντως περιττό πλήθος.
διασταυρώσεις, πάντως περιττό πλήθος.  με το
με το  ;
; } , όπου
} , όπου  .
.
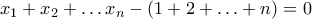 (αφού οι
(αφού οι  είναι αναδιάταξη των
είναι αναδιάταξη των  ).
).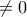 , άτοπο.
, άτοπο.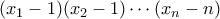 είναι άρτιος.
είναι άρτιος. το σύνολο των ζευγών αριθμών του πίνακα
το σύνολο των ζευγών αριθμών του πίνακα  ,με
,με  , τα οποία δεν είναι διατεταγμένα κατά αύξουσα σειρά στον πίνακα, δηλαδή για τα οποία το
, τα οποία δεν είναι διατεταγμένα κατά αύξουσα σειρά στον πίνακα, δηλαδή για τα οποία το  είναι τοποθετημένο πιο μετά από το
είναι τοποθετημένο πιο μετά από το  .
. )
) όπως ζητείται.
όπως ζητείται. και
και  αντίστοιχα, άρα το άθροισμα τους είναι άρτιο, δηλαδή
αντίστοιχα, άρα το άθροισμα τους είναι άρτιο, δηλαδή  .
.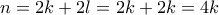 .
. θα κινείται για ακέραιο αριθμό ωρών.
θα κινείται για ακέραιο αριθμό ωρών.