Δίνεται αριθμός με
 μηδενικά που είναι γραμμένος ως
μηδενικά που είναι γραμμένος ως  , στον οποίο το
, στον οποίο το  και το
και το  εναλλάσσονται. Αποδείξτε ότι αυτός ο αριθμός δεν είναι πρώτος.
εναλλάσσονται. Αποδείξτε ότι αυτός ο αριθμός δεν είναι πρώτος.Συντονιστές: achilleas, emouroukos, silouan
 μηδενικά που είναι γραμμένος ως
μηδενικά που είναι γραμμένος ως  , στον οποίο το
, στον οποίο το  και το
και το  εναλλάσσονται. Αποδείξτε ότι αυτός ο αριθμός δεν είναι πρώτος.
εναλλάσσονται. Αποδείξτε ότι αυτός ο αριθμός δεν είναι πρώτος..Κατερινόπουλος Νικόλας έγραψε: ↑Παρ Ιαν 12, 2018 4:32 pmΔίνεται αριθμός μεμηδενικά που είναι γραμμένος ως
, στον οποίο το
και το
εναλλάσσονται. Αποδείξτε ότι αυτός ο αριθμός δεν είναι πρώτος.
 ψηφίων, γράφεται ως
ψηφίων, γράφεται ως  .
.  . Θα δούμε ότι και τα δύο κλάσματα είναι, τελικά, ακέραιοι, οπότε ο αριθμός είναι σύνθετος. Προχωράμε με δύο τρόπους, ο καθένας με τα πλεονεκτήματά του:
. Θα δούμε ότι και τα δύο κλάσματα είναι, τελικά, ακέραιοι, οπότε ο αριθμός είναι σύνθετος. Προχωράμε με δύο τρόπους, ο καθένας με τα πλεονεκτήματά του: . Το δεύτερο είναι επίσης ακέραιος από το κριτήριο διαιρετότητας του
. Το δεύτερο είναι επίσης ακέραιος από το κριτήριο διαιρετότητας του  (έχει έναν άσσο σε άρτια θέση και έναν σε περιττή).
(έχει έναν άσσο σε άρτια θέση και έναν σε περιττή). και
και  , πάντως ακέραιοι
, πάντως ακέραιοι  και οι δύο.
και οι δύο. ψηφία στην θέση των
ψηφία στην θέση των 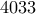 του δοθέντος.
του δοθέντος. είναι σύνθετοι, εκτός του
είναι σύνθετοι, εκτός του  . Για αριθμούς με
. Για αριθμούς με  ψηφία, ουσιαστικά το είδαμε στο προηγούμενο ποστ. Για αριθμούς με
ψηφία, ουσιαστικά το είδαμε στο προηγούμενο ποστ. Για αριθμούς με  θα δείξουμε ότι είναι όλοι πολλαπάσια του
θα δείξουμε ότι είναι όλοι πολλαπάσια του  .
. 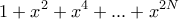 παραγοντοποιούνται ως γινόμενο δύο ακέραιων πολυωνύμων βαθμού
παραγοντοποιούνται ως γινόμενο δύο ακέραιων πολυωνύμων βαθμού 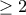 . Για
. Για  έχουμε τα παραπάνω.
έχουμε τα παραπάνω.  άρτιος,
άρτιος,  , έχουμε
, έχουμε 

 περιττός,
περιττός,  , έχουμε
, έχουμε 
 , άρα έχει παράγοντα τον
, άρα έχει παράγοντα τον  και λοιπά).
και λοιπά).Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης