Η άσκηση πού έδωσε ο Αποστόλης ΕΔΩ για τη Γ΄ Γυμνασίου μού έδωσε την ιδέα της προέκτασης του θέματος. Ζητώ να αντιμετωπίσουμε την άσκηση με όσο το δυνατόν περισσότερους τρόπους, δίχως περιορισμό "ύλης". Γι' αυτό και τοποθετώ το ερώτημα εδώ. Πιστεύω ότι είναι αρκούντως διασκεδαστικό.
Έχω μερικές διαφορετικές λύσεις, κάποιες κομψές και διδακτικές, κάποιες τραβηγμένες (τριγωνομετρικές), αλλά πάντως αποτελεσματικές. Περιμένω τις δικές σας πρώτα.
Αν για τους αριθμούς
 ισχύει
ισχύει  , δείξτε ότι ένας τουλάχιστον από τους αριθμούς
, δείξτε ότι ένας τουλάχιστον από τους αριθμούς  είναι ίσος με
είναι ίσος με  .
.Μεταφέρω εδώ τις λύσεις του Χαράλαμπου και του Αποστόλη, αλλάζοντας λίγο τη διατύπωση, αλλά όχι την κεντρική ιδέα.
1η λύση:
Η ισότητα της υπόθεσης γράφεται διαδοχικά:

 .
.2η λύση
Έστω ότι για τους αριθμούς
 ισχύει
ισχύει 
Το τριώνυμο
 παραγοντοποιείται ως εξής:
παραγοντοποιείται ως εξής: 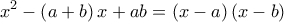 .
.Επειδή, λόγω της (1) ο αριθμός
 είναι ρίζα του
είναι ρίζα του 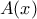 , θα είναι
, θα είναι  , οπότε
, οπότε 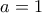 ή
ή 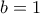 .
.edit: Διόρθωσα ένα τυπογραφικό με την υπόδειξη του Μιχάλη Λάμπρου. Μιχάλη ευχαριστώ!

 . Αν
. Αν  ...τέλος , αλλιώς
...τέλος , αλλιώς 
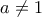 . Από την υπόθεση είναι :
. Από την υπόθεση είναι :  .
. .
. άρα
άρα  .
. παίρνει όλες τις τιμές εκτός από την τιμή
παίρνει όλες τις τιμές εκτός από την τιμή  και
και  τότε μπορώ να βρω
τότε μπορώ να βρω  με
με  και
και  . Τότε όμως έχω:
. Τότε όμως έχω:
 . Επαγωγικά βλέπουμε ότι ισχύει
. Επαγωγικά βλέπουμε ότι ισχύει  . Παίρνοντας όριο
. Παίρνοντας όριο  , και επειδή το όριο του (σταθερού) δεξιού μέλους υπάρχει, θα υπάρχει και του αριστερού. Οπότε είτε
, και επειδή το όριο του (σταθερού) δεξιού μέλους υπάρχει, θα υπάρχει και του αριστερού. Οπότε είτε  (τελειώσαμε) ή
(τελειώσαμε) ή  . Αν
. Αν  . Σε αυτή την περίπτωση στο όριο η
. Σε αυτή την περίπτωση στο όριο η  γίνεται
γίνεται  , που πάλι τελειώσαμε: Να λες ευτυχώς γιατί άλλη μια τέτοια γραμμή και θα πέφτανε πέτρες.
, που πάλι τελειώσαμε: Να λες ευτυχώς γιατί άλλη μια τέτοια γραμμή και θα πέφτανε πέτρες.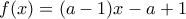
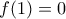 και από την υπόθεση προκύπτει ότι και
και από την υπόθεση προκύπτει ότι και 
 επειδή η
επειδή η  είναι πολυωνυμική α' βαθμού δεν μπορεί να έχει περισσότερες από μία ρίζες, άρα
είναι πολυωνυμική α' βαθμού δεν μπορεί να έχει περισσότερες από μία ρίζες, άρα 
 τότε η
τότε η 
 ).
). δεν έχουμε τίποτα παραπάνω να αποδείξουμε.
δεν έχουμε τίποτα παραπάνω να αποδείξουμε. . Θα αποδείξουμε ότι ισχύει
. Θα αποδείξουμε ότι ισχύει  με
με 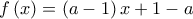 είναι γνησίως αύξουσα αν
είναι γνησίως αύξουσα αν  και γνησίως φθίνουσα αν
και γνησίως φθίνουσα αν  , οπότε και στις δύο περιπτώσεις είναι «1-1».
, οπότε και στις δύο περιπτώσεις είναι «1-1». και
και  , λόγω της (1), οπότε είναι
, λόγω της (1), οπότε είναι  , οπότε :
, οπότε :  . Η σχέση :
. Η σχέση :  , γίνεται
, γίνεται και λύνοντας ( τριώνυμο του
και λύνοντας ( τριώνυμο του  ) ,
) ,  , οπότε
, οπότε 


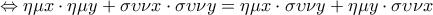

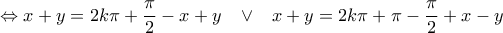
 ,
, , δηλαδή
, δηλαδή  δεν έχουμε να αποδείξουμε τίποτα.Έστω
δεν έχουμε να αποδείξουμε τίποτα.Έστω 

 και
και 


 .
. .
. .
.  κι εμείς έχουμε αποδείξει τη ζητούμενη σχέση.
κι εμείς έχουμε αποδείξει τη ζητούμενη σχέση. , τότε
, τότε  .
. . Θα δείξουμε ότι :
. Θα δείξουμε ότι :  ( οπότε
( οπότε  ,δηλαδή :
,δηλαδή : 
 ό. έ. δ.
ό. έ. δ. , ώστε
, ώστε  .
. .
. .
. , με Θ.Μ.Τ. στο
, με Θ.Μ.Τ. στο ![[1,b] [1,b]](/forum/ext/geomar/texintegr/latexrender/pictures/563e7245b453ee35195e5b0e392b9b72.png) , βρίσκω ότι υπάρχει
, βρίσκω ότι υπάρχει 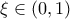 , τέτοιο ώστε :
, τέτοιο ώστε : και επειδή ο αριθμητής ισούται με
και επειδή ο αριθμητής ισούται με  ,
,  , άρα τελικά :
, άρα τελικά :  , τότε
, τότε  . Ομοίως αν
. Ομοίως αν  , τότε
, τότε  .
. απορρίπτεται, αφού το πρώτο μέλος της (1) θα είναι θετικό και το δεύτερο αρνητικό.
απορρίπτεται, αφού το πρώτο μέλος της (1) θα είναι θετικό και το δεύτερο αρνητικό. .
. . Τότε
. Τότε  , άτοπο.
, άτοπο. . Τότε
. Τότε  , άτοπο.
, άτοπο. , τότε
, τότε  . Τότε στο παρακάτω σχήμα το πάνω δεξιά ορθογώνιο θα είχε εμβαδόν
. Τότε στο παρακάτω σχήμα το πάνω δεξιά ορθογώνιο θα είχε εμβαδόν  . Τότε στο παρακάτω σχήμα το πάνω δεξιά ορθογώνιο θα είχε εμβαδόν
. Τότε στο παρακάτω σχήμα το πάνω δεξιά ορθογώνιο θα είχε εμβαδόν  . Τότε στο παρακάτω σχήμα το πάνω δεξιά ορθογώνιο θα είχε εμβαδόν
. Τότε στο παρακάτω σχήμα το πάνω δεξιά ορθογώνιο θα είχε εμβαδόν  και
και  τότε είναι
τότε είναι  .
.  προκύπτει με αντικατάσταση
προκύπτει με αντικατάσταση  .
. δηλ.
δηλ.  δηλ.
δηλ.  τότε
τότε  .
. και
και  , ώστε
, ώστε  (*)
(*)

 ,
,