IMC Stage-II 2017 - mathematica.gr

IMC Stage-II 2017

Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates

Απάντηση

Πρώτη μη αναγνωσμένη δημοσίευση • 48 δημοσιεύσεις

Demetres: Γενικός Συντονιστής; Δημοσιεύσεις: 8989; Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm; Τοποθεσία: Λεμεσός/Πύλα; Επικοινωνία:
Επικοινωνία Demetres

Ιστοσελίδα

IMC Stage-II 2017

Παράθεση

Μη αναγνωσμένη δημοσίευση από Demetres » Δευ Σεπ 18, 2017 11:14 am

Ξεκινάω να βάζω τα θέματα του διαγωνισμού IMC του 2017. Τα περσινά θέματα βρίσκονται εδώ. Θυμίζω ότι απευθύνεται σε μαθητές δημοτικού. Σε κάθε άσκηση ζητείται μόνο η τελική απάντηση χωρίς την οποιαδήποτε δικαιολόγηση. Εδώ όμως ας δούμε πλήρεις εξηγήσεις.

Άσκηση 1: Το άθροισμα των αντιστρόφων τριών θετικών ακεραίων ισούται με

. Είναι γνωστό ότι ένας από αυτούς είναι πολλαπλάσιος του

και ένας άλλος είναι πολλαπλάσιος του

. Το πηλίκο της διαίρεσης του ακεραίου που είναι πολλαπλάσιος του

δια το

, προστίθεται με το πηλίκο της διαίρεσης του ακεραίου που είναι πολλαπλάσιος του

δια το

, δίνοντας άθροισμα

. Ποια είναι η μέγιστη τιμή που μπορεί να πάρει το άθροισμα

;

Άσκηση 2: Ο Weni κόβει κάθετα ένα μεγάλο καρβέλι ψωμί χωρίζοντας το σε

ίσες φέτες. Η Lia και η Anggi κόβουν κάθετα με την ίδια διεύθυνση το ίδιο καρβέλι ψωμί αλλά σε

και

ίσες φέτες αντίστοιχα. Πόσες φέτες ψωμί (όχι αναγκαστικά ίσες) έχουν απομείνει στο τέλος;

Άσκηση 3: Το ορθογώνιο ABCD

έχει εμβαδόν $2016 \mathrm{cm}^2$ . Το

είναι σημείο του

και το

είναι σημείο του

έτσι ώστε το

να είναι παράλληλο του

. Η απόσταση του

από το

είναι διπλάσια από την απόσταση του

από το

. Η απόσταση του

από το

είναι διπλάσια από την απόσταση του

από το

και η απόσταση του

από το

είναι διπλάσια από την απόσταση του

από το

. H απόσταση του

από το

είναι διπλάσια από την απόσταση του

από το

. Η απόσταση του

από το

είναι διπλάσια από την απόσταση του

από το

. Βρείτε το εμβαδόν του τριγώνου XYZ

σε $\mathrm{cm}^2$ .

: Screen Shot 2017-09-22 at 11.44.23.png (14.3 KiB) Προβλήθηκε 2652 φορές

Άσκηση 4: Δύο παίκτες

και

, ξεκινούν με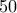

δολάρια ο καθένας παίζοντας μεταξύ τους ένα παιχνίδι τζόγου, ρίχνοντας διαδοχικά ένα νόμισμα. Αν η ένδειξη του νομίσματος είναι κορώνα τότε ο παίκτης που έριξε το νόμισμα παίρνει

δολάρια από τον αντίπαλό του, διαφορετικά (αν η ένδειξη είναι Γράμματα) τότε ο παίκτης που έριξε το νόμισμα δίνει

δολάρια στον αντίπαλό του. Με το τέλος του παιχνιδιού ο κάθε παίκτης έριξε το νόμισμα

φορές και ο

έχει

δολάρια περισσότερα από τον

. Αν ο

στις δέκα φορές που έριξε το νόμισμα εμφανίστηκε κορώνα

φορές, να βρείτε πόσες φορές εμφανίστηκε κορώνα στις δέκα φορές που έριξε το νόμισμα του ο

.

Άσκηση 5: Στο τρίγωνο ABC

, ισχύει ότι $\angle A = 2\angle B$ , ότι η

είναι διχοτόμος της $\angle ACB$ , ότι $AC = 11 \mathrm{cm}$ , και ότι $AD = 2\mathrm{cm}$ . Να βρείτε σε $\mathrm{cm}$ , το μήκος του

.

: Screen Shot 2017-10-02 at 17.39.10.png (21.28 KiB) Προβλήθηκε 2400 φορές

Άσκηση 6: Ο Burton υπολογίζει το ελάχιστο κοινό πολλαπλάσιο μερικών διαδοχικών θετικών ακεραίων που ξεκινούν από το

. Ο Vargas εκτελεί τον ίδιο υπολογισμό, αλλά περιλαμβάνει και τους επόμενους τέσσερις διαδοχικούς θετικούς ακέραιους από τους διαδοχικούς ακέραιους του Burton. Αν και οι δύο βρήκαν την ίδια απάντηση, ποια είναι η μικρότερη δυνατή τιμή του μεγαλύτερου αριθμού των θετικών ακεραίων του Burton;

Άσκηση 7: Το πιο κάτω σχήμα αποτελείται από

ισοσκελή και ορθογώνια τρίγωνα τα οποία είναι τοποθετημένα γύρω από ένα σημείο με τέτοιο τρόπο ώστε η υποτείνουσα του ενός τριγώνου να συμπίπτει με μια κάθετη πλευρά του επόμενου τριγώνου. Αν το συνολικό εμβαδόν και των

τριγώνων είναι $637.5 \mathrm{cm}^2$ , να βρείτε το εμβαδόν του σκιασμένου τριγώνου, σε $\mathrm{cm}^2$ .

: Screen Shot 2017-10-04 at 10.49.40.png (16.1 KiB) Προβλήθηκε 2365 φορές

Άσκηση 8: Η Mary κάθε μέρα γράφει στο τετράδιο της και ένα αριθμό ως εξής: Την πρώτη γράφει τον αριθμό 2017

, και κάθε επόμενη μέρα γράφει το άθροισμα των κύβων των ψηφίων του αριθμού της προηγούμενης μέρας. Ποιο αριθμό έχει γράψει η Μary στο τετράδιο την 2017η μέρα;

Άσκηση 9: Πόσοι τετραψήφιοι αριθμοί υπάρχουν, τέτοιοι ώστε το άθροισμα των τριών πρώτων ψηφίων τους να είναι

, και το άθροισμα των τριών τελευταίων ψηφίων τους να είναι

;

Άσκηση 10: Με πόσους τρόπους μπορούμε να τοποθετήσουμε τα ψηφία 1, 2, 3, 4, 5

και

σε μια ευθεία γραμμή, έτσι ώστε κανένα ζεύγος δύο διπλανών ψηφίων να μην έχει διαφορά ίση με

;

Άσκηση 11: Στο πιο κάτω σχήμα δίνεται ένας πίνακας $4 \times 5$ χωρισμένος σε

ίσα τετραγωνάκια. Το μεσαίο τετραγωνάκι της πρώτης γραμμής του πίνακα είναι σκιασμένο. Πόσα ορθογώνια σχηματίζονται με μερικά από τα

τετραγωνάκια και περιέχουν το σκιασμένο τετραγωνάκι;

$\begin{tikzpicture}[line cap=round,line join=round,>=triangle 45,x=1.0cm,y=1.0cm] \clip(-0.6,-0.6) rectangle (5.6,4.46); \fill[line width=0.8pt,fill=black!20,fill opacity=0.10000000149011612] (2.,4.) -- (2.,3.) -- (3.,3.) -- (3.,4.) -- cycle; \draw [line width=0.8pt] (0.,0.)-- (0.,4.); \draw [line width=0.8pt] (0.,4.)-- (5.,4.); \draw [line width=0.8pt] (5.,4.)-- (5.,0.); \draw [line width=0.8pt] (5.,0.)-- (0.,0.); \draw [line width=0.8pt] (0.,1.)-- (5.,1.); \draw [line width=0.8pt] (0.,2.)-- (5.,2.); \draw [line width=0.8pt] (0.,3.)-- (5.,3.); \draw [line width=0.8pt] (1.,4.)-- (1.,0.); \draw [line width=0.8pt] (2.,0.)-- (2.,4.); \draw [line width=0.8pt] (3.,4.)-- (3.,0.); \draw [line width=0.8pt] (4.,0.)-- (4.,4.); \draw [line width=0.8pt] (2.,4.)-- (2.,3.); \draw [line width=0.8pt] (2.,3.)-- (3.,3.); \draw [line width=0.8pt] (3.,3.)-- (3.,4.); \draw [line width=0.8pt] (3.,4.)-- (2.,4.); \end{tikzpicture}$

Άσκηση 12: Ο Angus έγραψε στον πίνακα όλους τους θετικούς περιττούς αριθμούς από το 1 μέχρι και το 2017. Στην συνέχεια πήρε τον σπόγγο και έσβησε όλα τα άρτια ψηφία των αριθμών. Πόσα ψηφία έμειναν στον πίνακα;

Άσκηση 13: Ένας αριθμός

έχει

ψηφία. Το πρώτο ψηφίο του αριθμού είναι το

. Κάθε δύο γειτονικά ψηφία του αριθμού σχηματίζουν ένα διψήφιο αριθμό ο οποίος διαιρείται με το

ή το

. Υπάρχουν ακριβώς δύο αριθμοί

που σχηματίζονται με τον πιο πάνω τρόπο. Ποια είναι η διαφορά του μεγαλύτερου από τον μικρότερο;

Άσκηση 14: Τα τετράπλευρα ABCD

και $D\,\!EFG$ είναι τετράγωνα, με το

να είναι σημείο της προέκτασης του

όπως φαίνεται στο σχήμα. Το

είναι το μέσο του

και το μήκος του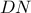

είναι διπλάσιο του

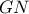. Αν το εμβαδόν του τριγώνου DCE

είναι $14 \mathrm{ cm}^2$ , να βρείτε σε $\mathrm{cm}^2$ , το εμβαδόν του τριγώνου MDN

.

: Screen Shot 2017-10-12 at 14.47.26.png (16.43 KiB) Προβλήθηκε 2250 φορές

Άσκηση 15: Το διάγραμμα στο πιο κάτω σχήμα δείχνει ένα πλέγμα που αποτελείται από

μαύρα τετραγωνάκια και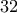

άσπρα τετραγωνάκια. Επιλέγουμε πρώτα ένα μαύρο τετραγωνάκι και στην συνέχεια ένα άσπρο τετραγωνάκι έτσι ώστε τα δύο τετραγωνάκια να μην έχουν κανένα κοινό σημείο. Πόσα διαφορετικά ζεύγη από τετραγωνάκια όπως το πιο πάνω υπάρχουν;

$\begin{tikzpicture}[line cap=round,line join=round,>=triangle 45,x=1.0cm,y=1.0cm,scale=0.8] \clip(-1.18,-0.76) rectangle (8.3,7.52); \fill[line width=2.pt,fill=black,fill opacity=1.0] (0.,7.) -- (0.,6.) -- (1.,6.) -- (1.,7.) -- cycle; \fill[line width=2.pt,fill=black,fill opacity=1.0] (1.,6.) -- (1.,5.) -- (2.,5.) -- (2.,6.) -- cycle; \fill[line width=2.pt,fill=black,fill opacity=1.0] (2.,5.) -- (2.,4.) -- (3.,4.) -- (3.,5.) -- cycle; \fill[line width=2.pt,fill=black,fill opacity=1.0] (3.,4.) -- (3.,3.) -- (4.,3.) -- (4.,4.) -- cycle; \fill[line width=2.pt,fill=black,fill opacity=1.0] (4.,3.) -- (4.,2.) -- (5.,2.) -- (5.,3.) -- cycle; \fill[line width=2.pt,fill=black,fill opacity=1.0] (5.,2.) -- (5.,1.) -- (6.,1.) -- (6.,2.) -- cycle; \fill[line width=2.pt,fill=black,fill opacity=1.0] (6.,1.) -- (6.,0.) -- (7.,0.) -- (7.,1.) -- cycle; \fill[line width=2.pt,fill=black,fill opacity=1.0] (2.,3.) -- (2.,2.) -- (3.,2.) -- (3.,3.) -- cycle; \fill[line width=2.pt,fill=black,fill opacity=1.0] (1.,2.) -- (1.,1.) -- (2.,1.) -- (2.,2.) -- cycle; \fill[line width=2.pt,fill=black,fill opacity=1.0] (0.,1.) -- (0.,0.) -- (1.,0.) -- (1.,1.) -- cycle; \fill[line width=2.pt,fill=black,fill opacity=1.0] (4.,5.) -- (4.,4.) -- (5.,4.) -- (5.,5.) -- cycle; \fill[line width=2.pt,fill=black,fill opacity=1.0] (5.,6.) -- (5.,5.) -- (6.,5.) -- (6.,6.) -- cycle; \fill[line width=2.pt,fill=black,fill opacity=1.0] (6.,7.) -- (6.,6.) -- (7.,6.) -- (7.,7.) -- cycle; \fill[line width=2.pt,fill=black,fill opacity=1.0] (3.,7.) -- (3.,6.) -- (4.,6.) -- (4.,7.) -- cycle; \fill[line width=2.pt,fill=black,fill opacity=1.0] (0.,4.) -- (0.,3.) -- (1.,3.) -- (1.,4.) -- cycle; \fill[line width=2.pt,fill=black,fill opacity=1.0] (6.,4.) -- (6.,3.) -- (7.,3.) -- (7.,4.) -- cycle; \fill[line width=2.pt,fill=black,fill opacity=1.0] (3.,1.) -- (3.,0.) -- (4.,0.) -- (4.,1.) -- cycle; \draw [line width=1.2pt] (0.,7.)-- (0.,0.); \draw [line width=1.2pt] (0.,0.)-- (7.,0.); \draw [line width=1.2pt] (7.,0.)-- (7.,7.); \draw [line width=1.2pt] (7.,7.)-- (0.,7.); \draw [line width=1.2pt] (1.,7.)-- (1.,0.); \draw [line width=1.2pt] (2.,0.)-- (2.,7.); \draw [line width=1.2pt] (3.,7.)-- (3.,0.); \draw [line width=1.2pt] (4.,0.)-- (4.,7.); \draw [line width=1.2pt] (5.,7.)-- (5.,0.); \draw [line width=1.2pt] (6.,0.)-- (6.,7.); \draw [line width=1.2pt] (7.,6.)-- (0.,6.); \draw [line width=1.2pt] (0.,5.)-- (7.,5.); \draw [line width=1.2pt] (7.,4.)-- (0.,4.); \draw [line width=1.2pt] (0.,3.)-- (7.,3.); \draw [line width=1.2pt] (7.,2.)-- (0.,2.); \draw [line width=1.2pt] (0.,1.)-- (7.,1.); \draw [line width=1.2pt] (0.,7.)-- (0.,6.); \draw [line width=1.2pt] (0.,6.)-- (1.,6.); \draw [line width=1.2pt] (1.,6.)-- (1.,7.); \draw [line width=1.2pt] (1.,7.)-- (0.,7.); \draw [line width=1.2pt] (1.,6.)-- (1.,5.); \draw [line width=1.2pt] (1.,5.)-- (2.,5.); \draw [line width=1.2pt] (2.,5.)-- (2.,6.); \draw [line width=1.2pt] (2.,6.)-- (1.,6.); \draw [line width=1.2pt] (2.,5.)-- (2.,4.); \draw [line width=1.2pt] (2.,4.)-- (3.,4.); \draw [line width=1.2pt] (3.,4.)-- (3.,5.); \draw [line width=1.2pt] (3.,5.)-- (2.,5.); \draw [line width=1.2pt] (3.,4.)-- (3.,3.); \draw [line width=1.2pt] (3.,3.)-- (4.,3.); \draw [line width=1.2pt] (4.,3.)-- (4.,4.); \draw [line width=1.2pt] (4.,4.)-- (3.,4.); \draw [line width=1.2pt] (4.,3.)-- (4.,2.); \draw [line width=1.2pt] (4.,2.)-- (5.,2.); \draw [line width=1.2pt] (5.,2.)-- (5.,3.); \draw [line width=1.2pt] (5.,3.)-- (4.,3.); \draw [line width=1.2pt] (5.,2.)-- (5.,1.); \draw [line width=1.2pt] (5.,1.)-- (6.,1.); \draw [line width=1.2pt] (6.,1.)-- (6.,2.); \draw [line width=1.2pt] (6.,2.)-- (5.,2.); \draw [line width=1.2pt] (6.,1.)-- (6.,0.); \draw [line width=1.2pt] (6.,0.)-- (7.,0.); \draw [line width=1.2pt] (7.,0.)-- (7.,1.); \draw [line width=1.2pt] (7.,1.)-- (6.,1.); \draw [line width=1.2pt] (2.,3.)-- (2.,2.); \draw [line width=1.2pt] (2.,2.)-- (3.,2.); \draw [line width=1.2pt] (3.,2.)-- (3.,3.); \draw [line width=1.2pt] (3.,3.)-- (2.,3.); \draw [line width=1.2pt] (1.,2.)-- (1.,1.); \draw [line width=1.2pt] (1.,1.)-- (2.,1.); \draw [line width=1.2pt] (2.,1.)-- (2.,2.); \draw [line width=1.2pt] (2.,2.)-- (1.,2.); \draw [line width=1.2pt] (0.,1.)-- (0.,0.); \draw [line width=1.2pt] (0.,0.)-- (1.,0.); \draw [line width=1.2pt] (1.,0.)-- (1.,1.); \draw [line width=1.2pt] (1.,1.)-- (0.,1.); \draw [line width=1.2pt] (4.,5.)-- (4.,4.); \draw [line width=1.2pt] (4.,4.)-- (5.,4.); \draw [line width=1.2pt] (5.,4.)-- (5.,5.); \draw [line width=1.2pt] (5.,5.)-- (4.,5.); \draw [line width=1.2pt] (5.,6.)-- (5.,5.); \draw [line width=1.2pt] (5.,5.)-- (6.,5.); \draw [line width=1.2pt] (6.,5.)-- (6.,6.); \draw [line width=1.2pt] (6.,6.)-- (5.,6.); \draw [line width=1.2pt] (6.,7.)-- (6.,6.); \draw [line width=1.2pt] (6.,6.)-- (7.,6.); \draw [line width=1.2pt] (7.,6.)-- (7.,7.); \draw [line width=1.2pt] (7.,7.)-- (6.,7.); \draw [line width=1.2pt] (3.,7.)-- (3.,6.); \draw [line width=1.2pt] (3.,6.)-- (4.,6.); \draw [line width=1.2pt] (4.,6.)-- (4.,7.); \draw [line width=1.2pt] (4.,7.)-- (3.,7.); \draw [line width=1.2pt] (0.,4.)-- (0.,3.); \draw [line width=1.2pt] (0.,3.)-- (1.,3.); \draw [line width=1.2pt] (1.,3.)-- (1.,4.); \draw [line width=1.2pt] (1.,4.)-- (0.,4.); \draw [line width=1.2pt] (6.,4.)-- (6.,3.); \draw [line width=1.2pt] (6.,3.)-- (7.,3.); \draw [line width=1.2pt] (7.,3.)-- (7.,4.); \draw [line width=1.2pt] (7.,4.)-- (6.,4.); \draw [line width=1.2pt] (3.,1.)-- (3.,0.); \draw [line width=1.2pt] (3.,0.)-- (4.,0.); \draw [line width=1.2pt] (4.,0.)-- (4.,1.); \draw [line width=1.2pt] (4.,1.)-- (3.,1.); \end{tikzpicture}$

Λέξεις Κλειδιά:

Κατερινόπουλος Νικόλας: Δημοσιεύσεις: 659; Εγγραφή: Κυρ Μαρ 05, 2017 3:24 pm; Τοποθεσία: Καλαμάτα, Μεσσηνία

Re: IMC Stage-II 2017

Παράθεση

Μη αναγνωσμένη δημοσίευση από Κατερινόπουλος Νικόλας » Τρί Σεπ 19, 2017 10:45 pm

Demetres έγραψε: Ξεκινάω να βάζω τα θέματα του διαγωνισμού IMC του 2017. Τα περσινά θέματα βρίσκονται εδώ. Θυμίζω ότι απευθύνεται σε μαθητές δημοτικού. Σε κάθε άσκηση ζητείται μόνο η τελική απάντηση χωρίς την οποιαδήποτε δικαιολόγηση. Εδώ όμως ας δούμε πλήρεις εξηγήσεις.

Άσκηση 1: Το άθροισμα των αντιστρόφων τριών θετικών ακεραίων ισούται με . Είναι γνωστό ότι ένας από αυτούς είναι πολλαπλάσιος του και ένας άλλος είναι πολλαπλάσιος του . Το πηλίκο της διαίρεσης του ακεραίου που είναι πολλαπλάσιος του δια το , προστίθεται με το πηλίκο της διαίρεσης του ακεραίου που είναι πολλαπλάσιος του δια το , δίνοντας άθροισμα . Ποια είναι η μέγιστη τιμή που μπορεί να πάρει το άθροισμα ;

Σύντομα :

$\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=1$ . Έστω ότι 2/x, 3/y

. Άρα ,

Βρίσκουμε απλά τις λύσεις και επιλέγουμε τις κατάλληλες για να επιτευχθεί η μεγαλύτερη τιμή του

.

Το αφήνω μήπως απαντήσει κάποιος άλλος . Αν δεν απαντηθεί , θα βάλω εγώ λύση .

τελευταία επεξεργασία από Κατερινόπουλος Νικόλας σε Τρί Σεπ 19, 2017 10:50 pm, έχει επεξεργασθεί 2 φορές συνολικά.

Κατερινόπουλος Νικόλας: Δημοσιεύσεις: 659; Εγγραφή: Κυρ Μαρ 05, 2017 3:24 pm; Τοποθεσία: Καλαμάτα, Μεσσηνία

Re: IMC Stage-II 2017

Παράθεση

Μη αναγνωσμένη δημοσίευση από Κατερινόπουλος Νικόλας » Τρί Σεπ 19, 2017 10:47 pm

Demetres έγραψε: ↑
Δευ Σεπ 18, 2017 11:14 am

Άσκηση 2: Ο Weni κόβει κάθετα ένα μεγάλο καρβέλι ψωμί χωρίζοντας το σε ίσες φέτες. Η Lia και η Anggi κόβουν κάθετα με την ίδια διεύθυνση το ίδιο καρβέλι ψωμί αλλά σε και ίσες φέτες αντίστοιχα. Πόσες φέτες ψωμί (όχι αναγκαστικά ίσες) έχουν απομείνει στο τέλος;

Η απάντηση είναι 34 αλλά θα φτιάξω σχήμα αύριο . Απλά λέω πως κάποια κοψήματα συμπίπτουν .

Mihalis_Lambrou: Επιμελητής; Δημοσιεύσεις: 15762; Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am

Re: IMC Stage-II 2017

Παράθεση

Μη αναγνωσμένη δημοσίευση από Mihalis_Lambrou » Τετ Σεπ 20, 2017 8:12 pm

Κατερινόπουλος Νικόλας έγραψε: ↑
Τρί Σεπ 19, 2017 10:45 pm
Βρίσκουμε απλά τις λύσεις και επιλέγουμε τις κατάλληλες για να επιτευχθεί η μεγαλύτερη τιμή του .

Ως απάντηση στο πρόβλημα το σχόλιό σου δεν λέει απολύτως τίποτα.

Είναι σαν να ισχυρίζεσαι ότι "για να λύσεις ένα πρόβλημα το μόνο που έχεις να κάνεις είναι να δηλώσεις ότι πρέπει να το λύσεις, και επαναλάβεις την ερώτηση".

Κατερινόπουλος Νικόλας έγραψε: ↑
Τρί Σεπ 19, 2017 10:45 pm
Το αφήνω μήπως απαντήσει κάποιος άλλος . Αν δεν απαντηθεί , θα βάλω εγώ λύση .

Τώρα μάλιστα. Θα χαρούμε να δούμε λύση.

Κατερινόπουλος Νικόλας: Δημοσιεύσεις: 659; Εγγραφή: Κυρ Μαρ 05, 2017 3:24 pm; Τοποθεσία: Καλαμάτα, Μεσσηνία

Re: IMC Stage-II 2017

Παράθεση

Μη αναγνωσμένη δημοσίευση από Κατερινόπουλος Νικόλας » Πέμ Σεπ 21, 2017 4:15 pm

Κύριε Λάμπρου

Σας πληροφορώ ότι δεν έγραψα λύση.

Να η λύση ...

$\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=1$

Χωρίς βλάβη της γενικότητας , παίρνω $2\leq x\leq y \leq z$ .

Άρα , $\dfrac{3}{x}\geq 1$ .

Επομένως x=2, x=3

.

$\cdot$ Αν $\boxed{x=2}$ , $\dfrac{1}{y}+\dfrac{1}{z}=\dfrac{1}{2} \Rightarrow \dfrac{1}{z}=\dfrac{1}{2}-\dfrac{1}{y} \Rightarrow \dfrac{1}{z}=\dfrac{z-2}{2z} \Rightarrow z=\dfrac{2z}{z-2} \Rightarrow z=2+\dfrac{4}{z-2}$ .

Πρέπει z-2/4

. Άρα ,

με τις λύσεις :

(x,y,z)=(2,3,6), (2,4,4), (2,6,3)

. Το τελευταίο απορρίπτεται και το δεύτερο δεν μας κάνει γιατί κανένας δεν είναι

πολλαπλάσιος του

. Άρα , μόνη λύση το $\boxed{(x,y,z)=(2,3,6)}$ , η οποία μας δίνει $\boxed{A=4}$

$\cdot$ Αν $\boxed{x=3}$ , $\dfrac{1}{y}+\dfrac{1}{z}=\dfrac{2}{3} \Rightarrow \dfrac{1}{z}=\dfrac{2}{3}-\dfrac{1}{y} \Rightarrow \dfrac{1}{z}=\dfrac{2y-3}{3y}\Rightarrow$ $z=\dfrac{3y}{2y-3} \Rightarrow z=1,5+\dfrac{4,5}{2y-3}\Rightarrow 2z=3+\dfrac{9}{2y-3}$ .

Πρέπει 2y-3/9

, οπότε

.

Έτσι , παίρνω τις λύσεις :

(x,y,z)=(3,2,6),(3,3,3),(3,6,2)

. Η πρώτη και η τρίτη απορρίπτονται και η δεύτερη δε μας κάνει γιατί

δεν υπάρχει κανείς πολλαπλάσιος του

.

Άρα , η μέγιστη τιμή του

είναι $\boxed{A=4}$ .

Ορέστης Λιγνός: Δημοσιεύσεις: 1835; Εγγραφή: Κυρ Μάιος 08, 2016 7:19 pm; Τοποθεσία: Χαλάνδρι Αττικής; Επικοινωνία:
Επικοινωνία Ορέστης Λιγνός

Ιστοσελίδα

Re: IMC Stage-II 2017

Παράθεση

Μη αναγνωσμένη δημοσίευση από Ορέστης Λιγνός » Πέμ Σεπ 21, 2017 9:10 pm

Η σχέση αυτή είναι λάθος :

Κατερινόπουλος Νικόλας έγραψε: ↑
Πέμ Σεπ 21, 2017 4:15 pm

Χωρίς βλάβη της γενικότητας , παίρνω $2\leq x\leq y \leq z$ .

διότι τα

έχουν συνθήκες ( $2 \mid x, 3 \mid y$ ) .

Πράγματι, για x=6,y=3,z=2

έχουμε

αλλά δεν ισχύει $x \leqslant y \leqslant z$ .

Η απάντηση στο πρόβλημα είναι πράγματι A=4

αλλά ο τρόπος λύσης σου είναι λάθος.

Νικόλα ξανακοίτα το.

Αν δεν απαντηθεί θα βάλω την λύση μου.

Κερδίζουμε ό,τι τολμούμε!

Mihalis_Lambrou: Επιμελητής; Δημοσιεύσεις: 15762; Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am

Re: IMC Stage-II 2017

Παράθεση

Μη αναγνωσμένη δημοσίευση από Mihalis_Lambrou » Παρ Σεπ 22, 2017 1:22 am

Ορέστη, νομίζω ότι είναι απολύτως σωστή η λύση του Νικόλα εκτός αν δεν βλέπω κάτι (ως κουρασμένος από τραχάματα όλη μέρα).

Πράγματι στο μήνυμα #

όπου καταγράφει μόνο υπόδειξη, υπέθεσε 2/x, 3/y

αλλά στην πλήρη λύση που ακολούθησε στο #

έκανε νέα αρχή, χωρίς τον περιορισμό αυτό.

Ουσιαστικά βρήκε όλες τις λύσεις της $\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=1$ με συνθήκη $x\le y \le z$ και μετά επέλεξε τις τριάδες (x,y,z)

έτσι ώστε κάποιος όρος της να είναι το πολλαπλάσιο του

και κάποιος άλλος του

. Ακριβέστερα, από την λύση (2,3,6)

, το πολλαπλάσιο του

είναι ο $6=2\times 3$ και του

είναι ο $3= 3\times 1$ , από όπου A=3+1=4

.

Ορέστης Λιγνός: Δημοσιεύσεις: 1835; Εγγραφή: Κυρ Μάιος 08, 2016 7:19 pm; Τοποθεσία: Χαλάνδρι Αττικής; Επικοινωνία:
Επικοινωνία Ορέστης Λιγνός

Ιστοσελίδα

Re: IMC Stage-II 2017

Παράθεση

Μη αναγνωσμένη δημοσίευση από Ορέστης Λιγνός » Παρ Σεπ 22, 2017 7:32 am

Κύριε Μιχάλη καλημέρα.

Εχεται δίκιο η λύση του Νικόλα είναι σωστή ! Με έφαγε βλέπετε η Γεωγραφία !!

Κάναμε στο μάθημα για την περιστροφή της γης και το Σύμπαν και το μυαλό μου ήταν
σε άλλο Γαλαξία. Ευχαριστώ που με προσγειώσατε !

Να έχετε μια δημιουργική μέρα.

Νικόλα ωραία λύση

Κερδίζουμε ό,τι τολμούμε!

Demetres: Γενικός Συντονιστής; Δημοσιεύσεις: 8989; Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm; Τοποθεσία: Λεμεσός/Πύλα; Επικοινωνία:
Επικοινωνία Demetres

Ιστοσελίδα

Re: IMC Stage-II 2017

Παράθεση

Μη αναγνωσμένη δημοσίευση από Demetres » Παρ Σεπ 22, 2017 11:49 am

Προστέθηκαν οι ασκήσεις 3 και 4. Η απάντηση 34 για την άσκηση 2 είναι σωστή. Ας δούμε όμως και γιατί.

Κατερινόπουλος Νικόλας: Δημοσιεύσεις: 659; Εγγραφή: Κυρ Μαρ 05, 2017 3:24 pm; Τοποθεσία: Καλαμάτα, Μεσσηνία

Re: IMC Stage-II 2017

Παράθεση

Μη αναγνωσμένη δημοσίευση από Κατερινόπουλος Νικόλας » Παρ Σεπ 22, 2017 1:24 pm

Demetres έγραψε: ↑
Δευ Σεπ 18, 2017 11:14 am

Άσκηση 4: Δύο παίκτες και , ξεκινούν με δολάρια ο καθένας παίζοντας μεταξύ τους ένα παιχνίδι τζόγου, ρίχνοντας διαδοχικά ένα νόμισμα. Αν η ένδειξη του νομίσματος είναι κορώνα τότε ο παίκτης που έριξε το νόμισμα παίρνει δολάρια από τον αντίπαλό του, διαφορετικά (αν η ένδειξη είναι Γράμματα) τότε ο παίκτης που έριξε το νόμισμα δίνει δολάρια στον αντίπαλό του. Με το τέλος του παιχνιδιού ο κάθε παίκτης έριξε το νόμισμα φορές και ο έχει δολάρια περισσότερα από τον . Αν ο στις δέκα φορές που έριξε το νόμισμα εμφανίστηκε κορώνα φορές, να βρείτε πόσες φορές εμφανίστηκε κορώνα στις δέκα φορές που έριξε το νόμισμα του ο .

Η απάντηση είναι

.

Ο Α ξεκινάει με 50 δολάρια , όπως και ο Β . Άρα , αφού ο Α ρίχνει 6 φορές κορώνα κερδίζει 24 δολάρια και με 4 φορές που ρίχνει γράμματα χάνει 12 δολάρια . Το κέρδος του συνολικά είναι 12 . Άρα , έχει 62 δολάρια αυτός και 38 ο Β . Για να φτάσει τη διαφορά 42 δολαρίων , ο Α χρειάζεται 18 δολάρια , δηλαδή να ρίξει γράμματα 3 φορές ο Β . Έστω ότι έγινε . Τώρα , ο Β έχει 7 φορές να ρίξει ακόμα . Για να έχει κέρδος μηδέν πρέπει να ισοφαρίσουν οι εφτά φορές με τον εξής τρόπο : Πρέπει να φέρει 3 φορές κορώνα και τέσσερις γράμματα . Άρα συνολικά έριξε κορώνα $\boxed{\text{\gr{3 φορές}}}$

Κατερινόπουλος Νικόλας: Δημοσιεύσεις: 659; Εγγραφή: Κυρ Μαρ 05, 2017 3:24 pm; Τοποθεσία: Καλαμάτα, Μεσσηνία

Re: IMC Stage-II 2017

Παράθεση

Μη αναγνωσμένη δημοσίευση από Κατερινόπουλος Νικόλας » Παρ Σεπ 22, 2017 2:47 pm

Demetres έγραψε: ↑
Παρ Σεπ 22, 2017 11:49 am
Προστέθηκαν οι ασκήσεις 3 και 4. Η απάντηση 34 για την άσκηση 2 είναι σωστή. Ας δούμε όμως και γιατί.

Αν υποθέσουμε ότι δεν συμπίπτουν κοψίματα , οι φέτες είναι 10+15+18=43

. Τα κοψίματα του Weni και της Anggi συμπίπτουν

φορά , στη μέση του ψωμιού . Τα κοψίματα του Weni και της Lia συμπίπτουν

φορές ανά το ένα πέμπτο του ψωμιού και τα κοψίματα της Anggi και της Lia συμπίπτουν

φορές ανά το ένα τρίτο του ψωμιού . Έτσι , έχουμε χάσει 4+2+1=7

φέτες . Συνεπώς υπάρχουν

φέτες .

Δεν ξέρω τι συμβαίνει αλλά τώρα που βάζω την ίδια λύση , μου βγαίνει ΛΑΘΟΣ !!! Μπορεί κάποιος να με βοηθήσει ;

Demetres: Γενικός Συντονιστής; Δημοσιεύσεις: 8989; Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm; Τοποθεσία: Λεμεσός/Πύλα; Επικοινωνία:
Επικοινωνία Demetres

Ιστοσελίδα

Re: IMC Stage-II 2017

Παράθεση

Μη αναγνωσμένη δημοσίευση από Demetres » Παρ Σεπ 22, 2017 3:05 pm

Κατερινόπουλος Νικόλας έγραψε: ↑
Παρ Σεπ 22, 2017 2:47 pm
Αν υποθέσουμε ότι δεν συμπίπτουν κοψίματα , οι φέτες είναι .

Το λάθος είναι εδώ.

Κατερινόπουλος Νικόλας: Δημοσιεύσεις: 659; Εγγραφή: Κυρ Μαρ 05, 2017 3:24 pm; Τοποθεσία: Καλαμάτα, Μεσσηνία

Re: IMC Stage-II 2017

Παράθεση

Μη αναγνωσμένη δημοσίευση από Κατερινόπουλος Νικόλας » Παρ Σεπ 22, 2017 3:07 pm

Demetres έγραψε: ↑
Παρ Σεπ 22, 2017 3:05 pm

Κατερινόπουλος Νικόλας έγραψε: ↑
Παρ Σεπ 22, 2017 2:47 pm
Αν υποθέσουμε ότι δεν συμπίπτουν κοψίματα , οι φέτες είναι .
Το λάθος είναι εδώ.

Ευχαριστώ που με ξυπνήσατε ! Και εκεί συμπίπτουν κάποια κοψίματα άρα οι φέτες είναι λιγότερες από 43 ! Καμιά φορά θέλω διαλυτικό για να ξεκολλήσω !

Filippos Athos: Δημοσιεύσεις: 132; Εγγραφή: Παρ Σεπ 08, 2017 7:45 pm; Τοποθεσία: Λεμεσός

Re: IMC Stage-II 2017

Παράθεση

Μη αναγνωσμένη δημοσίευση από Filippos Athos » Παρ Σεπ 22, 2017 6:22 pm

Demetres έγραψε: ↑
Παρ Σεπ 22, 2017 11:49 am
Προστέθηκαν οι ασκήσεις 3 και 4. Η απάντηση 34 για την άσκηση 2 είναι σωστή. Ας δούμε όμως και γιατί.

Να προσπαθήσω

Ε.Κ.Π. $\displaystyle{(10,15,18)=90$
$90\setminus 10=9$
$90\setminus 15=6&$
$\displaystyle{90\setminus 18=5}$

Κ.Π. $\displaystyle{\left ( 9,6 \right )=\left \{ 18,36,54,72,90 \right \}}$ Άρα έχουμε 5 κομμάτια που συμπίπτουν.
K.Π. $\displaystyle{\left ( 9,5 \right )=\left \{ 45,90 \right \}}$ Άρα έχουμε 2 κομμάτια που συμπίπτουν.
Κ.Π. $\displaystyle{\left ( 6,5 \right )=\left \{ 30,60,90 \right \}}$ Εδώ μετράμε 2 κομμάτια που συμπίπτουν (το 90 δεν το υπολογίζουμε επειδή το έχουμε μετρήσει στις προηγούμενες μετρήσεις)

Άρα σύνολο κομματιών που συμπίπτουν είναι 5+2+2=9

Και τελευταίο $\boxed{43-9=34}$

Mihalis_Lambrou: Επιμελητής; Δημοσιεύσεις: 15762; Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am

Re: IMC Stage-II 2017

Παράθεση

Μη αναγνωσμένη δημοσίευση από Mihalis_Lambrou » Παρ Σεπ 22, 2017 11:07 pm

Demetres έγραψε: ↑
Δευ Σεπ 18, 2017 11:14 am
Άσκηση 1: Το άθροισμα των αντιστρόφων τριών θετικών ακεραίων ισούται με . Είναι γνωστό ότι ένας από αυτούς είναι πολλαπλάσιος του και ένας άλλος είναι πολλαπλάσιος του . Το πηλίκο της διαίρεσης του ακεραίου που είναι πολλαπλάσιος του δια το , προστίθεται με το πηλίκο της διαίρεσης του ακεραίου που είναι πολλαπλάσιος του δια το , δίνοντας άθροισμα . Ποια είναι η μέγιστη τιμή που μπορεί να πάρει το άθροισμα ;

Ας δούμε και μία λύση χωρίς να υπολογίσουμε όλες τις τριάδες που ικανοποιούν την εξίσωση.

Θέλουμε το μέγιστο του a+b

αν $\frac {1}{2a} + \frac {1}{3b}+ \frac {1}{c}=1$ , το οποίο θα δούμε ότι ισούται με

. Πρώτα από όλα είναι $c\ge 2$ (αφού προφανώς $c\ne 1$ ).

Για a=3, b=1, c=2

έχουμε $\frac {1}{2a} + \frac {1}{3b}+ \frac {1}{c}=\frac {1}{6} + \frac {1}{3}+ \frac {1}{2}=1$ οπότε το μέγιστο a+b

είναι τουλάχιστον

. Για την ανάποδη ανισότητα, έχουμε

$1=\frac {1}{2a} + \frac {1}{3b}+ \frac {1}{c} \le \frac {1}{2a} + \frac {1}{3}+ \frac {1}{2}$ άρα $a\le 3$ .

Αν a=1

τότε $1=\frac {1}{2} + \frac {1}{3b}+ \frac {1}{c} > \frac {1}{2} + \frac {1}{c}$ από όπου c>2

δηλαδή $c\ge 3$ . Άρα $1\le \frac {1}{2} + \frac {1}{3b}+ \frac {1}{3}$ , οπότε $b \le 2$ . Σε αυτή την περίπτωση $a+b \le 3< 4$ .

Αν $2 \le a\le 3$ τότε $1=\frac {1}{2a} + \frac {1}{3b}+ \frac {1}{c} \le \frac {1}{4} + \frac {1}{3b}+ \frac {1}{2}$ άρα $b \le \frac {4}{3}$ , οπότε b=1

. Σε αυτή την περίπτωση $a+b\le 3+1=4$ , όπως θέλαμε.

Κατερινόπουλος Νικόλας: Δημοσιεύσεις: 659; Εγγραφή: Κυρ Μαρ 05, 2017 3:24 pm; Τοποθεσία: Καλαμάτα, Μεσσηνία

Re: IMC Stage-II 2017

Παράθεση

Μη αναγνωσμένη δημοσίευση από Κατερινόπουλος Νικόλας » Κυρ Σεπ 24, 2017 11:12 am

Filippos Athos έγραψε: ↑
Παρ Σεπ 22, 2017 6:22 pm

Να προσπαθήσω
Ε.Κ.Π. $\displaystyle{(10,15,18)=90$
$90\setminus 10=9$
$90\setminus 15=6&$
$\displaystyle{90\setminus 18=5}$

Κ.Π. $\displaystyle{\left ( 9,6 \right )=\left \{ 18,36,54,72,90 \right \}}$ Άρα έχουμε 5 κομμάτια που συμπίπτουν.
K.Π. $\displaystyle{\left ( 9,5 \right )=\left \{ 45,90 \right \}}$ Άρα έχουμε 2 κομμάτια που συμπίπτουν.
Κ.Π. $\displaystyle{\left ( 6,5 \right )=\left \{ 30,60,90 \right \}}$ Εδώ μετράμε 2 κομμάτια που συμπίπτουν (το 90 δεν το υπολογίζουμε επειδή το έχουμε μετρήσει στις προηγούμενες μετρήσεις)

Άρα σύνολο κομματιών που συμπίπτουν είναι
Και τελευταίο $\boxed{43-9=34}$

Φίλιππε ωραία λύση !

Αυτή ήταν η αρχική αλλά μετά δεν ξέρω γιατί σκέφτηκα αυτήν που έβαλα πιο πάνω και δεν μου έβγαινε !

Κατερινόπουλος Νικόλας: Δημοσιεύσεις: 659; Εγγραφή: Κυρ Μαρ 05, 2017 3:24 pm; Τοποθεσία: Καλαμάτα, Μεσσηνία

Re: IMC Stage-II 2017

Παράθεση

Μη αναγνωσμένη δημοσίευση από Κατερινόπουλος Νικόλας » Κυρ Σεπ 24, 2017 5:24 pm

Demetres έγραψε: ↑
Δευ Σεπ 18, 2017 11:14 am
Ξεκινάω να βάζω τα θέματα του διαγωνισμού IMC του 2017. Τα περσινά θέματα βρίσκονται εδώ. Θυμίζω ότι απευθύνεται σε μαθητές δημοτικού. Σε κάθε άσκηση ζητείται μόνο η τελική απάντηση χωρίς την οποιαδήποτε δικαιολόγηση. Εδώ όμως ας δούμε πλήρεις εξηγήσεις.

Άσκηση 1: Το άθροισμα των αντιστρόφων τριών θετικών ακεραίων ισούται με . Είναι γνωστό ότι ένας από αυτούς είναι πολλαπλάσιος του και ένας άλλος είναι πολλαπλάσιος του . Το πηλίκο της διαίρεσης του ακεραίου που είναι πολλαπλάσιος του δια το , προστίθεται με το πηλίκο της διαίρεσης του ακεραίου που είναι πολλαπλάσιος του δια το , δίνοντας άθροισμα . Ποια είναι η μέγιστη τιμή που μπορεί να πάρει το άθροισμα ;

Άσκηση 2: Ο Weni κόβει κάθετα ένα μεγάλο καρβέλι ψωμί χωρίζοντας το σε ίσες φέτες. Η Lia και η Anggi κόβουν κάθετα με την ίδια διεύθυνση το ίδιο καρβέλι ψωμί αλλά σε και ίσες φέτες αντίστοιχα. Πόσες φέτες ψωμί (όχι αναγκαστικά ίσες) έχουν απομείνει στο τέλος;

Άσκηση 3: Το ορθογώνιο έχει εμβαδόν $2016 \mathrm{cm}^2$ . Το είναι σημείο του και το είναι σημείο του έτσι ώστε το να είναι παράλληλο του . Η απόσταση του από το είναι διπλάσια από την απόσταση του από το . Η απόσταση του από το είναι διπλάσια από την απόσταση του από το και η απόσταση του από το είναι διπλάσια από την απόσταση του από το . H απόσταση του από το είναι διπλάσια από την απόσταση του από το . Η απόσταση του από το είναι διπλάσια από την απόσταση του από το . Βρείτε το εμβαδόν του τριγώνου σε $\mathrm{cm}^2$ .

Άσκηση 4: Δύο παίκτες και , ξεκινούν με δολάρια ο καθένας παίζοντας μεταξύ τους ένα παιχνίδι τζόγου, ρίχνοντας διαδοχικά ένα νόμισμα. Αν η ένδειξη του νομίσματος είναι κορώνα τότε ο παίκτης που έριξε το νόμισμα παίρνει δολάρια από τον αντίπαλό του, διαφορετικά (αν η ένδειξη είναι Γράμματα) τότε ο παίκτης που έριξε το νόμισμα δίνει δολάρια στον αντίπαλό του. Με το τέλος του παιχνιδιού ο κάθε παίκτης έριξε το νόμισμα φορές και ο έχει δολάρια περισσότερα από τον . Αν ο στις δέκα φορές που έριξε το νόμισμα εμφανίστηκε κορώνα φορές, να βρείτε πόσες φορές εμφανίστηκε κορώνα στις δέκα φορές που έριξε το νόμισμα του ο .

Καλησπέρα κύριε Δημήτρη !

Μπορείτε να μου δώσετε μια υπόδειξη για το τρία ή να δημοσιεύσετε και τα άλλα δύο θέματα ; Έχω κολλήσει ...

Filippos Athos: Δημοσιεύσεις: 132; Εγγραφή: Παρ Σεπ 08, 2017 7:45 pm; Τοποθεσία: Λεμεσός

Re: IMC Stage-II 2017

Παράθεση

Μη αναγνωσμένη δημοσίευση από Filippos Athos » Κυρ Οκτ 01, 2017 9:47 am

Demetres έγραψε: ↑
Δευ Σεπ 18, 2017 11:14 am
Ξεκινάω να βάζω τα θέματα του διαγωνισμού IMC του 2017. Τα περσινά θέματα βρίσκονται εδώ. Θυμίζω ότι απευθύνεται σε μαθητές δημοτικού. Σε κάθε άσκηση ζητείται μόνο η τελική απάντηση χωρίς την οποιαδήποτε δικαιολόγηση. Εδώ όμως ας δούμε πλήρεις εξηγήσεις.

Άσκηση 1: Το άθροισμα των αντιστρόφων τριών θετικών ακεραίων ισούται με . Είναι γνωστό ότι ένας από αυτούς είναι πολλαπλάσιος του και ένας άλλος είναι πολλαπλάσιος του . Το πηλίκο της διαίρεσης του ακεραίου που είναι πολλαπλάσιος του δια το , προστίθεται με το πηλίκο της διαίρεσης του ακεραίου που είναι πολλαπλάσιος του δια το , δίνοντας άθροισμα . Ποια είναι η μέγιστη τιμή που μπορεί να πάρει το άθροισμα ;

Άσκηση 2: Ο Weni κόβει κάθετα ένα μεγάλο καρβέλι ψωμί χωρίζοντας το σε ίσες φέτες. Η Lia και η Anggi κόβουν κάθετα με την ίδια διεύθυνση το ίδιο καρβέλι ψωμί αλλά σε και ίσες φέτες αντίστοιχα. Πόσες φέτες ψωμί (όχι αναγκαστικά ίσες) έχουν απομείνει στο τέλος;

Άσκηση 3: Το ορθογώνιο έχει εμβαδόν $2016 \mathrm{cm}^2$ . Το είναι σημείο του και το είναι σημείο του έτσι ώστε το να είναι παράλληλο του . Η απόσταση του από το είναι διπλάσια από την απόσταση του από το . Η απόσταση του από το είναι διπλάσια από την απόσταση του από το και η απόσταση του από το είναι διπλάσια από την απόσταση του από το . H απόσταση του από το είναι διπλάσια από την απόσταση του από το . Η απόσταση του από το είναι διπλάσια από την απόσταση του από το . Βρείτε το εμβαδόν του τριγώνου σε $\mathrm{cm}^2$ .

Screen Shot 2017-09-22 at 11.44.23.png

Άσκηση 4: Δύο παίκτες και , ξεκινούν με δολάρια ο καθένας παίζοντας μεταξύ τους ένα παιχνίδι τζόγου, ρίχνοντας διαδοχικά ένα νόμισμα. Αν η ένδειξη του νομίσματος είναι κορώνα τότε ο παίκτης που έριξε το νόμισμα παίρνει δολάρια από τον αντίπαλό του, διαφορετικά (αν η ένδειξη είναι Γράμματα) τότε ο παίκτης που έριξε το νόμισμα δίνει δολάρια στον αντίπαλό του. Με το τέλος του παιχνιδιού ο κάθε παίκτης έριξε το νόμισμα φορές και ο έχει δολάρια περισσότερα από τον . Αν ο στις δέκα φορές που έριξε το νόμισμα εμφανίστηκε κορώνα φορές, να βρείτε πόσες φορές εμφανίστηκε κορώνα στις δέκα φορές που έριξε το νόμισμα του ο .

Καλημέρα, μπορεί κάποιος να με βοηθήσει στο πώς να ξεκινήσω την άσκηση 3;

Demetres: Γενικός Συντονιστής; Δημοσιεύσεις: 8989; Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm; Τοποθεσία: Λεμεσός/Πύλα; Επικοινωνία:
Επικοινωνία Demetres

Ιστοσελίδα

Re: IMC Stage-II 2017

Παράθεση

Μη αναγνωσμένη δημοσίευση από Demetres » Κυρ Οκτ 01, 2017 11:27 am

Filippos Athos έγραψε: ↑
Κυρ Οκτ 01, 2017 9:47 am
Καλημέρα, μπορεί κάποιος να με βοηθήσει στο πώς να ξεκινήσω την άσκηση 3;

Καλημέρα.

Προσπάθησε να συγκρίνεις την βάση

με το

. Ακολούθως προσπάθησε να συγκρίνεις το ύψος του τριγώνου, από το

με το

.

Filippos Athos: Δημοσιεύσεις: 132; Εγγραφή: Παρ Σεπ 08, 2017 7:45 pm; Τοποθεσία: Λεμεσός

Re: IMC Stage-II 2017

Παράθεση

Μη αναγνωσμένη δημοσίευση από Filippos Athos » Δευ Οκτ 02, 2017 4:06 pm

Demetres έγραψε: ↑
Κυρ Οκτ 01, 2017 11:27 am

Filippos Athos έγραψε: ↑
Κυρ Οκτ 01, 2017 9:47 am
Καλημέρα, μπορεί κάποιος να με βοηθήσει στο πώς να ξεκινήσω την άσκηση 3;
Καλημέρα.

Προσπάθησε να συγκρίνεις την βάση με το . Ακολούθως προσπάθησε να συγκρίνεις το ύψος του τριγώνου, από το με το .

Ευχαριστώ κύριε Δημήτρη. Νομίζω έχω βρει σωστή λύση.
$\displaystyle{AB=CD=\alpha}$
$\displaystyle{AD=BC=\beta}$

$\displaystyle{AF=\gamma }$
$\displaystyle{FB=\delta }$

Η βάση του τριγώνου $ZY=\alpha-\frac{1}{3}\gamma -\frac{1}{3}\delta$
$\displaystyle{\gamma +\delta =\alpha$ $\Rightarrow$ } $\gamma =\alpha -\delta$
$ZY=\alpha -\frac{1}{3}\cdot \left ( \alpha -\delta \right )-\frac{1}{3}\cdot \delta$
$ZY=\alpha -\frac{1}{3}\cdot \alpha +\frac{1}{3}\delta -\frac{1}{3}\cdot \delta$
$ZY=\frac{2}{3}\cdot \alpha$
Το ύψος του τρίγωνου από τα στοιχείο που δίνετε ότι η απόσταση του $\displaystyle{X}$ από το $\displaystyle{CD}$ είναι διπλάσια από την απόσταση του $\displaystyle{X}$ από το $\displaystyle{AB}$ βγαίνει $\upsilon =\frac{1}{3}\cdot \beta$

$E\bigtriangleup =\frac{ZY\cdot \upsilon }{2}$

$E\bigtriangleup =\frac{\frac{2}{3}\cdot a\cdot \frac{1}{3}\cdot \beta }{2}$

Γνωρίζουμε ότι $\alpha \cdot \beta =2016\mathrm cm \right \}^2$
$E\bigtriangleup =\frac{\frac{2}{3}\cdot \alpha\cdot \frac{1}{3}\cdot\beta }{2}$
$E\bigtriangleup =\frac{\frac{2}{9}\cdot 2016}{2}$
$E\bigtriangleup =224\mathrm\ cm ^2$

Απάντηση

48 δημοσιεύσεις

Επιστροφή σε “Θέματα διαγωνισμών (ΕΜΕ, ΚΥΜΕ, BMO, JBMO, IMO, Kangaroo κλπ)”

Μέλη σε σύνδεση

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες