Να δείξετε ότι η συνάρτηση
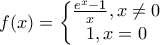 είναι κυρτή στο
είναι κυρτή στο  .
.Ευχαριστώ.
Συντονιστής: KAKABASBASILEIOS
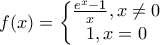 είναι κυρτή στο
είναι κυρτή στο  .
.
 και
και 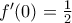

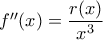
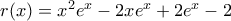
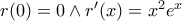

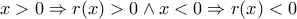
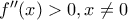
 είναι κυρτή.
είναι κυρτή.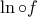 είναι κυρτή στο
είναι κυρτή στο 
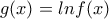


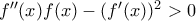
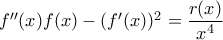
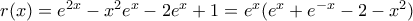

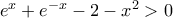 (1)
(1)
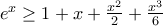 (2)
(2)
 και
και  και προσθέτοντας έχουμε την (1).
και προσθέτοντας έχουμε την (1).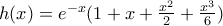
 που δείχνει ότι έχει ολικό μέγιστο στο
που δείχνει ότι έχει ολικό μέγιστο στο 
 προκύπτει άμεσα.
προκύπτει άμεσα.
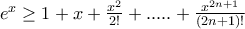

 ενώ το σωστό είναι
ενώ το σωστό είναι  της οποίας
της οποίας ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:Αν
τότε είναι
Αρκεί να δείξουμε ότι για
Αλλά κάνοντας τις πράξεις βρίσκουμε ότι
οπου
Αρκεί για
να είναι(1)
Ειναι για
(2)
με ισότητα αν και μόνο αν
παίρνοντας την (2)γιακαι
και προσθέτοντας έχουμε την (1).
Απόδειξη της (2)
Θεωρούμε την
Είναιπου δείχνει ότι έχει ολικό μέγιστο στο
Αφούπροκύπτει άμεσα.
Με τον ίδιο τρόπο που μπορούμε να δείξουμε ότι για
με ισότητα αν και μόνο αν
Συμπλήρωμα .Διόρθωσα τυπογραφικό.Συγκεκριμένα είχα γράψει ολικό ελάχιστο για τηνενώ το σωστό είναι
ολικό μέγιστο.
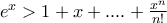 ισχύει και αυτό προκύπτει από το ανάπτυγμα της
ισχύει και αυτό προκύπτει από το ανάπτυγμα της  σε δυναμοσειρά. Έτσι νομίζω ότι φεύγει ένα μελανό σημείο από μια έξυπνη απόδειξη.
σε δυναμοσειρά. Έτσι νομίζω ότι φεύγει ένα μελανό σημείο από μια έξυπνη απόδειξη.Είδατε πουθενά γραμμένο ότι ο μηδενισμός της πρώτης παραγώγου μας δίνει το ακρότατο;Παπαστεργίου Κώστας έγραψε:ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:Αν
τότε είναι
Αρκεί να δείξουμε ότι για
Αλλά κάνοντας τις πράξεις βρίσκουμε ότι
οπου
Αρκεί για
να είναι(1)
Ειναι για
(2)
με ισότητα αν και μόνο αν
παίρνοντας την (2)γιακαι
και προσθέτοντας έχουμε την (1).
Απόδειξη της (2)
Θεωρούμε την
Είναιπου δείχνει ότι έχει ολικό μέγιστο στο
Αφούπροκύπτει άμεσα.
Με τον ίδιο τρόπο που μπορούμε να δείξουμε ότι για
με ισότητα αν και μόνο αν
Συμπλήρωμα .Διόρθωσα τυπογραφικό.Συγκεκριμένα είχα γράψει ολικό ελάχιστο για τηνενώ το σωστό είναι
ολικό μέγιστο.
Ο μηδενισμός της πρώτης παραγώγου σε ένα σημείο δεν αρκεί να το χαρακτηρίσει ως θέση ακροτάτου. Πολύ δε μάλλον ολικό ακρότατο. Δεν είναι γνωστή η μονοτονία της h και δυστυχώς η δευτέρα παράγωγος είναι επίσης 0 και πάει λέγοντας. Έχω να πω όμως ότι η σχέσηισχύει και αυτό προκύπτει από το ανάπτυγμα της
σε δυναμοσειρά. Έτσι νομίζω ότι φεύγει ένα μελανό σημείο από μια έξυπνη απόδειξη.
Πάντως αν θέλαμε να περιοριστούμε σε σχολικά πλαίσια έχω μια απόδειξη την οποία θα ανεβάσω αύριο διότι είναι αργά και είναι λίγο μεγάλη.
Καλόπιστα ΠΚ.
 προκύπτει άμεσα εύκολα η μονοτονία της συνάρτησης και μετά το
προκύπτει άμεσα εύκολα η μονοτονία της συνάρτησης και μετά το 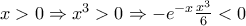
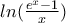 είναι η
είναι η 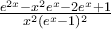 της οποίας το πρόσημο φυσικά καθορίζεται από τον αριθμητή
της οποίας το πρόσημο φυσικά καθορίζεται από τον αριθμητή  με
με 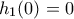 και
και 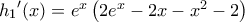 Το πρόσημο αυτής καθορίζεται από το πρόσημο της
Το πρόσημο αυτής καθορίζεται από το πρόσημο της 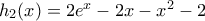 με
με 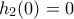 και
και  .Το πρόσημο της
.Το πρόσημο της  καθορίζεται από το πρόσημο της
καθορίζεται από το πρόσημο της  με
με  και
και 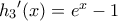 με
με 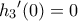 και
και 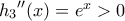
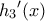 είναι γνησίως αύξουσα άρα
είναι γνησίως αύξουσα άρα  αριστερά του μηδενός και
αριστερά του μηδενός και  δεξιά του. Άρα η
δεξιά του. Άρα η 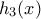 είναι θετική με ελάχιστο το μηδέν. Επομένως η
είναι θετική με ελάχιστο το μηδέν. Επομένως η 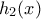 άρα και η
άρα και η 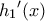
 αριστερά του μηδενός και
αριστερά του μηδενός και  δεξιά του. Έτσι η
δεξιά του. Έτσι η  είναι θετική με ελάχιστο το μηδέν.
είναι θετική με ελάχιστο το μηδέν. 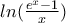 είναι θετική παντού (και στο 0 με πολλαπλά DLH είναι 1/12 αν και δε χρειάζεται). Έτσι η
είναι θετική παντού (και στο 0 με πολλαπλά DLH είναι 1/12 αν και δε χρειάζεται). Έτσι η 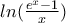 είναι κυρτή.
είναι κυρτή.Μια τέτοια είναι η κυρτήAntonis Loutraris έγραψε:Ένα ακόμη ερώτημα..
Υπάρχει θετική κυρτή συνάρτησητης οποίας
ο λογάριθμος δεν είναι κυρτή συνάρτηση;
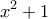 με την
με την 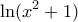 να Μην είναι κυρτή σε όλο το
να Μην είναι κυρτή σε όλο το 
Κύριε Παπαστεργίου, θα ήθελα να δηλώσω απλά (μέσα από τη μικρή μου διαδρομή στοΠαπαστεργίου Κώστας έγραψε:Η νύχτα είναι κακός σύμβουλος και εγώ απρόσεκτος. Ήταν πατάτα. Ίσως είμαι πρόβλημα γιαυτό φεύγω. Να είστε καλά.
Καλημέρα,σας ευχαριστώ για την απάντησή σας. Μετά από καιρό, ήθελα να ρωτήσω, δεν θα έπρεπε και να δείξουμε ότι η παράγωγος τηςΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Παρ Μάιος 12, 2017 4:03 pmΕίναι εύκολο να δείξουμε ότι η
παραγωγίζεται στοκαι
Για
είναι
όπου
Είναι
Από μονοτονία της
έχουμε
Αρα
που δείχνει ότι ηείναι κυρτή.
 είναι συνεχής στο
είναι συνεχής στο  , για να πούμε ότι η
, για να πούμε ότι η  είναι κυρτή σε όλο το
είναι κυρτή σε όλο το  ;
;Εξαρτάται τα Μαθηματικά.Με τα δεδομένα της λύσης είναι άμεσο ότι ηpito έγραψε: ↑Παρ Ιαν 12, 2018 11:29 amΚαλημέρα,σας ευχαριστώ για την απάντησή σας. Μετά από καιρό, ήθελα να ρωτήσω, δεν θα έπρεπε και να δείξουμε ότι η παράγωγος τηςΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Παρ Μάιος 12, 2017 4:03 pmΕίναι εύκολο να δείξουμε ότι η
παραγωγίζεται στοκαι
Για
είναι
όπου
Είναι
Από μονοτονία της
έχουμε
Αρα
που δείχνει ότι ηείναι κυρτή.
είναι συνεχής στο
, για να πούμε ότι η
είναι κυρτή σε όλο το
;
Ευχαριστώ.
 είναι συνεχής.
είναι συνεχής.
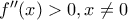
 είναι συνεχής.
είναι συνεχής. είναι γνησίως αύξουσα στα
είναι γνησίως αύξουσα στα 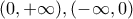

 υπάρχει προκύπτει ότι είναι ίσα με αυτό.
υπάρχει προκύπτει ότι είναι ίσα με αυτό.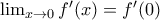
 , είναι σωστό να πούμε ότι η
, είναι σωστό να πούμε ότι η  είναι μη μηδενική στο
είναι μη μηδενική στο  και ως συνεχής διατηρεί σταθερό πρόσημο και αφού
και ως συνεχής διατηρεί σταθερό πρόσημο και αφού  είναι
είναι  για κάθε
για κάθε  στο
στο  παρότι το
παρότι το  είναι το σημείο αλλαγής κλάδου της
είναι το σημείο αλλαγής κλάδου της  ;
;Οι ιδιότητες των συναρτήσεων είναι γενικές και ισχύουν για όλες.

Μέλη σε αυτήν τη Δ. Συζήτηση: Google [Bot] και 24 επισκέπτες