 και
και  το βαρύκεντρό του.
το βαρύκεντρό του. Να βρεθεί σημείο
 στην προέκταση της
στην προέκταση της  ώστε να είναι
ώστε να είναι  , όπου
, όπου  το μέσον της
το μέσον της 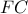 .
.Ευχαριστώ , Γιώργος.
Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 και
και  το βαρύκεντρό του.
το βαρύκεντρό του.  στην προέκταση της
στην προέκταση της  ώστε να είναι
ώστε να είναι  , όπου
, όπου  το μέσον της
το μέσον της 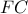 .
.Καλημέρα Γιώργο, Καλημέρα σε όλους!Γιώργος Μήτσιος έγραψε:Καλημέρα σε όλους ! Φρέσκια προσωπική σύνθεση ..
Φρέσκια κατασκευή.PNG
Δίνεται το ισόπλευρο τρίγωνοκαι
το βαρύκεντρό του.
Να βρεθεί σημείοστην προέκταση της
ώστε να είναι
, όπου
το μέσον της
.
Ευχαριστώ , Γιώργος.
 είναι και περίκεντρο, οπότε ο περιγεγραμμένος κύκλος διέρχεται από το
είναι και περίκεντρο, οπότε ο περιγεγραμμένος κύκλος διέρχεται από το  Έστω
Έστω  η πλευρά του ισοπλεύρου και
η πλευρά του ισοπλεύρου και  Είναι:
Είναι:
 και
και 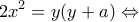
 Από αυτές τις δύο σχέσεις και από νόμο συνημιτόνων στο τρίγωνο
Από αυτές τις δύο σχέσεις και από νόμο συνημιτόνων στο τρίγωνο  με απαλοιφή του
με απαλοιφή του  , καταλήγουμε στην εξίσωση:
, καταλήγουμε στην εξίσωση: ή
ή 
 να πούμε ότι
να πούμε ότι 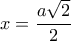 , αλλά ξέρω ότι έχεις ιδιαίτερη αδυναμία στο γράμμα
, αλλά ξέρω ότι έχεις ιδιαίτερη αδυναμία στο γράμμα 
Καλησπέρα στους αγαπητούς Γιώργο και Γιώργο. Καλησπέρα σε όλους .Γιώργος Μήτσιος έγραψε:Καλημέρα σε όλους ! Φρέσκια προσωπική σύνθεση ..
Φρέσκια κατασκευή.PNG
Δίνεται το ισόπλευρο τρίγωνοκαι
το βαρύκεντρό του.
Να βρεθεί σημείοστην προέκταση της
ώστε να είναι
, όπου
το μέσον της
.
Ευχαριστώ , Γιώργος.
 φέρνω παράλληλη στην
φέρνω παράλληλη στην  που τέμνει τον κύκλο του τριγώνου
που τέμνει τον κύκλο του τριγώνου  στο
στο  και μετά η
και μετά η 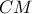
 στο ζητούμενο σημείο
στο ζητούμενο σημείο  .
.  με
με  και
και  οπότε
οπότε 
 τέμνει ακόμα τον κύκλο
τέμνει ακόμα τον κύκλο 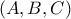 στο
στο  και την
και την  στο
στο  κι έχουμε:
κι έχουμε: κλασσική περίπτωση χρυσής τομής του
κλασσική περίπτωση χρυσής τομής του  .
.Γιώργος Μήτσιος έγραψε:Καλημέρα σε όλους ! Φρέσκια προσωπική σύνθεση ..
Φρέσκια κατασκευή.PNG
Δίνεται το ισόπλευρο τρίγωνοκαι
το βαρύκεντρό του.
Να βρεθεί σημείοστην προέκταση της
ώστε να είναι
, όπου
το μέσον της
.
Ευχαριστώ , Γιώργος.
 η πλευρά του ισόπλευρου τριγώνου
η πλευρά του ισόπλευρου τριγώνου προς την
προς την  περνά από το μέσον
περνά από το μέσον  της
της  και
και 
 και
και  κι ακόμη
κι ακόμη 
 καταλήγουμε στην εξίσωση
καταλήγουμε στην εξίσωση  με δεκτή λύση
με δεκτή λύση 
 στην προέκταση της
στην προέκταση της  ώστε τα
ώστε τα  και
και  να είναι ίσα .Τότε
να είναι ίσα .Τότε 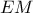 είναι ίσο με την πλευρά του ισοπλεύρου
είναι ίσο με την πλευρά του ισοπλεύρου 
 προς αυτό του τριγώνου
προς αυτό του τριγώνου 
 είναι μικρότερη από
είναι μικρότερη από 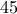 μοίρες .
μοίρες .Γεια σου Γιώργο.Δίνω μια μια απάντηση στα πρόσθετα ερωτήματα.Ίσως υπάρχει ευκολότερηΓιώργος Μήτσιος έγραψε:Kαλημέρα. Να ευχαριστήσω τους αγαπητούς Γιώργο, Νίκο και Μιχάλη για τις εξαιρετικές λύσεις !
Ας δώσω μια επέκταση στο θέμα , θέτοντας νέα -ελπίζω ενδιαφέροντα - ερωτήματα.
Φρέσκια επέκταση.PNG
Στο αρχικό σχήμα , θεωρούμε ακόμη τοστην προέκταση της
ώστε τα
και
να είναι ίσα .Τότε
1) Να δειχθεί ότι τοείναι ίσο με την πλευρά του ισοπλεύρου
2) Να δειχθεί ότι ο λόγος του εμβαδού του τριγώνουπρος αυτό του τριγώνου
είναι .... Ηπειρώτικος δηλαδή ακέραιος !
Αν δεν σας ..παίδεψα αρκετά (ούτε το latex ) τότε βρείτε ένα σχετικά εύκολο τρόπο για να δείξετε ότι
3) Η γωνίαείναι μικρότερη από
μοίρες .
Φιλικά Γιώργος.
 και
και  .Άρα
.Άρα 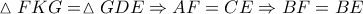
 ισόπλευρο άρα
ισόπλευρο άρα  με
με  μέσον της
μέσον της 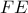
 (Είναι
(Είναι  ).Άρα,
).Άρα,  εγγράψιμο
εγγράψιμο ισοσκελές τραπέζιο άρα εγγράψιμο στον ίδιο κύκλο με το
ισοσκελές τραπέζιο άρα εγγράψιμο στον ίδιο κύκλο με το 
 και
και 
 και
και 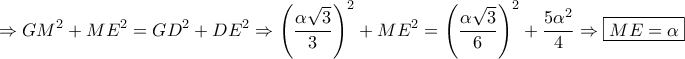

 .Άρα για τις εγγεγραμμένες γωνίες
.Άρα για τις εγγεγραμμένες γωνίες 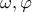 είναι
είναι 
 ,αν ήταν
,αν ήταν  θα είναι
θα είναι  κι έτσι
κι έτσι  που είναι άτοπο .
που είναι άτοπο .
 είναι ισόπλευρο άρα
είναι ισόπλευρο άρα 
 είναι ομοκυκλικά και το τρίγωνο
είναι ομοκυκλικά και το τρίγωνο  του τύπου
του τύπου  .
.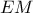 είναι εφαπτόμενο στον περίκυκλο του
είναι εφαπτόμενο στον περίκυκλο του  άρα
άρα 
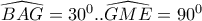 οπότε (βλ. σχήμα)
οπότε (βλ. σχήμα) 
 ενώ
ενώ  ..άρα αρκεί
..άρα αρκεί  .
.  συνεπώς αρκεί
συνεπώς αρκεί  ..δηλ. στο ισοσκελές
..δηλ. στο ισοσκελές  αρκεί
αρκεί 
 ):
): 
 που ισχύει.
που ισχύει.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 12 επισκέπτες