Αν
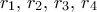 οι ρίζες της
οι ρίζες της  , να βρεθεί η τιμή της παράστασης
, να βρεθεί η τιμή της παράστασης 
Σχόλιο: Υπάρχει λύση με πολλές πράξεις. Η ιδέα είναι να την αποφύγουμε. Πάντως, πέρα από την επίπονη λύση, υπάρχει μία με λίγες γραμμές και υπάρχει μία ακόμα καλύτερη, με δύο γραμμές.
Συντονιστές: achilleas, emouroukos, silouan
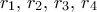 οι ρίζες της
οι ρίζες της  , να βρεθεί η τιμή της παράστασης
, να βρεθεί η τιμή της παράστασης 











ΈχουμεMihalis_Lambrou έγραψε:ΑΣΚΗΣΗ 8
Ανοι ρίζες της
, να βρεθεί η τιμή της παράστασης

 . Παρατηρούμε ότι
. Παρατηρούμε ότι  και κυκλικά. Άρα η δοθείσα ισούται με
και κυκλικά. Άρα η δοθείσα ισούται με 
 .
.Αυτές οι ασκήσεις κλασικής άλγεβρας μου αρέσουν πολύ!Mihalis_Lambrou έγραψε:ΑΣΚΗΣΗ 9
Ανοι ρίζες της
, να δείξετε ότι
 εννοούμε
εννοούμε  και όταν οι δείκτες είναι περισσότεροι από δύο εννοούμε ότι είναι διαφορετικοί μεταξύ τους ανά δύο.
και όταν οι δείκτες είναι περισσότεροι από δύο εννοούμε ότι είναι διαφορετικοί μεταξύ τους ανά δύο.


 δεν είναι λύση της εξίσωσης, άρα
δεν είναι λύση της εξίσωσης, άρα 
 που ικανοποιεί την αρχική εξίσωση ισχύει
που ικανοποιεί την αρχική εξίσωση ισχύει  κι έτσι
κι έτσι 
 .
.




 (εδώ κλέβω λίγο)
(εδώ κλέβω λίγο)Ναι, τοΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:ΑΣΚΗΣΗ 9
...
Από τις σχέσεις του Vieta προκύπτει ότι(εδώ κλέβω λίγο)
οπότε παίρνουμε το ζητούμενο.
 έχει κάποια δουλειά, γι' αυτό υποθέτω ότι ο Αλέξανδρος πήγε μέσω
έχει κάποια δουλειά, γι' αυτό υποθέτω ότι ο Αλέξανδρος πήγε μέσω  .
. (άθροισμα
(άθροισμα  δυνάμεων των ριζών).
δυνάμεων των ριζών). και
και 

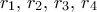 οι ρίζες της
οι ρίζες της  , να δείξετε ότι
, να δείξετε ότι 
 και
και  .
. ,
,  -οστού βαθμού , με
-οστού βαθμού , με  και ακέραιους συντελεστές ,
και ακέραιους συντελεστές , για τέσσερις διαφορετικές μεταξύ τους ακέραιες τιμές του
για τέσσερις διαφορετικές μεταξύ τους ακέραιες τιμές του  , δείξτε
, δείξτε , για καμμιά ακέραια τιμή του
, για καμμιά ακέραια τιμή του  . ( Παλιά σχολική )
. ( Παλιά σχολική )ΟνομάζουμεKARKAR έγραψε:Άσκηση 11
Αν κάποιο πολυώνυμο,
-οστού βαθμού , με
και ακέραιους συντελεστές ,
παίρνει την τιμήγια τέσσερις διαφορετικές μεταξύ τους ακέραιες τιμές του
, δείξτε
ότι το πολυώνυμο δεν παίρνει την τιμή, για καμμιά ακέραια τιμή του
. ( Παλιά σχολική )
 τις τέσσερις διαφορετικές μεταξύ τους ακέραιες τιμές για τις οποίες ισχύει
τις τέσσερις διαφορετικές μεταξύ τους ακέραιες τιμές για τις οποίες ισχύει  και ορίζουμε το πολυώνυμο
και ορίζουμε το πολυώνυμο  .
. με
με  πολυώνυμο με ακέραιους συντελεστές.
πολυώνυμο με ακέραιους συντελεστές. τέτοιος, ώστε
τέτοιος, ώστε  θα είχαμε
θα είχαμε  .
.  θα πρέπει να είναι όλοι διαφορετικοί μεταξύ τους (αφού και οι ακέραιοι
θα πρέπει να είναι όλοι διαφορετικοί μεταξύ τους (αφού και οι ακέραιοι  είναι όλοι διαφορετικοί μεταξύ τους)
είναι όλοι διαφορετικοί μεταξύ τους)  ή
ή  (π.χ.
(π.χ.  ).
).KARKAR έγραψε:Άσκηση 11
( Παλιά σχολική )
Θαυμάσια.nikkru έγραψε: Τότεμε
πολυώνυμο με ακέραιους συντελεστές.
 με ακέραιους συντελεστές γράφεται ως γινόμενο δύο πολυωνύμων
με ακέραιους συντελεστές γράφεται ως γινόμενο δύο πολυωνύμων  με ρητούς συντελεστές τότε γράφεται και ως γινόμενο δύο πολυωνύμων
με ρητούς συντελεστές τότε γράφεται και ως γινόμενο δύο πολυωνύμων  με ακέραιους συντελεστές και με ακριβώς τους ίδιους βαθμούς, αντίστοιχα, με τα
με ακέραιους συντελεστές και με ακριβώς τους ίδιους βαθμούς, αντίστοιχα, με τα  .
. γράφεται ως γινόμενο πολυωνύμων με ρητούς συντελεστές ως
γράφεται ως γινόμενο πολυωνύμων με ρητούς συντελεστές ως  . Όπως εξασφαλίζει το Θεώρημα Gauss, έχουμε και την γραφή
. Όπως εξασφαλίζει το Θεώρημα Gauss, έχουμε και την γραφή  που οι συντελεστές είναι ακέραιοι και οι βαθμοί διατηρούνται.
που οι συντελεστές είναι ακέραιοι και οι βαθμοί διατηρούνται.Γεια σου ΘανάσηKARKAR έγραψε:Η άσκηση είναι από το βιβλίο Β' ΛΥΚΕΙΟΥ Ύλη επιλογής , έκδοση 1981 . Τόσο σ' αυτό , όσο και
στο παραπλήσιας ύλης βιβλίο - σταθμό του Η. Ντζιώρα : Ε' ΓΥΜΝΑΣΙΟΥ , έκδοση 1972 , δεν υπάρχει
αναφορά στο παραπάνω θεώρημα . Νομίζω πάντως , ότι η η υπόδειξη για τη λύση - που είναι
αυτή ακριβώς του nikkru - υπονοεί τη χρήση του . Οπότε , Μιχάλη , θα ήταν επιθυμητό να
αναρτήσεις κάποια απόδειξη ( έστω παραπομπή ) ...
 ενα πολυώνυμο.
ενα πολυώνυμο.


 πολυώνυμο του οποίου οι συντελεστές είναι ακέραιες παραστάσεις
πολυώνυμο του οποίου οι συντελεστές είναι ακέραιες παραστάσεις  και του
και του 
 εχει ακέραιους συντελεστές και το
εχει ακέραιους συντελεστές και το  είναι ακέραιος τότε και
είναι ακέραιος τότε και  είναι ακέραιοι.
είναι ακέραιοι.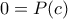 τότε
τότε 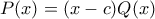 .
. εχει και άλλη ρίζα δηλαδή
εχει και άλλη ρίζα δηλαδή 
 και επαναλαμβάνουμε την διαδικασία.
και επαναλαμβάνουμε την διαδικασία. ισχύει σε κάθε μεταθετικό δακτύλιο.
ισχύει σε κάθε μεταθετικό δακτύλιο.Θανάση, ευχαριστώ θερμά.KARKAR έγραψε:Η άσκηση είναι από το βιβλίο Β' ΛΥΚΕΙΟΥ Ύλη επιλογής , έκδοση 1981 . Τόσο σ' αυτό , όσο και
στο παραπλήσιας ύλης βιβλίο - σταθμό του Η. Ντζιώρα : Ε' ΓΥΜΝΑΣΙΟΥ , έκδοση 1972 , δεν υπάρχει
αναφορά στο παραπάνω θεώρημα .
 τότε δεν χρειαζόμαστε την πλήρη μορφή του θεωρήματος που ανέφερα. Όπως έδειξε ο Σταύρος, εύκολα βλέπουμε ότι "πολυώνυμο με ακέραιους συντελεστές ίσον
τότε δεν χρειαζόμαστε την πλήρη μορφή του θεωρήματος που ανέφερα. Όπως έδειξε ο Σταύρος, εύκολα βλέπουμε ότι "πολυώνυμο με ακέραιους συντελεστές ίσον  επί πολυώνυμο με ακέραιους συντελεστές". Εδώ
επί πολυώνυμο με ακέραιους συντελεστές". Εδώ  ακέραια ρίζα.
ακέραια ρίζα.Παραπάνω είχα αναφερθεί σε δύο αποδείξεις του θεωρήματοςKARKAR έγραψε: θα ήταν επιθυμητό να αναρτήσεις κάποια απόδειξη
 επί πολυώνυμο με ακέραιους συντελεστές, όπου
επί πολυώνυμο με ακέραιους συντελεστές, όπου  ακέραια ρίζα του αρχικού".
ακέραια ρίζα του αρχικού".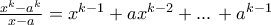 έχει μόνο ακέραιους συντελεστές.
έχει μόνο ακέραιους συντελεστές.
 είναι ακέραιοι και θέλουμε να δείξουμε το ίδιο για τα
είναι ακέραιοι και θέλουμε να δείξουμε το ίδιο για τα 
 στα δύο μέλη έχουμε διαδοχικά
στα δύο μέλη έχουμε διαδοχικά 



 είναι ακέραιος. Με χρήση αυτού στην δεύτερη βγάζουμε ότι ο
είναι ακέραιος. Με χρήση αυτού στην δεύτερη βγάζουμε ότι ο  είναι ακέραιος. Συνεχίζουμε με όμοιο τρόπο προς τα κάτω μέχρι τον τελευταίο, που δείχνει όλοι οι
είναι ακέραιος. Συνεχίζουμε με όμοιο τρόπο προς τα κάτω μέχρι τον τελευταίο, που δείχνει όλοι οι  είναι ακέραιοι, όπως θέλαμε.
είναι ακέραιοι, όπως θέλαμε.α) ΟνομάζωMihalis_Lambrou έγραψε:ΑΣΚΗΣΗ 2
Έστω ότι ηέχει μη μηδενικές ρίζες
.
Βρείτε την τριτοβάθμια εξίσωση που έχει ρίζες τις.
Με χρήση των αποτελεσμάτων σας δείξτε ότι η ικανή και αναγκαία συνθήκη η αρχική εξίσωση να έχει μία ρίζα ίση με το γινόμενο των άλλων δύο είναι
.
Σχόλιο: Η παραπάνω άσκηση μαζί και η προηγούμενη μας δίνει μία τεχνική να βρίσκουμε ικανές και αναγκαίες συνθήκες ώστε τα ισχύει κάποια ταυτότητα μεταξύ των ριζών. Ανάλογα με την περίπτωση, κατασκευάζουμε μία εξίσωση με κατάλληλες ρίζες.
 τις ρίζες της ζητούμενης εξίσωσης.
τις ρίζες της ζητούμενης εξίσωσης. ,
,  και
και .
. ή ισοδύναμα η εξίσωση
ή ισοδύναμα η εξίσωση  (1) έχει ρίζες τις
(1) έχει ρίζες τις  .
. δηλαδή η (1) έχει ρίζα το 1,
δηλαδή η (1) έχει ρίζα το 1,  .
. .
.Νίκο, ευχαριστούμε.Mihalis_Lambrou έγραψε:ΑΣΚΗΣΗ 2
Έστω ότι ηέχει μη μηδενικές ρίζες
.
Βρείτε την τριτοβάθμια εξίσωση που έχει ρίζες τις.
Με χρήση των αποτελεσμάτων σας δείξτε ότι η ικανή και αναγκαία συνθήκη η αρχική εξίσωση να έχει μία ρίζα ίση με το γινόμενο των άλλων δύο είναι
.

 την τυπική ρίζα, ισχύει
την τυπική ρίζα, ισχύει  όπου
όπου  ρίζα της αρχικής. Άρα
ρίζα της αρχικής. Άρα  .
. . Υψώνοντας στο τετράγωνο έχουμε
. Υψώνοντας στο τετράγωνο έχουμε  , άρα
, άρα
 ,
, έχει ρίζες
έχει ρίζες  .
.  .
.
Από τους γενικευμένους τύπους Vieta έχουμεMihalis_Lambrou έγραψε:ΑΣΚΗΣΗ 12
Έστω ότι ηέχει ρίζες
.
Βρείτε την τριτοβάθμια εξίσωση που έχει ρίζες τις.
Σχόλιο: Μπορούμε να αποφύγουμε Vieta, που οδηγεί σε επίπονες πράξεις.
Για έλεγχο δίνω την απάντηση, αλλά παρακαλώ μην την χρησιμοποιήσετε:
Μένει αναπάντηση η ΑΣΚΗΣΗ 10.

 , άρα
, άρα  κι έτσι
κι έτσι 
 και
και  .
. , και
, και  .
. όπου
όπου



 και όμοια
και όμοια 


Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες