ΘΑΛΗΣ 2016
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5561
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
ΘΑΛΗΣ 2016
Τα θέματα του ΘΑΛΗ 2016 !
Χαρείτε τα και στείλτε πλήρεις λύσεις για το αρχείο μας !
Μπ
Χαρείτε τα και στείλτε πλήρεις λύσεις για το αρχείο μας !
Μπ
- Συνημμένα
-
- THEMATA_THALI_12-11-2016F (1).pdf
- (271.65 KiB) Μεταφορτώθηκε 1770 φορές
Λέξεις Κλειδιά:
Re: ΘΑΛΗΣ 2016
Γεωμετρία Γ ΛΥΚΕΙΟΥ .
Επειδή  ,είναι
,είναι  , οπότε το
, οπότε το  είναι το κέντρο του περικύκλου .
είναι το κέντρο του περικύκλου .
Είναι : , συνεπώς τα
, συνεπώς τα  είναι αντιδιαμετρικά .
είναι αντιδιαμετρικά .
 ,είναι
,είναι  , οπότε το
, οπότε το  είναι το κέντρο του περικύκλου .
είναι το κέντρο του περικύκλου .Είναι :
 , συνεπώς τα
, συνεπώς τα  είναι αντιδιαμετρικά .
είναι αντιδιαμετρικά .Re: ΘΑΛΗΣ 2016
ΘΕΜΑ 4- Α ΛΥΚΕΙΟΥΜπάμπης Στεργίου έγραψε:Τα θέματα του ΘΑΛΗ 2016 !
Χαρείτε τα και στείλτε πλήρεις λύσεις για το αρχείο μας !
Μπ
Με
 το γινόμενο
το γινόμενο  ισούται με
ισούται με  .
.Συνεπώς, αν
 έχουμε
έχουμε ,
,δηλ. τέλειο τετράγωνο.
Φιλικά,
ΑχιλλέΑς
Re: ΘΑΛΗΣ 2016
ΘΕΜΑ 1-Β ΛΥΚΕΙΟΥ
Με διαφορά τετραγώνων παίρνουμε
 .
.
Προφανώς , οπότε για να είναι ο
, οπότε για να είναι ο  πρώτος θα πρέπει να είναι
πρώτος θα πρέπει να είναι  , δηλ.
, δηλ. 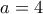 .
.
Με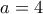 , είναι
, είναι  , που είναι πράγματι πρώτος.
, που είναι πράγματι πρώτος.
Φιλικά,
Αχιλλέας
Με διαφορά τετραγώνων παίρνουμε
 .
.Προφανώς
 , οπότε για να είναι ο
, οπότε για να είναι ο  πρώτος θα πρέπει να είναι
πρώτος θα πρέπει να είναι  , δηλ.
, δηλ. 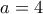 .
.Με
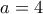 , είναι
, είναι  , που είναι πράγματι πρώτος.
, που είναι πράγματι πρώτος.Φιλικά,
Αχιλλέας
-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: ΘΑΛΗΣ 2016
Θεμα 3-Β ΛΥΚΕΙΟΥ
Για είναι
είναι

οπότε παίρνοντας την τετραγωνική ρίζα έχουμε
 ,
,
Πολλαπλασιάζοντας τις σχέσεις αυτές για παίρνουμε
παίρνουμε

όπως θέλαμε.
Φιλικά,
Αχιλλέας
Για
 είναι
είναι
οπότε παίρνοντας την τετραγωνική ρίζα έχουμε
 ,
,Πολλαπλασιάζοντας τις σχέσεις αυτές για
 παίρνουμε
παίρνουμε
όπως θέλαμε.
Φιλικά,
Αχιλλέας
Re: ΘΑΛΗΣ 2016
Ας το κάνουμε καρτεσιανά : Προφανώς τα  συνευθειακά , δηλαδή
συνευθειακά , δηλαδή  .
.
Οι συντεταγμένες του ( εύκολα με πράξεις ρουτίνας ) , δείχνουν ότι και
( εύκολα με πράξεις ρουτίνας ) , δείχνουν ότι και 
 συνευθειακά , δηλαδή
συνευθειακά , δηλαδή  .
.Οι συντεταγμένες του
 ( εύκολα με πράξεις ρουτίνας ) , δείχνουν ότι και
( εύκολα με πράξεις ρουτίνας ) , δείχνουν ότι και 
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13278
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: ΘΑΛΗΣ 2016
Πρόβλημα 2 - Β Λυκείου
 κι επειδή
κι επειδή  τα σημεία
τα σημεία  είναι συνευθειακά. Είναι επίσης
είναι συνευθειακά. Είναι επίσης 
(κάθετες στην ίδια ευθεία), οπότε το είναι μέσο του
είναι μέσο του  (αφού το
(αφού το  είναι μέσο του
είναι μέσο του  ) και το ζητούμενο έπεται.
) και το ζητούμενο έπεται.
 κι επειδή
κι επειδή  τα σημεία
τα σημεία  είναι συνευθειακά. Είναι επίσης
είναι συνευθειακά. Είναι επίσης 
(κάθετες στην ίδια ευθεία), οπότε το
 είναι μέσο του
είναι μέσο του  (αφού το
(αφού το  είναι μέσο του
είναι μέσο του  ) και το ζητούμενο έπεται.
) και το ζητούμενο έπεται.- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: ΘΑΛΗΣ 2016
Αλλιώς το 4ο της Α Λυκείου:
Αν ορίσουμε τότε
τότε 
Οπότε αν προσθέσουμε στο τον αριθμό
τον αριθμό  τότε
τότε

δηλαδή τέλειο τετράγωνο ακεραίου.
Αλέξανδρος
Αν ορίσουμε
 τότε
τότε 
Οπότε αν προσθέσουμε στο
 τον αριθμό
τον αριθμό  τότε
τότε
δηλαδή τέλειο τετράγωνο ακεραίου.
Αλέξανδρος
Αλέξανδρος Συγκελάκης
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: ΘΑΛΗΣ 2016
4o της Γ Λυκείου
Ο αριθμός είναι της μορφής
είναι της μορφής  ο οποίος γράφεται:
ο οποίος γράφεται:
![x^7+x^2+1=x^7-x+x^2+x+1=x(x^3-1)(x^3+1)+x^2+x+1=x(x-1)(x^2+x+1)(x^3+1)+x^2+x+1=(x^2+x+1)\left[(x(x-1)(x^3+1)+1\right] x^7+x^2+1=x^7-x+x^2+x+1=x(x^3-1)(x^3+1)+x^2+x+1=x(x-1)(x^2+x+1)(x^3+1)+x^2+x+1=(x^2+x+1)\left[(x(x-1)(x^3+1)+1\right]](/forum/ext/geomar/texintegr/latexrender/pictures/5b536f64ec827a748eaea221920c4c53.png)
οπότε ο αριθμός διαιρείται από τον αριθμό
διαιρείται από τον αριθμό  που είναι πράγματι πρώτος αφού δεν διαιρείται από κανένα πρώτο μικρότερο του
που είναι πράγματι πρώτος αφού δεν διαιρείται από κανένα πρώτο μικρότερο του  .
.
Αλέξανδρος
Ο αριθμός
 είναι της μορφής
είναι της μορφής  ο οποίος γράφεται:
ο οποίος γράφεται:![x^7+x^2+1=x^7-x+x^2+x+1=x(x^3-1)(x^3+1)+x^2+x+1=x(x-1)(x^2+x+1)(x^3+1)+x^2+x+1=(x^2+x+1)\left[(x(x-1)(x^3+1)+1\right] x^7+x^2+1=x^7-x+x^2+x+1=x(x^3-1)(x^3+1)+x^2+x+1=x(x-1)(x^2+x+1)(x^3+1)+x^2+x+1=(x^2+x+1)\left[(x(x-1)(x^3+1)+1\right]](/forum/ext/geomar/texintegr/latexrender/pictures/5b536f64ec827a748eaea221920c4c53.png)
οπότε ο αριθμός
 διαιρείται από τον αριθμό
διαιρείται από τον αριθμό  που είναι πράγματι πρώτος αφού δεν διαιρείται από κανένα πρώτο μικρότερο του
που είναι πράγματι πρώτος αφού δεν διαιρείται από κανένα πρώτο μικρότερο του  .
.Αλέξανδρος
Αλέξανδρος Συγκελάκης
Re: ΘΑΛΗΣ 2016
Γεωμετρία Β (αλλιώς)
Προεκτείνοντας τις  , δημιουργείται το παραλληλόγραμμο
, δημιουργείται το παραλληλόγραμμο  και τότε το
και τότε το 
είναι το μέσο της , δηλαδή
, δηλαδή  , αφού το
, αφού το  είναι ορθογώνιο και ισοσκελές .
είναι ορθογώνιο και ισοσκελές .
 , δημιουργείται το παραλληλόγραμμο
, δημιουργείται το παραλληλόγραμμο  και τότε το
και τότε το 
είναι το μέσο της
 , δηλαδή
, δηλαδή  , αφού το
, αφού το  είναι ορθογώνιο και ισοσκελές .
είναι ορθογώνιο και ισοσκελές .Re: ΘΑΛΗΣ 2016
ΘΕΜΑ 4 - Β ΛΥΚΕΙΟΥ
Αφαιρώντας τις δύο πρώτες σχέσεις κατά μέλη παίρνουμε

που γράφεται ισοδύναμα ως
 .
.
Έχουμε τις περιπτώσεις:
(Ι) .
.
Τότε .
.
Aπό τις δύο τελευταίες σχέσεις τις υπόθεσης προκύπτει , κι αφού
, κι αφού  είναι
είναι  .
.
Με η τελευταία σχέση δίνει
η τελευταία σχέση δίνει  και η πρώτη δίνει
και η πρώτη δίνει  .
.
Προσθέτοντας αυτές κατά μέλη κι αφού παίρουμε
παίρουμε
 , δηλ.
, δηλ. 
ή ισοδύναμα με λύσεις
με λύσεις  και
και  .
.
Αφού και
και  αποδεκτή είναι μόνο η
αποδεκτή είναι μόνο η  , οποτε
, οποτε  , και
, και  .
.
Άρα .
.
(ΙI) .
.
Αφαιρώντας τις τελευταίες δύο δοθείσες σχέσεις, αφού θε΄σουμε παίρουμε
παίρουμε

δηλαδή
 ,
,
οπότε .
.
Εύκολα βλέπουμε τότε, προσθέτοντας τις δύο πρώτες σχέσεις ότι , και
, και 
Άρα .
.
Συνοψίζοντας ή
ή  .
.
Φιλικά,
Αχιλλέας
Αφαιρώντας τις δύο πρώτες σχέσεις κατά μέλη παίρνουμε

που γράφεται ισοδύναμα ως
 .
.Έχουμε τις περιπτώσεις:
(Ι)
 .
.Τότε
 .
.Aπό τις δύο τελευταίες σχέσεις τις υπόθεσης προκύπτει
 , κι αφού
, κι αφού  είναι
είναι  .
.Με
 η τελευταία σχέση δίνει
η τελευταία σχέση δίνει  και η πρώτη δίνει
και η πρώτη δίνει  .
. Προσθέτοντας αυτές κατά μέλη κι αφού
 παίρουμε
παίρουμε , δηλ.
, δηλ. 
ή ισοδύναμα
 με λύσεις
με λύσεις  και
και  .
.Αφού
 και
και  αποδεκτή είναι μόνο η
αποδεκτή είναι μόνο η  , οποτε
, οποτε  , και
, και  .
.Άρα
 .
.(ΙI)
 .
.Αφαιρώντας τις τελευταίες δύο δοθείσες σχέσεις, αφού θε΄σουμε
 παίρουμε
παίρουμε
δηλαδή
 ,
,οπότε
 .
.Εύκολα βλέπουμε τότε, προσθέτοντας τις δύο πρώτες σχέσεις ότι
 , και
, και 
Άρα
 .
.Συνοψίζοντας
 ή
ή  .
.Φιλικά,
Αχιλλέας
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: ΘΑΛΗΣ 2016
2ο Α Λυκείου
Επειδή
άρα αφενός ο αριθμός δεν μπορεί να περιέχει τον αριθμό ως ψηφίο (αφού είναι τουλάχιστον
ως ψηφίο (αφού είναι τουλάχιστον  -ψήφιος) και αφετέρου αφού το άθροισμα των ψηφίων είναι
-ψήφιος) και αφετέρου αφού το άθροισμα των ψηφίων είναι  άρα θα είναι είτε
άρα θα είναι είτε  -ψήφιος της μορφής
-ψήφιος της μορφής  (με όλες τις μεταθέσεις των ψηφίων) είτε
(με όλες τις μεταθέσεις των ψηφίων) είτε  -ψήφιος της μορφής
-ψήφιος της μορφής  (με όλες τις μεταθέσεις των ψηφίων).
(με όλες τις μεταθέσεις των ψηφίων).
Αφού ο αριθμός διαιρείται από το άρα το τελευταίο ψηφίο είναι άρτιος, τα δύο τελευταία ψηφία πρέπει να διαιρούνται από το
άρα το τελευταίο ψηφίο είναι άρτιος, τα δύο τελευταία ψηφία πρέπει να διαιρούνται από το  και τα τρία τελευταία ψηφία από το
και τα τρία τελευταία ψηφία από το  .
.
Έτσι από την 1η μορφή κρατάμε μόνο τον αριθμό (Οι επιλογές είναι πολύ λίγες αφού τα
(Οι επιλογές είναι πολύ λίγες αφού τα  τελευταία ψηφία μπορεί να είναι μόνο
τελευταία ψηφία μπορεί να είναι μόνο  ή
ή  ) που διαιρείται από το
) που διαιρείται από το  .
.
Από τη 2η μορφή (τα δύο τελευταία ψηφία είναι αναγκαστικά ο αριθμός για να διαιρείται από το
για να διαιρείται από το  ) και τις
) και τις  δυνατές επιλογές για τα
δυνατές επιλογές για τα  πρώτα ψηφία κρατάμε μόνο τον
πρώτα ψηφία κρατάμε μόνο τον  .
.
Αλέξανδρος
Επειδή

άρα αφενός ο αριθμός δεν μπορεί να περιέχει τον αριθμό
 ως ψηφίο (αφού είναι τουλάχιστον
ως ψηφίο (αφού είναι τουλάχιστον  -ψήφιος) και αφετέρου αφού το άθροισμα των ψηφίων είναι
-ψήφιος) και αφετέρου αφού το άθροισμα των ψηφίων είναι  άρα θα είναι είτε
άρα θα είναι είτε  -ψήφιος της μορφής
-ψήφιος της μορφής  (με όλες τις μεταθέσεις των ψηφίων) είτε
(με όλες τις μεταθέσεις των ψηφίων) είτε  -ψήφιος της μορφής
-ψήφιος της μορφής  (με όλες τις μεταθέσεις των ψηφίων).
(με όλες τις μεταθέσεις των ψηφίων).Αφού ο αριθμός διαιρείται από το
 άρα το τελευταίο ψηφίο είναι άρτιος, τα δύο τελευταία ψηφία πρέπει να διαιρούνται από το
άρα το τελευταίο ψηφίο είναι άρτιος, τα δύο τελευταία ψηφία πρέπει να διαιρούνται από το  και τα τρία τελευταία ψηφία από το
και τα τρία τελευταία ψηφία από το  .
.Έτσι από την 1η μορφή κρατάμε μόνο τον αριθμό
 (Οι επιλογές είναι πολύ λίγες αφού τα
(Οι επιλογές είναι πολύ λίγες αφού τα  τελευταία ψηφία μπορεί να είναι μόνο
τελευταία ψηφία μπορεί να είναι μόνο  ή
ή  ) που διαιρείται από το
) που διαιρείται από το  .
.Από τη 2η μορφή (τα δύο τελευταία ψηφία είναι αναγκαστικά ο αριθμός
 για να διαιρείται από το
για να διαιρείται από το  ) και τις
) και τις  δυνατές επιλογές για τα
δυνατές επιλογές για τα  πρώτα ψηφία κρατάμε μόνο τον
πρώτα ψηφία κρατάμε μόνο τον  .
.Αλέξανδρος
Αλέξανδρος Συγκελάκης
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13278
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: ΘΑΛΗΣ 2016
Γεωμετρία Α Λυκείου
 , άρα τα σημεία
, άρα τα σημεία  είναι συνευθειακά. Έστω
είναι συνευθειακά. Έστω  το σημείο τομής της
το σημείο τομής της  με την
με την  .
.
Θα δείξω ότι τα σημεία είναι συνευθειακά.
είναι συνευθειακά.
Το είναι εγγράψιμο (απέναντι γωνίες παραπληρωματικές), άρα
είναι εγγράψιμο (απέναντι γωνίες παραπληρωματικές), άρα  .
.
Αλλά , οπότε
, οπότε  και το ζητούμενο έπεται.
και το ζητούμενο έπεται.
 , άρα τα σημεία
, άρα τα σημεία  είναι συνευθειακά. Έστω
είναι συνευθειακά. Έστω  το σημείο τομής της
το σημείο τομής της  με την
με την  .
.Θα δείξω ότι τα σημεία
 είναι συνευθειακά.
είναι συνευθειακά.Το
 είναι εγγράψιμο (απέναντι γωνίες παραπληρωματικές), άρα
είναι εγγράψιμο (απέναντι γωνίες παραπληρωματικές), άρα  .
. Αλλά
 , οπότε
, οπότε  και το ζητούμενο έπεται.
και το ζητούμενο έπεται.-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13278
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: ΘΑΛΗΣ 2016
Πρόβλημα 1 - Α Λυκείου
Πολύ απλό.
Η πρώτη ανίσωση:

Η δεύτερη ανίσωση:

Οι ακέραιες κοινές λύσεις είναι
Πολύ απλό.
Η πρώτη ανίσωση:


Η δεύτερη ανίσωση:


Οι ακέραιες κοινές λύσεις είναι

Re: ΘΑΛΗΣ 2016

 Για
Για  είναι
είναι  ,οπότε ένας απο τους
,οπότε ένας απο τους  θα είναι το
θα είναι το  και οι αλλοι
και οι αλλοι ( προφανως στο πλήθος 2)θα είναι ίσοι με το 1.
Οι παραπάνω αριθμοι (1124,1214,2114)δεν ειναι πολλαπλασια του
 και απορριπτονται.
και απορριπτονται. Για
Για  είναι
είναι  ,οπότε
,οπότε  1)ένας θα είναι το 4 και άλλοι ( προφανως στο πλήθος 2) θα είναι ίσοι με το 1.Οι αριθμοί αυτοι είναι :
1)ένας θα είναι το 4 και άλλοι ( προφανως στο πλήθος 2) θα είναι ίσοι με το 1.Οι αριθμοί αυτοι είναι : .απο τους οποίους μόνο ο
.απο τους οποίους μόνο ο  είναι πολλαπλάσιο του
είναι πολλαπλάσιο του 
 2)δύο απο τους
2)δύο απο τους θα είναι ίσοι με το
θα είναι ίσοι με το  και οι άλλοι
και οι άλλοι( προφανως στο πλήθος 2) θα είναι ίσοι με το 1.Οι αριθμοί αυτοί είναι
 ,
,απο τους οποίους μόνο ο
 είναι πολλαπλάσιο του
είναι πολλαπλάσιο του  . Τελικά οι ζητούμενοι αριθμοί είναι
. Τελικά οι ζητούμενοι αριθμοί είναι .
.Ν.Ζ.
Re: ΘΑΛΗΣ 2016
Από την Γ γυμνασίου το 4 β μου φάνηκε λίγο δύσκολο (αλλά το έλυσα). Τι πιστεύετε;
Bye :')
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13278
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: ΘΑΛΗΣ 2016
JimNt. έγραψε:Από την Γ γυμνασίου το 4 β μου φάνηκε λίγο δύσκολο (αλλά το έλυσα). Τι πιστεύετε;
Πράγματι ήταν δυσκολούτσικο. Θα μπορούσε να ήταν κάλλιστα θέμα Ευκλείδη.
Γενικά όμως ήταν ένας πάρα πολύ ωραίος Θαλής αν και λίγο απαιτητικός.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες








