ΈστωKARKAR έγραψε:Άσκηση 211
Στο άκροτης διαγωνίου
, ορθογωνίου
, φέρω κάθετη , η οποία τέμνει τις προεκτάσεις των
στα σημεία
αντίστοιχα . Ονομάζω
το μέσο του
, παίρνω τυχαίο σημείο
της
και γράφω τους κύκλους ,
,
, οι οποίοι τέμνουν τις προεκτάσεις των
στα
αντίστοιχα . Δείξτε ότι οι ευθείες
τέμνονται σε σημείο - το οποίο ονομάζω
- της
.
 , οι περίκυκλοι των τριγώνων
, οι περίκυκλοι των τριγώνων  αντιστοίχως και ας είναι
αντιστοίχως και ας είναι  και
και  .
.Έστω τα σημεία
 και αρκεί να αποδειχθεί ότι
και αρκεί να αποδειχθεί ότι  , γιατί η ευθεία που συνδέει το σημείο τομής των διαγωνίων τραπεζίου με το σημείο τομής των ευθειών των μη παραλλήλων πλευρών του, περνάει από τα μέσα των βάσεών του ( γνωστό αποτέλεσμα ).
, γιατί η ευθεία που συνδέει το σημείο τομής των διαγωνίων τραπεζίου με το σημείο τομής των ευθειών των μη παραλλήλων πλευρών του, περνάει από τα μέσα των βάσεών του ( γνωστό αποτέλεσμα ). Από το εγγράψιμο τετράπλευρο
Από το εγγράψιμο τετράπλευρο  έχουμε
έχουμε 
Από
 και
και  , λόγω του ορθογωνίου τριγώνου
, λόγω του ορθογωνίου τριγώνου 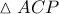 με
με  ,
, προκύπτει

 και ομοίως αποδεικνύεται ότι
και ομοίως αποδεικνύεται ότι 
Από το τραπέζιο
 τώρα, έχουμε
τώρα, έχουμε 
Από το ορθογώνιο παραλληλόγραμμο
 έχουμε
έχουμε 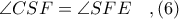
Από

 και άρα, τα σημεία
και άρα, τα σημεία  είναι συνευθειακά.
είναι συνευθειακά.Ομοίως αποδεικνύεται ότι και τα σημεία
 είναι συνευθειακά και επομένως, και τα τέσσερα σημεία
είναι συνευθειακά και επομένως, και τα τέσσερα σημεία  ανήκουν στην ίδια ευθεία.
ανήκουν στην ίδια ευθεία.
 Από
Από  και
και 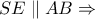



Αλλά, από

 και από
και από 

Από


Από

 και το ισοδύναμο ζητούμενο έχει αποδειχθεί.
και το ισοδύναμο ζητούμενο έχει αποδειχθεί.Κώστας Βήττας.


 και με
και με  προκύπτει ότι τα τρίγωνα
προκύπτει ότι τα τρίγωνα  είναι
είναι  είναι ο ορθοπόλος του
είναι ο ορθοπόλος του  .
.



 και με όμοιο τρόπο προκύπτει ότι
και με όμοιο τρόπο προκύπτει ότι  .
.
 .
.
 ομοκυκλικά και με
ομοκυκλικά και με  σύμφωνα με το
σύμφωνα με το το οποίο είναι το μέσο της
το οποίο είναι το μέσο της  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί.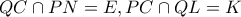

 και
και 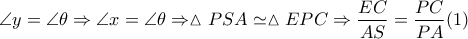
 είναι ισοσκελές τραπέζιο
είναι ισοσκελές τραπέζιο 
 και
και  μέσον της
μέσον της  (αφού
(αφού  )
)
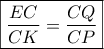
 ορθογωνίου
ορθογωνίου  στο
στο  και τον περίκυκλο στο
και τον περίκυκλο στο  . Η παράλληλη από το
. Η παράλληλη από το  στα
στα 
 έχουμε
έχουμε  ...(1)
...(1) είναι
είναι 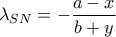 και του
και του  είναι
είναι  άρα λόγω της (1)
άρα λόγω της (1)

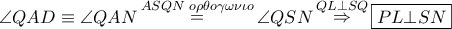
 ισοσκελές τραπέζιο
ισοσκελές τραπέζιο 
 εγγράψιμο
εγγράψιμο
 των πλευρών του
των πλευρών του  αντίστοιχα , τέτοια ώστε το τρίγωνο
αντίστοιχα , τέτοια ώστε το τρίγωνο  να είναι ισόπλευρο.
να είναι ισόπλευρο. .
. του ορθογωνίου του σχήματος είναι οι εστίες της έλλειψης . Υπολογίστε
του ορθογωνίου του σχήματος είναι οι εστίες της έλλειψης . Υπολογίστε , για ποια σχέση των
, για ποια σχέση των 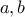 , εξασφαλίζεται η ύπαρξη αυτού του ορθογωνίου και ποιος είναι τότε ο λόγος
, εξασφαλίζεται η ύπαρξη αυτού του ορθογωνίου και ποιος είναι τότε ο λόγος  ;
;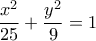
 και
και  τότε
τότε 


 (στην ισότητα προκύπτει τετράγωνο)
(στην ισότητα προκύπτει τετράγωνο)

 διέρχεται από το κέντρο
διέρχεται από το κέντρο  του ορθογωνίου .
του ορθογωνίου . περίκυκλο του
περίκυκλο του  οι ριζικοί άξονες των
οι ριζικοί άξονες των 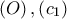 και
και  είναι
είναι  αντίστοιχα, που τέμνονται στο
αντίστοιχα, που τέμνονται στο  .
. που είναι ο
που είναι ο 
 . Σχεδιάζω το ( επίσης ) ορθογώνιο
. Σχεδιάζω το ( επίσης ) ορθογώνιο  . Πώς πρέπει να επιλεγεί
. Πώς πρέπει να επιλεγεί , να ισούται με
, να ισούται με  ;
;
 , απ' όπου προσδιορίζεται η κορυφή
, απ' όπου προσδιορίζεται η κορυφή  και φέρνω κάθετη στην
και φέρνω κάθετη στην  , κλπ.
, κλπ. ορθογωνίου
ορθογωνίου  του
του  , άρα η ελάχιστη απόσταση θα είναι είτε από την κορυφή
, άρα η ελάχιστη απόσταση θα είναι είτε από την κορυφή  ) είτε από την κορυφή
) είτε από την κορυφή  σε σημείο
σε σημείο 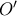 , συμμετρικό του
, συμμετρικό του 
 , (
, ( ακτίνα του πράσινου κύκλου).
ακτίνα του πράσινου κύκλου).  , οπότε:
, οπότε:




