 του σχήματος που αποτελείται από δυο τεταρτοκύκλια
του σχήματος που αποτελείται από δυο τεταρτοκύκλια  ,
,  και το ορθογώνιο
και το ορθογώνιο  από το οποίο έχει αφαιρεθεί το ημικύκλιο
από το οποίο έχει αφαιρεθεί το ημικύκλιο  .
. Να βρεθεί η τιμή της ακτίνας
 ώστε το χωρίο να έχει το μέγιστο εμβαδόν.
ώστε το χωρίο να έχει το μέγιστο εμβαδόν. 2) Αν το χωρίο
 αποτελεί την κάτοψη ενός καναπέ, τότε αυτός ο καναπές μπορεί να περάσει από στροφή
αποτελεί την κάτοψη ενός καναπέ, τότε αυτός ο καναπές μπορεί να περάσει από στροφή  διαδρόμου πλάτους 1. (βλ. animation)
διαδρόμου πλάτους 1. (βλ. animation)
Να δείξετε ότι αν κάποιο χωρίο (οποιουδήποτε σχήματος) έχει εμβαδόν πάνω από
 δεν μπορεί να περάσει από τη στροφή.
δεν μπορεί να περάσει από τη στροφή. Υ.Γ. Το συνημμένο αρχείο geogebra ενδεχομένως να βοηθήσει στην καλύτερη κατανόηση της κίνησης.

 του ιδεατού αυτού σχήματος ονομάζεται σταθερά του καναπέ. Η άσκηση αυτή δείχνει ότι:
του ιδεατού αυτού σχήματος ονομάζεται σταθερά του καναπέ. Η άσκηση αυτή δείχνει ότι: .
. και
και  έχουν σταθερό εμβαδόν το οποίο ισούται με
έχουν σταθερό εμβαδόν το οποίο ισούται με  . Για το εμβαδόν του χωρίου
. Για το εμβαδόν του χωρίου  έχουμε:
έχουμε: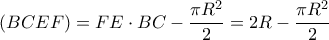
 όπου
όπου 
 παρουσιάζει ολικό μέγιστο στο
παρουσιάζει ολικό μέγιστο στο  το οποίο είναι:
το οποίο είναι:  .
.