
2.

3.
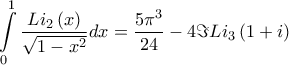
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
pprime έγραψε:2.


 και
και 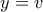 , οπότε
, οπότε  ,
, 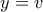 και
και 

![\displaystyle{ = - 2\int\limits_0^1 {{{\left( {{{\arcsin }^2}\left( w \right)} \right)}{'}}\log wdw} = - 2\left[ {{{\arcsin }^2}\left( w \right)\log w} \right]_0^1 + } \displaystyle{ = - 2\int\limits_0^1 {{{\left( {{{\arcsin }^2}\left( w \right)} \right)}{'}}\log wdw} = - 2\left[ {{{\arcsin }^2}\left( w \right)\log w} \right]_0^1 + }](/forum/ext/geomar/texintegr/latexrender/pictures/d9ad1262e8c34bcf74caecd64215d80a.png)
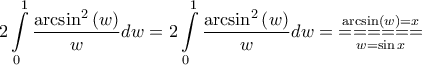
![\displaystyle{ = 2\int\limits_0^{\pi /2} {\frac{{{x^2}}}{{\sin x}}\cos x\;dx} = 2\int\limits_0^{\pi /2} {{x^2}\left( {\log \sin x} \right)'\;dx} = 2\left[ {{x^2}\log \sin x} \right]_0^{\pi /2}} \displaystyle{ = 2\int\limits_0^{\pi /2} {\frac{{{x^2}}}{{\sin x}}\cos x\;dx} = 2\int\limits_0^{\pi /2} {{x^2}\left( {\log \sin x} \right)'\;dx} = 2\left[ {{x^2}\log \sin x} \right]_0^{\pi /2}}](/forum/ext/geomar/texintegr/latexrender/pictures/a401f55e16a4097e7a8cd65360a9d77b.png)
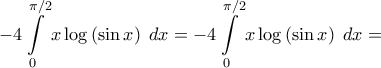


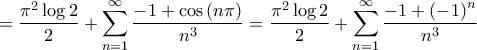

 (έχει αποδειχθεί αρκετές φορές εδώ μέσα).
(έχει αποδειχθεί αρκετές φορές εδώ μέσα).pprime έγραψε:1.
 διότι
διότι 
![\displaystyle{ = \frac{1}{y}\left[ {2\sqrt x - 2\sqrt {1 - x} \arcsin \left( {\sqrt x } \right)} \right]_0^y = \frac{{2\left( {\sqrt y - \sqrt {1 - y} \arcsin \left( {\sqrt y } \right)} \right)}}{y}} \displaystyle{ = \frac{1}{y}\left[ {2\sqrt x - 2\sqrt {1 - x} \arcsin \left( {\sqrt x } \right)} \right]_0^y = \frac{{2\left( {\sqrt y - \sqrt {1 - y} \arcsin \left( {\sqrt y } \right)} \right)}}{y}}](/forum/ext/geomar/texintegr/latexrender/pictures/a44f7b213bf4295a93a064f37c01717f.png)
 διότι
διότι ![\displaystyle{\int\limits_0^1 {\frac{1}{{\sqrt y \sqrt {1 - y} }}dy} \mathop { = = = }\limits^{y = {x^2}} \int\limits_0^1 {\frac{{2x}}{{x\sqrt {1 - {x^2}} }}dx} = 2\left[ {\arcsin \left( x \right)} \right]_0^1 = \pi } \displaystyle{\int\limits_0^1 {\frac{1}{{\sqrt y \sqrt {1 - y} }}dy} \mathop { = = = }\limits^{y = {x^2}} \int\limits_0^1 {\frac{{2x}}{{x\sqrt {1 - {x^2}} }}dx} = 2\left[ {\arcsin \left( x \right)} \right]_0^1 = \pi }](/forum/ext/geomar/texintegr/latexrender/pictures/58d5d80390cc8b74caddfb249294e338.png)
 διότι
διότι 






Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 10 επισκέπτες