η συνάρτηση Γάμμα του Euler. Απoδείξατε ότι
Απλοποίηση τιμών Γάμμα
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
-
Tolaso J Kos
- Δημοσιεύσεις: 5227
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Απλοποίηση τιμών Γάμμα
Έστω η συνάρτηση Γάμμα του Euler. Απoδείξατε ότι
η συνάρτηση Γάμμα του Euler. Απoδείξατε ότιΗ φαντασία είναι σημαντικότερη από τη γνώση !
Λέξεις Κλειδιά:
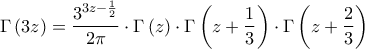
![\displaystyle{\frac{\Gamma \left( \frac{1}{10} \right)}{\Gamma \left( \frac{2}{15} \right)\cdot \Gamma \left( \frac{7}{15} \right)}=\frac{\varphi }{\sqrt[10]{12}\cdot \sqrt{\pi }}}](/forum/ext/geomar/texintegr/latexrender/pictures/e3f4302049f6d652abf6fb26790d01d8.png "\displaystyle{\frac{\Gamma \left( \frac{1}{10} \right)}{\Gamma \left( \frac{2}{15} \right)\cdot \Gamma \left( \frac{7}{15} \right)}=\frac{\varphi }{\sqrt[10]{12}\cdot \sqrt{\pi }}}")
![\displaystyle{\Gamma \left( \frac{2}{5} \right)=\frac{3^{\frac{2}{5}-\frac{1}{2}}}{2\pi }\cdot \Gamma \left( \frac{2}{15} \right)\cdot \Gamma \left( \frac{2}{15}+\frac{1}{3} \right)\cdot \Gamma \left( \frac{2}{15}+\frac{2}{3} \right)=\frac{\Gamma \left( \frac{4}{5} \right)}{2\pi \cdot \sqrt[10]{3}}\cdot \Gamma \left( \frac{2}{15} \right)\cdot \Gamma \left( \frac{7}{15} \right)}](/forum/ext/geomar/texintegr/latexrender/pictures/644896d1ff88dc8083cd832027bac24d.png "\displaystyle{\Gamma \left( \frac{2}{5} \right)=\frac{3^{\frac{2}{5}-\frac{1}{2}}}{2\pi }\cdot \Gamma \left( \frac{2}{15} \right)\cdot \Gamma \left( \frac{2}{15}+\frac{1}{3} \right)\cdot \Gamma \left( \frac{2}{15}+\frac{2}{3} \right)=\frac{\Gamma \left( \frac{4}{5} \right)}{2\pi \cdot \sqrt[10]{3}}\cdot \Gamma \left( \frac{2}{15} \right)\cdot \Gamma \left( \frac{7}{15} \right)}")
![\displaystyle{\frac{\Gamma \left( \frac{1}{10} \right)}{\Gamma \left( \frac{2}{15} \right)\cdot \Gamma \left( \frac{7}{15} \right)}=\frac{\Gamma \left( \frac{1}{10} \right)\cdot \Gamma \left( \frac{4}{5} \right)}{\Gamma \left( \frac{2}{5} \right)}\cdot \frac{1}{2\pi \sqrt[10]{3}}=\frac{\Gamma \left( \frac{1}{10} \right)\cdot \left( \frac{1}{\sqrt[5]{2}\cdot \sqrt{\pi }}\cdot \Gamma \left( \frac{2}{5} \right)\cdot \Gamma \left( \frac{9}{10} \right) \right)}{\Gamma \left( \frac{2}{5} \right)}\cdot \frac{1}{2\pi \sqrt[10]{3}}}](/forum/ext/geomar/texintegr/latexrender/pictures/68ac08b4790f7fc74067e14f00014593.png "\displaystyle{\frac{\Gamma \left( \frac{1}{10} \right)}{\Gamma \left( \frac{2}{15} \right)\cdot \Gamma \left( \frac{7}{15} \right)}=\frac{\Gamma \left( \frac{1}{10} \right)\cdot \Gamma \left( \frac{4}{5} \right)}{\Gamma \left( \frac{2}{5} \right)}\cdot \frac{1}{2\pi \sqrt[10]{3}}=\frac{\Gamma \left( \frac{1}{10} \right)\cdot \left( \frac{1}{\sqrt[5]{2}\cdot \sqrt{\pi }}\cdot \Gamma \left( \frac{2}{5} \right)\cdot \Gamma \left( \frac{9}{10} \right) \right)}{\Gamma \left( \frac{2}{5} \right)}\cdot \frac{1}{2\pi \sqrt[10]{3}}}")
![\displaystyle{=\frac{1}{2\pi \sqrt[10]{3}}\cdot \frac{1}{\sqrt[5]{2}\cdot \sqrt{\pi }}\cdot \Gamma \left( \frac{9}{10} \right)\cdot \Gamma \left( \frac{1}{10} \right)=\frac{1}{2\sqrt[10]{12}\cdot \pi \sqrt{\pi }}\cdot \Gamma \left( 1-\frac{1}{10} \right)\cdot \Gamma \left( \frac{1}{10} \right)}](/forum/ext/geomar/texintegr/latexrender/pictures/fdb6a64e2c976984ce44b056f3ea6780.png "\displaystyle{=\frac{1}{2\pi \sqrt[10]{3}}\cdot \frac{1}{\sqrt[5]{2}\cdot \sqrt{\pi }}\cdot \Gamma \left( \frac{9}{10} \right)\cdot \Gamma \left( \frac{1}{10} \right)=\frac{1}{2\sqrt[10]{12}\cdot \pi \sqrt{\pi }}\cdot \Gamma \left( 1-\frac{1}{10} \right)\cdot \Gamma \left( \frac{1}{10} \right)}")
![\displaystyle{=\frac{1}{2\sqrt[10]{12}\cdot \pi \sqrt{\pi }}\cdot \frac{\pi }{\sin \frac{\pi }{10}}=\frac{1}{2\sqrt[10]{12}\cdot \sqrt{\pi }}\cdot \frac{4}{\sqrt{5}-1}=\frac{1}{\sqrt[10]{12}\cdot \sqrt{\pi }}\cdot \frac{1+\sqrt{5}}{2}=\frac{\varphi }{\sqrt[10]{12}\cdot \sqrt{\pi }}}](/forum/ext/geomar/texintegr/latexrender/pictures/5217b629fbeb3741d5a29131daaacd25.png "\displaystyle{=\frac{1}{2\sqrt[10]{12}\cdot \pi \sqrt{\pi }}\cdot \frac{\pi }{\sin \frac{\pi }{10}}=\frac{1}{2\sqrt[10]{12}\cdot \sqrt{\pi }}\cdot \frac{4}{\sqrt{5}-1}=\frac{1}{\sqrt[10]{12}\cdot \sqrt{\pi }}\cdot \frac{1+\sqrt{5}}{2}=\frac{\varphi }{\sqrt[10]{12}\cdot \sqrt{\pi }}}")
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες