
Παράξενο εναλλασσόμενο άθροισμα
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
- Tolaso J Kos
- Δημοσιεύσεις: 5226
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Παράξενο εναλλασσόμενο άθροισμα
Αποδείξατε ότι


Η φαντασία είναι σημαντικότερη από τη γνώση !


Λέξεις Κλειδιά:
- Γ.-Σ. Σμυρλής
- Δημοσιεύσεις: 578
- Εγγραφή: Κυρ Οκτ 14, 2012 9:47 am
- Τοποθεσία: Λευκωσία, Κύπρος
Re: Παράξενο εναλλασσόμενο άθροισμα
Παρατηροῦμε κατ᾽ ἀρχὰς ὅτι

Ἐδῶ θὰ χρησιμοποιήσω ἕναν τύπο ἕτοιμο

ἀπ᾽ὅπου τὸ ζητούμενο προκύπτει ἄμεσα.
Ὁ ἀνωτέρω τύπος προκύπτει ὁλοκληρώνοντας τὴν συνάρτηση

κατά μῆκος τοῦ τετραγώνου τὸ ὁποῖο ὁρίζεται ἀπὸ τὰ σημεῖα
τὸ ὁποῖο ὁρίζεται ἀπὸ τὰ σημεῖα  , ἐφαρμόζοντας τὸν ὁλοκληρωτικὸ τύπο ὑπολοίπων Cauchy, καθὼς
, ἐφαρμόζοντας τὸν ὁλοκληρωτικὸ τύπο ὑπολοίπων Cauchy, καθὼς  .
.

Ἐδῶ θὰ χρησιμοποιήσω ἕναν τύπο ἕτοιμο

ἀπ᾽ὅπου τὸ ζητούμενο προκύπτει ἄμεσα.
Ὁ ἀνωτέρω τύπος προκύπτει ὁλοκληρώνοντας τὴν συνάρτηση

κατά μῆκος τοῦ τετραγώνου
 τὸ ὁποῖο ὁρίζεται ἀπὸ τὰ σημεῖα
τὸ ὁποῖο ὁρίζεται ἀπὸ τὰ σημεῖα  , ἐφαρμόζοντας τὸν ὁλοκληρωτικὸ τύπο ὑπολοίπων Cauchy, καθὼς
, ἐφαρμόζοντας τὸν ὁλοκληρωτικὸ τύπο ὑπολοίπων Cauchy, καθὼς  .
.- Σεραφείμ
- Επιμελητής
- Δημοσιεύσεις: 1872
- Εγγραφή: Τετ Μάιος 20, 2009 9:14 am
- Τοποθεσία: Θεσσαλονίκη - Γιάννενα
Re: Παράξενο εναλλασσόμενο άθροισμα
Κάπως διαφορετικά .. ΕπειδήTolaso J Kos έγραψε:Αποδείξατε ότι
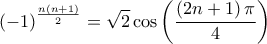 έχουμε
έχουμε 




 . Όμως από εδώ http://functions.wolfram.com/ZetaFuncti ... owAll.html γνωρίζουμε ότι
. Όμως από εδώ http://functions.wolfram.com/ZetaFuncti ... owAll.html γνωρίζουμε ότι  , οπότε
, οπότε
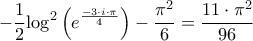 καθώς και
καθώς και 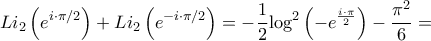

Τελικά

Σεραφείμ Τσιπέλης
- Tolaso J Kos
- Δημοσιεύσεις: 5226
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Παράξενο εναλλασσόμενο άθροισμα
Χωρίς μιγαδική το έχουμε δει εδώ. Ουσιαστικά πρόκειται τη συνάρτησηΓ.-Σ. Σμυρλής έγραψε:
Ἐδῶ θὰ χρησιμοποιήσω ἕναν τύπο ἕτοιμο
ἀπ᾽ὅπου τὸ ζητούμενο προκύπτει ἄμεσα.
 . Οπότε παραγωγίζοντας παίρνουμε το ζητούμενο.
. Οπότε παραγωγίζοντας παίρνουμε το ζητούμενο.Η φαντασία είναι σημαντικότερη από τη γνώση !


- Tolaso J Kos
- Δημοσιεύσεις: 5226
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Παράξενο εναλλασσόμενο άθροισμα
Για το αρχικό άθροισμα κάπως διαφορετικά. Παρατηρούμε ότι:
![\displaystyle{\sum_{k=0}^{\infty}\dfrac{(-1)^{\frac{k(k+1)}{2}}}{(2k+1)^2} = \sum_{k=0}^{\infty} \left [\frac1{(8 k+1)^2} – \frac1{(8 k+3)^2} – \frac1{(8 k+5)^2}+\frac1{(8 k+7)^2} \right ]} \displaystyle{\sum_{k=0}^{\infty}\dfrac{(-1)^{\frac{k(k+1)}{2}}}{(2k+1)^2} = \sum_{k=0}^{\infty} \left [\frac1{(8 k+1)^2} – \frac1{(8 k+3)^2} – \frac1{(8 k+5)^2}+\frac1{(8 k+7)^2} \right ]}](/forum/ext/geomar/texintegr/latexrender/pictures/a42d7619e65e76cf5c577cc0dc79c187.png) και απλά εφαρμόζουμε
και απλά εφαρμόζουμε  μαζί με τον ανακλαστικό τύπο αυτής.
μαζί με τον ανακλαστικό τύπο αυτής.
![\displaystyle{\sum_{k=0}^{\infty}\dfrac{(-1)^{\frac{k(k+1)}{2}}}{(2k+1)^2} = \sum_{k=0}^{\infty} \left [\frac1{(8 k+1)^2} – \frac1{(8 k+3)^2} – \frac1{(8 k+5)^2}+\frac1{(8 k+7)^2} \right ]} \displaystyle{\sum_{k=0}^{\infty}\dfrac{(-1)^{\frac{k(k+1)}{2}}}{(2k+1)^2} = \sum_{k=0}^{\infty} \left [\frac1{(8 k+1)^2} – \frac1{(8 k+3)^2} – \frac1{(8 k+5)^2}+\frac1{(8 k+7)^2} \right ]}](/forum/ext/geomar/texintegr/latexrender/pictures/a42d7619e65e76cf5c577cc0dc79c187.png) και απλά εφαρμόζουμε
και απλά εφαρμόζουμε  μαζί με τον ανακλαστικό τύπο αυτής.
μαζί με τον ανακλαστικό τύπο αυτής.Η φαντασία είναι σημαντικότερη από τη γνώση !


- Σεραφείμ
- Επιμελητής
- Δημοσιεύσεις: 1872
- Εγγραφή: Τετ Μάιος 20, 2009 9:14 am
- Τοποθεσία: Θεσσαλονίκη - Γιάννενα
Re: Παράξενο εναλλασσόμενο άθροισμα
Έτσι το ξεκίνησα αρχικά, αλλά τριγωνομετρικά δεν έκλεινε με τίποτα. Μαζεύεται βέβαια με τρίγαμα, αλλά μου φάνηκαν σκληρές οι πράξεις μέσω ανακλαστικών τύπων ... ωραίο θέμα.Tolaso J Kos έγραψε:Για το αρχικό άθροισμα κάπως διαφορετικά. Παρατηρούμε ότι:
και απλά εφαρμόζουμε
μαζί με τον ανακλαστικό τύπο αυτής.
Σεραφείμ Τσιπέλης
- Tolaso J Kos
- Δημοσιεύσεις: 5226
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Παράξενο εναλλασσόμενο άθροισμα
Χμμ.. είναι αλλά δε τις έχω κάνει με το χέρι !!Σεραφείμ έγραψε:.... αλλά μου φάνηκαν σκληρές οι πράξεις μέσω ανακλαστικών τύπων ....
Η φαντασία είναι σημαντικότερη από τη γνώση !


Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 11 επισκέπτες

