![g_n:[0, 1] \longrightarrow \mathbb{R} g_n:[0, 1] \longrightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/9601d534c178598bd12bc53243fc7d74.png) που ορίζονται ως
που ορίζονται ως ![g_n(x)=\begin{cases}\dfrac{x^{\frac{1}{n}}\log(1+x)}{x\,(1+x^{\frac{2}{n}})^{\frac{3}{2}}}\,,& x\in(0,1]\\
0\,,& x=0\end{cases}\,,\quad n\in\mathbb{N}\,. g_n(x)=\begin{cases}\dfrac{x^{\frac{1}{n}}\log(1+x)}{x\,(1+x^{\frac{2}{n}})^{\frac{3}{2}}}\,,& x\in(0,1]\\
0\,,& x=0\end{cases}\,,\quad n\in\mathbb{N}\,.](/forum/ext/geomar/texintegr/latexrender/pictures/bce846c3fe385b1d2c4c1dab6e60884a.png)
- Να εξετασθεί αν η ακολουθία
 συγκλίνει ομοιόμορφα στο
συγκλίνει ομοιόμορφα στο ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) .
. - Να υπολογισθεί το
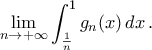
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
![g_n:[0, 1] \longrightarrow \mathbb{R} g_n:[0, 1] \longrightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/9601d534c178598bd12bc53243fc7d74.png) που ορίζονται ως
που ορίζονται ως ![g_n(x)=\begin{cases}\dfrac{x^{\frac{1}{n}}\log(1+x)}{x\,(1+x^{\frac{2}{n}})^{\frac{3}{2}}}\,,& x\in(0,1]\\
0\,,& x=0\end{cases}\,,\quad n\in\mathbb{N}\,. g_n(x)=\begin{cases}\dfrac{x^{\frac{1}{n}}\log(1+x)}{x\,(1+x^{\frac{2}{n}})^{\frac{3}{2}}}\,,& x\in(0,1]\\
0\,,& x=0\end{cases}\,,\quad n\in\mathbb{N}\,.](/forum/ext/geomar/texintegr/latexrender/pictures/bce846c3fe385b1d2c4c1dab6e60884a.png)
 συγκλίνει ομοιόμορφα στο
συγκλίνει ομοιόμορφα στο ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) .
.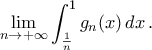

i)grigkost έγραψε:Έστω η ακολουθία συναρτήσεωνπου ορίζονται ως
![g_n(x)=\begin{cases}\dfrac{x^{\frac{1}{n}}\log(1+x)}{x\,(1+x^{\frac{2}{n}})^{\frac{3}{2}}}\,,& x\in(0,1]\\
0\,,& x=0\end{cases}\,,\quad n\in\mathbb{N}\,. g_n(x)=\begin{cases}\dfrac{x^{\frac{1}{n}}\log(1+x)}{x\,(1+x^{\frac{2}{n}})^{\frac{3}{2}}}\,,& x\in(0,1]\\
0\,,& x=0\end{cases}\,,\quad n\in\mathbb{N}\,.](/forum/ext/geomar/texintegr/latexrender/pictures/bce846c3fe385b1d2c4c1dab6e60884a.png)
- Να εξετασθεί αν η ακολουθία
συγκλίνει ομοιόμορφα στο
.
- Να υπολογισθεί το
 είναι συνεχής.
είναι συνεχής. έχουμε
έχουμε 
 προκύπτει
προκύπτει 
 για
για 



![[\epsilon ,1],\epsilon > 0 [\epsilon ,1],\epsilon > 0](/forum/ext/geomar/texintegr/latexrender/pictures/084bbf9e17504f7e6edc68b8c0baf602.png) και να κάνουμε κοψίματα ραψίματα στα ολοκληρώματα.
και να κάνουμε κοψίματα ραψίματα στα ολοκληρώματα.

 είναι ομοιόμορφα φραγμένη. Συγκεκριμένα, υπάρχει
είναι ομοιόμορφα φραγμένη. Συγκεκριμένα, υπάρχει 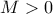 , έτσι ώστε
, έτσι ώστε ![n\in\mathbb{N}\,,\; x\in[0,1] n\in\mathbb{N}\,,\; x\in[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/555ff0cba2366e6b137e8a0743549a23.png) :
:


Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες