 συμβολίζεται ο διλογάριθμος. Δειχθήτω:
συμβολίζεται ο διλογάριθμος. Δειχθήτω:
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
 συμβολίζεται ο διλογάριθμος. Δειχθήτω:
συμβολίζεται ο διλογάριθμος. Δειχθήτω:

Σχόλιο : από εδώ http://functions.wolfram.com/ZetaFuncti ... owAll.html γνωρίζουμε ότιTolaso J Kos έγραψε:Δειχθήτω:
 ,
, 


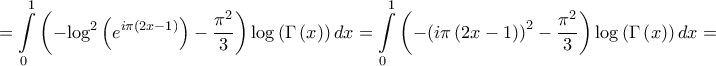

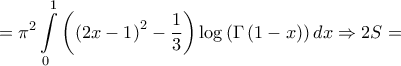




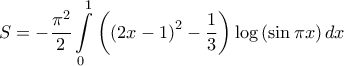 . Όμως
. Όμως  (αποδείχθηκε πολλαπλώς)
(αποδείχθηκε πολλαπλώς) . Άρα
. Άρα 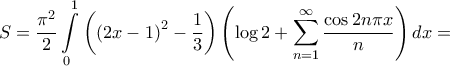


 (στοιχειώδες) και τελικά
(στοιχειώδες) και τελικά 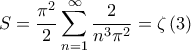
 τη ταυτότητα
τη ταυτότητα Τότε έχουμε διαδοχικά:
Τότε έχουμε διαδοχικά:
 Αφήνεται ως άσκηση στον αναγνώστη. Φυσικά το άθροισμα των πολυλογαρίθμων πέφτει σε κάτι στοιχειώδες αφού για παράδειγμα ισχύει
Αφήνεται ως άσκηση στον αναγνώστη. Φυσικά το άθροισμα των πολυλογαρίθμων πέφτει σε κάτι στοιχειώδες αφού για παράδειγμα ισχύει  όπου με κατάλληλο manipulation και ολοκλήρωση παίρνουμε το τύπο ο οποίος δε περιέχει πολυλογαρίθμους.
όπου με κατάλληλο manipulation και ολοκλήρωση παίρνουμε το τύπο ο οποίος δε περιέχει πολυλογαρίθμους.  Πρόκειται για τους συντελεστές Fourier
Πρόκειται για τους συντελεστές Fourier  του αναπτύγματος
του αναπτύγματος 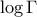 . Δηλαδή
. Δηλαδή

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες