Ασκήσεις στην Ανάλυση!
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
- Tolaso J Kos
- Δημοσιεύσεις: 5226
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Ασκήσεις στην Ανάλυση!
Άσκηση 8
α.Δώστε παράδειγμα δείχνοντας ότι η τομή απείρων ανοιχτών συνόλων μπορεί να μην είναι ανοιχτό σύνολο.
β.Δώστε παράδειγμα δείχνοντας ότι η ένωση απείρων κλειστών συνόλων μπορεί να μην είναι κλειστό σύνολο.
α.Δώστε παράδειγμα δείχνοντας ότι η τομή απείρων ανοιχτών συνόλων μπορεί να μην είναι ανοιχτό σύνολο.
β.Δώστε παράδειγμα δείχνοντας ότι η ένωση απείρων κλειστών συνόλων μπορεί να μην είναι κλειστό σύνολο.
Η φαντασία είναι σημαντικότερη από τη γνώση !


-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Ασκήσεις στην Ανάλυση!
Παραείναι κοινές και απλές ασκήσεις για να αξίζουν τον χώρο στοTolaso J Kos έγραψε:Άσκηση 8
α.Δώστε παράδειγμα δείχνοντας ότι η τομή απείρων ανοιχτών συνόλων μπορεί να μην είναι ανοιχτό σύνολο.
β.Δώστε παράδειγμα δείχνοντας ότι η ένωση απείρων κλειστών συνόλων μπορεί να μην είναι κλειστό σύνολο.
α)
![\displaystyle{ \bigcap _{n=0}^{\infty} \left ( -\frac {1}{n} , \, 1+\frac {1}{n} \right ) = [0, \, 1]} \displaystyle{ \bigcap _{n=0}^{\infty} \left ( -\frac {1}{n} , \, 1+\frac {1}{n} \right ) = [0, \, 1]}](/forum/ext/geomar/texintegr/latexrender/pictures/e91f3605c1cc8eaf8435f52b66456134.png)
β)
![\displaystyle{ \bigcup _{n=0}^{\infty} \left [\frac {1}{n} , \, 1-\frac {1}{n} \right ] = (0, \, 1)} \displaystyle{ \bigcup _{n=0}^{\infty} \left [\frac {1}{n} , \, 1-\frac {1}{n} \right ] = (0, \, 1)}](/forum/ext/geomar/texintegr/latexrender/pictures/8f5f73206d81fb5b4b43b80b6e239b94.png)
-
sokratis lyras
- Δημοσιεύσεις: 711
- Εγγραφή: Σάβ Μαρ 05, 2011 9:13 pm
Re: Ασκήσεις στην Ανάλυση!
Για το α) παίρνουμε 2 θετικές ακολουθίες που συγκλίνουν στοTolaso J Kos έγραψε:Άσκηση 8
α.Δώστε παράδειγμα δείχνοντας ότι η τομή απείρων ανοιχτών συνόλων μπορεί να μην είναι ανοιχτό σύνολο.
β.Δώστε παράδειγμα δείχνοντας ότι η ένωση απείρων κλειστών συνόλων μπορεί να μην είναι κλειστό σύνολο.
 ,τις
,τις  και
και  .H τομή των
.H τομή των  προφανώς δεν είναι ανοιχτό.
προφανώς δεν είναι ανοιχτό.Για το β) ας πάρουμε οποιοδήποτε
![[a_n,k] [a_n,k]](/forum/ext/geomar/texintegr/latexrender/pictures/f5557d5b5aa5016c482a84b989665ab1.png) όπου η
όπου η  να είναι φθίνουσα και να συγκλίνει όπου να ναι, κάτω από το
να είναι φθίνουσα και να συγκλίνει όπου να ναι, κάτω από το  .
.-
sokratis lyras
- Δημοσιεύσεις: 711
- Εγγραφή: Σάβ Μαρ 05, 2011 9:13 pm
Re: Ασκήσεις στην Ανάλυση!
Άσκηση 9
Έστω μετρικός χώρος, και έστω
μετρικός χώρος, και έστω  υποσύνολο του
υποσύνολο του  .
.
Να δείξετε ότι το είναι πυκνό στον
είναι πυκνό στον  αν και μόνο αν για κάθε
αν και μόνο αν για κάθε  συνεχή ισχύει η συνεπαγωγή:
συνεχή ισχύει η συνεπαγωγή:  για κάθε
για κάθε 
Έστω
 μετρικός χώρος, και έστω
μετρικός χώρος, και έστω  υποσύνολο του
υποσύνολο του  .
.Να δείξετε ότι το
 είναι πυκνό στον
είναι πυκνό στον  αν και μόνο αν για κάθε
αν και μόνο αν για κάθε  συνεχή ισχύει η συνεπαγωγή:
συνεχή ισχύει η συνεπαγωγή:  για κάθε
για κάθε 
Re: Ασκήσεις στην Ανάλυση!
Μιχάλη ευχαριστώ για την βοήθεια, αν και για το δεύτερο αντιπαράδειγμα δεν είμαι σίγουρος ότι το κατάλαβα, με την πρώτη ευκαιρία θα το δω πιο προσεκτικά. Έχω βρεί δυο ακόμη αντιπαραδείγματα και θα ήθελα τη γνώμη σου γι΄αυτά.Mihalis_Lambrou έγραψε:Άλλο αντιπαράδειγμα (στην πραγματικότητα χρησιμοποιεί την ίδια ιδέα με το προηγούμενο, αλλά είναι ντυμένο αλλιώς):kgeo67 έγραψε:Ασκηση 7
Η έννοια του ολικά φραγμένου συνόλου διατηρείται από τους ομοιομορφισμούς;
Εξετάζουμε τομε την συνήθη μετρική και, κατόπιν, με την μετρική
.
To πρώτο είναι ολικά φραγμένο (άμεσο) αλλά όχι το δεύτερο. Ένας γρήγορος τρόπος να το διαπιστώσουμε είναι η παρατήρηση ότι ο δεύτερος είναι ισομετρικός με τομέσω της
αλλά, φυσικά, το
δεν είναι ολικά φραγμένο ως μη φραγμένο.
Φιλικά,
Μιχάλης
Στο πρώτο από αυτά έχω θεωρήσει τη συνάρτηση
 με
με  η οποία είναι ομοιομορφισμός, το
η οποία είναι ομοιομορφισμός, το  ολικά φραγμένο ενώ το
ολικά φραγμένο ενώ το 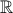 οχι, ενώ στο δεύτερο τη συνάρτηση
οχι, ενώ στο δεύτερο τη συνάρτηση 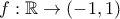 με
με 
Ζητώ προκαταβολικά συγγνώμη για τυχόν λάθη στη γραφή μου, είναι η πρωτη φορά που γράφω σε

Κωνσταντίνος Γεωργίου
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Ασκήσεις στην Ανάλυση!
sokratis lyras έγραψε:Άσκηση 9
Έστωμετρικός χώρος, και έστω
υποσύνολο του
.
Να δείξετε ότι τοείναι πυκνό στον
αν και μόνο αν για κάθε
συνεχή ισχύει η συνεπαγωγή:
για κάθε
 . Αν
. Αν  πυκνό και
πυκνό και  υπάρχει ακολουθία
υπάρχει ακολουθία  με
με  . Αλλά τότε
. Αλλά τότε  .
. . Με αντιθετοαντιστροφή: Αν
. Με αντιθετοαντιστροφή: Αν  μη πυκνό τότε υπάρχει
μη πυκνό τότε υπάρχει  με
με  . Παρατηρούμε τότε ότι η
. Παρατηρούμε τότε ότι η  είναι μη μηδενική με
είναι μη μηδενική με  και, ως γνωστόν (και απλό), είναι συνεχής. Δηλαδή δεν ισχύει η συνεπαγωγή
και, ως γνωστόν (και απλό), είναι συνεχής. Δηλαδή δεν ισχύει η συνεπαγωγή  για κάθε
για κάθε  .
. Φιλικά,
Μιχάλης
-
sokratis lyras
- Δημοσιεύσεις: 711
- Εγγραφή: Σάβ Μαρ 05, 2011 9:13 pm
Re: Ασκήσεις στην Ανάλυση!
Ας το δυσκολέψουμε λίγο :
Άσκηση 10
Έστω άπειρες φορές παραγωγίσιμη.Αν για κάθε
άπειρες φορές παραγωγίσιμη.Αν για κάθε  υπάρχει
υπάρχει  ώστε για κάθε
ώστε για κάθε  να ισχύει
να ισχύει  , να δείξετε ότι η
, να δείξετε ότι η  είναι πολυώνυμο.
είναι πολυώνυμο.
Άσκηση 11
Έστω συμπαγής χώρος και
συμπαγής χώρος και  συνάρτηση έτσι ώστε
συνάρτηση έτσι ώστε  .
.
Να δείξετε ότι η είναι ισομετρία.
είναι ισομετρία.
Μπορούμε να πούμε ότι ισχύει το ίδιο αποτέλεσμα αν ισχύει η ανάποδη ανισότητα?
Άσκηση 10
Έστω
 άπειρες φορές παραγωγίσιμη.Αν για κάθε
άπειρες φορές παραγωγίσιμη.Αν για κάθε  υπάρχει
υπάρχει  ώστε για κάθε
ώστε για κάθε  να ισχύει
να ισχύει  , να δείξετε ότι η
, να δείξετε ότι η  είναι πολυώνυμο.
είναι πολυώνυμο.Άσκηση 11
Έστω
 συμπαγής χώρος και
συμπαγής χώρος και  συνάρτηση έτσι ώστε
συνάρτηση έτσι ώστε  .
.Να δείξετε ότι η
 είναι ισομετρία.
είναι ισομετρία.Μπορούμε να πούμε ότι ισχύει το ίδιο αποτέλεσμα αν ισχύει η ανάποδη ανισότητα?
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Ασκήσεις στην Ανάλυση!
Έχουμε δει και τις δύο. Η πρώτη βασίζεται στο θεώρημα Baire (δεν την βρίσκω στοsokratis lyras έγραψε:Ας το δυσκολέψουμε λίγο :
Άσκηση 10
Έστωάπειρες φορές παραγωγίσιμη.Αν για κάθε
υπάρχει
ώστε για κάθε
να ισχύει
, να δείξετε ότι η
είναι πολυώνυμο.
Άσκηση 11
Έστωσυμπαγής χώρος και
συνάρτηση έτσι ώστε
.
Να δείξετε ότι ηείναι ισομετρία.
Μπορούμε να πούμε ότι ισχύει το ίδιο αποτέλεσμα αν ισχύει η ανάποδη ανισότητα?
Για το δεύτερο βλέπε εδώ.
Φιλικά,
Μιχάλης
Υ.Γ.
Όχι:sokratis lyras έγραψε: Μπορούμε να πούμε ότι ισχύει το ίδιο αποτέλεσμα αν ισχύει η ανάποδη ανισότητα?
 στο
στο ![[0, \, 1] [0, \, 1]](/forum/ext/geomar/texintegr/latexrender/pictures/26ccf70f76413c8a68f895ead68d9cea.png)
-
sokratis lyras
- Δημοσιεύσεις: 711
- Εγγραφή: Σάβ Μαρ 05, 2011 9:13 pm
Re: Ασκήσεις στην Ανάλυση!
Τι πρέπει να προσθέσουμε για να ισχύει?(εύκολο)Mihalis_Lambrou έγραψε:
Όχι:στο
-
stranton
- Επιμελητής
- Δημοσιεύσεις: 679
- Εγγραφή: Πέμ Ιουν 25, 2009 5:00 pm
- Τοποθεσία: Σπάρτη
- Επικοινωνία:
Re: Ασκήσεις στην Ανάλυση!
Πρέπει να προσθέσουμε να είναι ηsokratis lyras έγραψε:Τι πρέπει να προσθέσουμε για να ισχύει?(εύκολο)
 1-1 και επί.
1-1 και επί.Τότε θα ορίζεται η
 και για κάθε
και για κάθε  θα είναι:
θα είναι: 
Τότε η
 θα είναι ισομετρία, οπότε και η
θα είναι ισομετρία, οπότε και η  θα είναι ισομετρία.
θα είναι ισομετρία.Στράτης Αντωνέας
-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: Ασκήσεις στην Ανάλυση!
Γειά σας.Η ασκήση 11 βρισκέται στο Real Analysis του Carothers με υπόδειξη.(η απόδειξη είναι πιο ''απλή'' από την απόδειξη του Μιχάλη Λάμπρου)
-
stranton
- Επιμελητής
- Δημοσιεύσεις: 679
- Εγγραφή: Πέμ Ιουν 25, 2009 5:00 pm
- Τοποθεσία: Σπάρτη
- Επικοινωνία:
Re: Ασκήσεις στην Ανάλυση!
Άσκηση 12
Έστω σύνολο θετικών πραγματικών αριθμών με
σύνολο θετικών πραγματικών αριθμών με 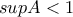 . Υποθέτουμε ότι το
. Υποθέτουμε ότι το  έχει την ιδιότητα:
έχει την ιδιότητα:
αν και
και  , τότε
, τότε  . Να αποδείξετε ότι
. Να αποδείξετε ότι  .
.
Έστω
 σύνολο θετικών πραγματικών αριθμών με
σύνολο θετικών πραγματικών αριθμών με 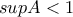 . Υποθέτουμε ότι το
. Υποθέτουμε ότι το  έχει την ιδιότητα:
έχει την ιδιότητα:αν
 και
και  , τότε
, τότε  . Να αποδείξετε ότι
. Να αποδείξετε ότι  .
.Στράτης Αντωνέας
Re: Ασκήσεις στην Ανάλυση!
Καλησπέρα!!stranton έγραψε:Άσκηση 12
Έστωσύνολο θετικών πραγματικών αριθμών με
. Υποθέτουμε ότι το
έχει την ιδιότητα:
ανκαι
, τότε
. Να αποδείξετε ότι
.
Κάνω μια προσπάθεια αλλά δεν ξέρω αν είναι σωστή, αν μπορει καποιος να την κοιτάξει και να μου πει.
Προφανώς
 .
.Έστω τώρα το χ δεν ανήκει στο Α. Τότε μπορούμε να βρούμε μια γνησίως αύξουσα ακολουθία
 με
με  .
.Απόδειξη: Τώρα προκύπτει ότι
 , αφού
, αφού  γν.αύξουσα.
γν.αύξουσα.Άρα
 και αφού τα όρια ακολουθιών διατηρούν τη διάταξη προκύπτει ότι:
και αφού τα όρια ακολουθιών διατηρούν τη διάταξη προκύπτει ότι:  , καθώς
, καθώς  , άτοπο.
, άτοπο.Συνεπώς
 .
.ΥΓ.Πώς γράφεται το "δεν ανήκει" στο latex?
- Tolaso J Kos
- Δημοσιεύσεις: 5226
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Ασκήσεις στην Ανάλυση!
opener έγραψε:
ΥΓ.Πώς γράφεται το "δεν ανήκει" στο latex?
Κώδικας: Επιλογή όλων
x \notin A .
.Η φαντασία είναι σημαντικότερη από τη γνώση !


-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Ασκήσεις στην Ανάλυση!
sokratis lyras έγραψε: Άσκηση 10
Έστωάπειρες φορές παραγωγίσιμη.Αν για κάθε
υπάρχει
ώστε για κάθε
να ισχύει
, να δείξετε ότι η
είναι πολυώνυμο.
Από τα Γιάννενα εν αναμονή του τεράστιου σε όγκο Σεμιναρίου της ΟΕΦΕ, βλέπεMihalis_Lambrou έγραψε: Έχουμε δει και τις δύο. Η πρώτη βασίζεται στο θεώρημα Baire (δεν την βρίσκω στοαυτή την στιγμή και επειδή αύριο έχω ταξίδι, δεν έχω πολύ χρόνο να ψάξω. Θα χαρώ να εντοπίσει κάποιος το σχετικό ποστ).
για το παραπάνω στα
viewtopic.php?f=9&t=5407&p=30643&hilit=Baire#p30643
viewtopic.php?f=9&t=3078&p=17885#p17885
Μ.
viewtopic.php?f=9&t=3078&p=17569&hilit=Taylor#p17569
Re: Ασκήσεις στην Ανάλυση!
Μια άσκηση ώστε να μη πεθάνει το τόπικ!
Δε ξέρω αν κάνει για το συγκεκριμενο θέμα αλλα όπως και να έχει, νομίζω είναι ενδιαφέρουσα:
Άσκηση 13
Να εξετάσετε ως προς τη σύγκλιση την ,
,  .
.
Δε ξέρω αν κάνει για το συγκεκριμενο θέμα αλλα όπως και να έχει, νομίζω είναι ενδιαφέρουσα:
Άσκηση 13
Να εξετάσετε ως προς τη σύγκλιση την
 ,
,  .
.- AlexandrosG
- Δημοσιεύσεις: 466
- Εγγραφή: Πέμ Οκτ 22, 2009 5:31 am
- Επικοινωνία:
Re: Ασκήσεις στην Ανάλυση!
Μια αντιμετώπιση .opener έγραψε:Μια άσκηση ώστε να μη πεθάνει το τόπικ!
Δε ξέρω αν κάνει για το συγκεκριμενο θέμα αλλα όπως και να έχει, νομίζω είναι ενδιαφέρουσα:
Άσκηση 13
Να εξετάσετε ως προς τη σύγκλιση την,
.
Από την ανισότητα εδώ παίρνουμε ότι για κάθε

 .
. Άρα το όριο είναι
 .
.Υπάρχει μία πιο κλασική αντιμετώπιση. Το αφήνω σαν άσκηση να βρεθούν διαφορετικές λύσεις.
- Tolaso J Kos
- Δημοσιεύσεις: 5226
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Ασκήσεις στην Ανάλυση!
Η λύση που έχω για αυτό (για το όριο) είναι με αριθμούςopener έγραψε:Μια άσκηση ώστε να μη πεθάνει το τόπικ!
Δε ξέρω αν κάνει για το συγκεκριμενο θέμα αλλα όπως και να έχει, νομίζω είναι ενδιαφέρουσα:
Άσκηση 13
Να εξετάσετε ως προς τη σύγκλιση την,
.
 . Κάποτε την είχα δει αυτή την άσκηση και μου χει κάνει εντύπωση. Γράφω τη λύση για ποικιλία.
. Κάποτε την είχα δει αυτή την άσκηση και μου χει κάνει εντύπωση. Γράφω τη λύση για ποικιλία.Έστω
 . Αυτό είναι πολυώνυμο βαθμού
. Αυτό είναι πολυώνυμο βαθμού  και δίδεται του τύπου: (είναι γνωστός ο τύπος)
και δίδεται του τύπου: (είναι γνωστός ο τύπος)
όπου
 οι αριθμοί
οι αριθμοί  .
.Οπότε:

αφού
 από όπου το ζητούμενο.
από όπου το ζητούμενο. Σαφώς είναι πιο δύσκολη λύση από τη πάνω που έδωσε ο Αλέξανδρος, αλλά μου είχε αρέσει. Υπάρχουν βέβαια αρκετές λύσεις για αυτή. Μία άλλη που θυμάμαι είναι με ολοκλήρωμα:
Γράφουμε:
 .
.Οπότε το όριο γράφεται:

Ελπίζω να μην έχω μπερδέψει τους συμβολισμούς.. μιας και είναι περασμένη η ώρα...
____________________________________________________________________________________________
Ένα παρεμφερές πρόβλημα (όριο) είναι και το εξής:
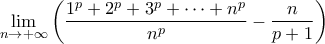
Η φαντασία είναι σημαντικότερη από τη γνώση !


- Tolaso J Kos
- Δημοσιεύσεις: 5226
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Ασκήσεις στην Ανάλυση!
Μία που μου έκανε εντύπωση
Άσκηση 14
Έστω τέτοια ώστε:
τέτοια ώστε:  .
.
Να υπολογίσετε το όριο:

Άσκηση 14
Έστω
 τέτοια ώστε:
τέτοια ώστε:  .
.Να υπολογίσετε το όριο:

Η φαντασία είναι σημαντικότερη από τη γνώση !


Re: Ασκήσεις στην Ανάλυση!
Ένα ωραίο συμπέρασμα της Συναρτησιακής Ανάλυσης που προκύπτει από την άσκηση αυτή είναι το ακόλουθο.sokratis lyras έγραψε:Άσκηση 9
Έστωμετρικός χώρος, και έστω
υποσύνολο του
.
Να δείξετε ότι τοείναι πυκνό στον
αν και μόνο αν για κάθε
συνεχή ισχύει η συνεπαγωγή:
για κάθε
Αν
 είναι χώρος με νόρμα και
είναι χώρος με νόρμα και 
είναι μια συνεχής και μη-μηδενική
 - γραμμική απεικόνιση, τότε ο πυρήνας αυτής,
- γραμμική απεικόνιση, τότε ο πυρήνας αυτής, δεν είναι πυκνό υποσύνολο του μετρικού χώρου
δεν είναι πυκνό υποσύνολο του μετρικού χώρου 
όπου
 , η επαγόμενη, από την νόρμα του χώρου, μετρική.
, η επαγόμενη, από την νόρμα του χώρου, μετρική.Έτσι, αν συμβολίσουμε με
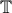 την τοπολογία που προέρεχται από τη μετρική
την τοπολογία που προέρεχται από τη μετρική  ,
,τότε έχουμε την ισχύ της ισοδυναμίας :

όπου
 είναι το σύνολο όλων των γραμμικών και συνεχών απεικονίσεων από το
είναι το σύνολο όλων των γραμμικών και συνεχών απεικονίσεων από το στο
στο  .
.Αν θέσουμε
 και
και  ,
,τότε η συνάρτηση

είναι ασυνεχής. Επίσης, δεν θα μπορούσε να είναι συνεχής και από το γεγονός ότι :
 .
.Ίσως ξέφυγα από το πνεύμα του θέματος αλλά, νομίζω ήταν ωραία συμπεράσματα.
Παπαπέτρος Ευάγγελος
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Google [Bot] και 10 επισκέπτες

![a_1 \in ( x-1, x ] \cap A a_1 \in ( x-1, x ] \cap A](/forum/ext/geomar/texintegr/latexrender/pictures/6cde0dcd71e4866a1d59735538e3725a.png) και αφού το χ δεν ανήκει στο Α, το
και αφού το χ δεν ανήκει στο Α, το  δεν μπορεί να είναι άνω φράγμα άρα
δεν μπορεί να είναι άνω φράγμα άρα  .
. .
. υπάρχει
υπάρχει ![a_{k+1} \in (x-\epsilon ,x] \cap A a_{k+1} \in (x-\epsilon ,x] \cap A](/forum/ext/geomar/texintegr/latexrender/pictures/7ddb565b2239a76e034b3d380d40af4c.png) .Όπως πριν το διάστημα είναι ανοιχτό και άρα:
.Όπως πριν το διάστημα είναι ανοιχτό και άρα: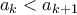 και
και 