Κοτρώνης Αναστάσιος έγραψε:...για όσους με παίζουν...
Αναστάση, άκρως ενδιαφέροντα και δύσκολα τα προβλήματα που μας βάζεις αλλά έχουν ιδιαίτερα επίπονο γράψιμμο (που εμένα με αποτρέπει παρά την χαρά της ενασχόλησης με τις πολύ ωραίες αυτές ασκήσεις).
Από ότι παρατηρώ μένουν άλυτες οι παρακάτω. Έχω λύσεις για μερικές από αυτές και επίσης έχω εναλλακτικές λύσεις σε μερικές ήδη λυμένες αλλά για την ώρα θα καταγράψω μόνο την 5).
Κοτρώνης Αναστάσιος έγραψε:

Αθροισθήτω:

, όπου

.

Έστω
![\displaystyle{f:[a,b]\to\mathbb R} \displaystyle{f:[a,b]\to\mathbb R}](/forum/ext/geomar/texintegr/latexrender/pictures/80013b5c42fd16b152aa54b27273b1e7.png)
συνεχής μη αρνητική και γνησίως αύξουσα. Τότε για κάθε

θα ισχύει

για κάποιο
![x_{p}\in[a,b] x_{p}\in[a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/7da33e20790a7de47107e0a672894a45.png)
. Βρείτε το

.

Ας δειχθεί ότι το

όπου οι διαδοχικοί παρονομαστές ικανοποιούν την σχέση

είναι αμιγώς φανταστικός.

Ξέρουν και οι πέτρες ότι

. Αναζητούμε το

στη μορφή
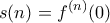
για κάποια
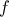
. Βρείτε μια έκφραση για την
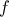
συναρτήσει του ολοκληρώματος μιας στοιχειώδους συνάρτησης. (

ο

οστός αρμονικός αριθμός)
Λύση της 5). Θα δούμε ότι

. Πράγματι:
Έστω

τυχαίο. Από το γεγονός ότι η
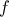
είναι μη αρνητική και γνησίως αύξουσα έχουμε

Άρα
![\displaystyle{ f(x_p) \ge \sqrt [p] {\frac{b-c}{b-a}} f(c)\,(*)} \displaystyle{ f(x_p) \ge \sqrt [p] {\frac{b-c}{b-a}} f(c)\,(*)}](/forum/ext/geomar/texintegr/latexrender/pictures/b8535b7a17ffdb8801f1c60966455ba2.png)
. Αλλά για κάθε σταθερά

είναι
![\displaystyle{\lim_{p\to +\infty} \sqrt [p]d=1} \displaystyle{\lim_{p\to +\infty} \sqrt [p]d=1}](/forum/ext/geomar/texintegr/latexrender/pictures/4b5c16ba92cb6cb14360fb67eece695f.png)
οπότε η

δίνει

Αφού
![x_p \in [a, \, b] x_p \in [a, \, b]](/forum/ext/geomar/texintegr/latexrender/pictures/c1cee985c44256a69fec77a13db11706.png)
και
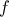
αύξουσα έχουμε

. Σε συνδυασμό με την προηγούμενη έχουμε

.
Και επειδή αυτό ισχύει για κάθε

, έπεται από την συνέχεια και την μονοτονία της
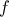
ότι

, που σημαίνει ότι έχουμε ισότητα παντού. Ειδικά το όριο

υπάρχει και είναι

.
Τώρα ουσιαστικά τελιώσαμε γιατί από την συνέχεια της

έχουμε

.
Φιλικά,
Μιχάλης

 ισχύει
ισχύει  . (Μια απόδειξη πχ εδώ, ή στο Νεγρεπόντη αν θυμάμαι καλά ή σε διάφορα άλλα βιβλία)
. (Μια απόδειξη πχ εδώ, ή στο Νεγρεπόντη αν θυμάμαι καλά ή σε διάφορα άλλα βιβλία) .
. επεκτείνεται περιοδικά σε όλο το
επεκτείνεται περιοδικά σε όλο το  με περίοδο
με περίοδο  , άρα η
, άρα η  επεκτείνεται περιοδικά στο
επεκτείνεται περιοδικά στο  με περίοδο
με περίοδο  και επιπλέον, αν
και επιπλέον, αν  και
και  , ισχύει ότι
, ισχύει ότι  για
για  με
με  .
.
 Χρωστάω τη δικαιολόγοση της εναλλαγής αθροίσματος - ολοκληρώματος η οποία θέλει το κατιτίς της.
Χρωστάω τη δικαιολόγοση της εναλλαγής αθροίσματος - ολοκληρώματος η οποία θέλει το κατιτίς της.

 Πόσο να κάνει τούτο δω...;
Πόσο να κάνει τούτο δω...; 
 .
. οποτε παραγωγίζοντας ως προς
οποτε παραγωγίζοντας ως προς  παίρνουμε ότι
παίρνουμε ότι 
 και παίρνουμε ότι:
και παίρνουμε ότι:
 .
. .
. είναι η συνάρτηση
είναι η συνάρτηση  . Περισσότερες πληροφορίες
. Περισσότερες πληροφορίες 
 Αθροισθήτω:
Αθροισθήτω:  , όπου
, όπου  .
. Έστω
Έστω ![\displaystyle{f:[a,b]\to\mathbb R} \displaystyle{f:[a,b]\to\mathbb R}](/forum/ext/geomar/texintegr/latexrender/pictures/80013b5c42fd16b152aa54b27273b1e7.png) συνεχής μη αρνητική και γνησίως αύξουσα. Τότε για κάθε
συνεχής μη αρνητική και γνησίως αύξουσα. Τότε για κάθε  θα ισχύει
θα ισχύει  για κάποιο
για κάποιο ![x_{p}\in[a,b] x_{p}\in[a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/7da33e20790a7de47107e0a672894a45.png) . Βρείτε το
. Βρείτε το  .
. Ας δειχθεί ότι το
Ας δειχθεί ότι το  όπου οι διαδοχικοί παρονομαστές ικανοποιούν την σχέση
όπου οι διαδοχικοί παρονομαστές ικανοποιούν την σχέση  είναι αμιγώς φανταστικός.
είναι αμιγώς φανταστικός. Ξέρουν και οι πέτρες ότι
Ξέρουν και οι πέτρες ότι  . Αναζητούμε το
. Αναζητούμε το  στη μορφή
στη μορφή 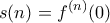 για κάποια
για κάποια 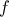 . Βρείτε μια έκφραση για την
. Βρείτε μια έκφραση για την  ο
ο  οστός αρμονικός αριθμός)
οστός αρμονικός αριθμός)
 . Πράγματι:
. Πράγματι: τυχαίο. Από το γεγονός ότι η
τυχαίο. Από το γεγονός ότι η 
![\displaystyle{ f(x_p) \ge \sqrt [p] {\frac{b-c}{b-a}} f(c)\,(*)} \displaystyle{ f(x_p) \ge \sqrt [p] {\frac{b-c}{b-a}} f(c)\,(*)}](/forum/ext/geomar/texintegr/latexrender/pictures/b8535b7a17ffdb8801f1c60966455ba2.png) . Αλλά για κάθε σταθερά
. Αλλά για κάθε σταθερά  είναι
είναι ![\displaystyle{\lim_{p\to +\infty} \sqrt [p]d=1} \displaystyle{\lim_{p\to +\infty} \sqrt [p]d=1}](/forum/ext/geomar/texintegr/latexrender/pictures/4b5c16ba92cb6cb14360fb67eece695f.png) οπότε η
οπότε η 
![x_p \in [a, \, b] x_p \in [a, \, b]](/forum/ext/geomar/texintegr/latexrender/pictures/c1cee985c44256a69fec77a13db11706.png) και
και  . Σε συνδυασμό με την προηγούμενη έχουμε
. Σε συνδυασμό με την προηγούμενη έχουμε .
. , έπεται από την συνέχεια και την μονοτονία της
, έπεται από την συνέχεια και την μονοτονία της  , που σημαίνει ότι έχουμε ισότητα παντού. Ειδικά το όριο
, που σημαίνει ότι έχουμε ισότητα παντού. Ειδικά το όριο  υπάρχει και είναι
υπάρχει και είναι  .
.  έχουμε
έχουμε .
. , οπότε δοκιμάζουμε τα
, οπότε δοκιμάζουμε τα  στην θέση των ζητούμενων
στην θέση των ζητούμενων  . Η ιδέα είναι να γράψουμε το προκύπτον άθροισμα σε κλειστή μορφή. Επιτρέποντας την εναλλαγή της σειράς ολοκλήρωσης έχουμε
. Η ιδέα είναι να γράψουμε το προκύπτον άθροισμα σε κλειστή μορφή. Επιτρέποντας την εναλλαγή της σειράς ολοκλήρωσης έχουμε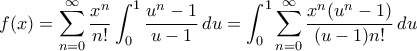
 , το προηγούμενο γίνεται
, το προηγούμενο γίνεται  .
.  και
και  ας κάνουμε την αλλαγή μεταβλητής
ας κάνουμε την αλλαγή μεταβλητής  οπότε
οπότε
![\displaystyle{\begin{aligned}
\sum_{n=1}^{\infty} \frac{1}{n} \int_{2\pi n}^{\infty} \frac{\sin z}{z} \, {\rm d}z &= \sum_{n=1}^{\infty} \frac{1}{n} \int_{0}^{\infty} \frac{\sin nt}{t+2\pi} \, {\rm d}t \\
&=\sum_{n=1}^{\infty} \sum_{m=1}^{\infty} \frac{1}{n} \int_{0}^{2\pi} \frac{\sin nt}{t + 2 m \pi} \, {\rm d}t \\
&= \sum_{m=1}^{\infty} \int_{0}^{2\pi} \sum_{n=1}^{\infty} \frac{1}{n} \frac{\sin nt}{t+ 2 m \pi} \, {\rm d}t \\
&= \sum_{m=1}^{\infty} \int_{0}^{2\pi} \frac{\pi -t}{2\left (t + 2 m\pi \right )} \, {\rm d}t\\
&= \pi \sum_{n=1}^{\infty} \left [ \left ( 1 + \frac{1}{2} \right ) \log \left ( 1 + \frac{1}{n} \right ) -1 \right ] \\
&=\pi \log \left [ \lim_{N \rightarrow +\infty} e^{-N} \prod_{n=1}^{N} \left ( \frac{n+1}{n} \right )^{n+1/2} \right ] \\
&= \pi \log \left ( \lim_{N \rightarrow +\infty} \frac{\sqrt{N+1}\left ( N+1 \right )^N e^{-N}}{N!} \right ) \\
&= \pi \log \left ( \frac{e}{\sqrt{2\pi}} \right ) \\
&= \pi - \frac{ \pi \log 2\pi}{2}
\end{aligned}} \displaystyle{\begin{aligned}
\sum_{n=1}^{\infty} \frac{1}{n} \int_{2\pi n}^{\infty} \frac{\sin z}{z} \, {\rm d}z &= \sum_{n=1}^{\infty} \frac{1}{n} \int_{0}^{\infty} \frac{\sin nt}{t+2\pi} \, {\rm d}t \\
&=\sum_{n=1}^{\infty} \sum_{m=1}^{\infty} \frac{1}{n} \int_{0}^{2\pi} \frac{\sin nt}{t + 2 m \pi} \, {\rm d}t \\
&= \sum_{m=1}^{\infty} \int_{0}^{2\pi} \sum_{n=1}^{\infty} \frac{1}{n} \frac{\sin nt}{t+ 2 m \pi} \, {\rm d}t \\
&= \sum_{m=1}^{\infty} \int_{0}^{2\pi} \frac{\pi -t}{2\left (t + 2 m\pi \right )} \, {\rm d}t\\
&= \pi \sum_{n=1}^{\infty} \left [ \left ( 1 + \frac{1}{2} \right ) \log \left ( 1 + \frac{1}{n} \right ) -1 \right ] \\
&=\pi \log \left [ \lim_{N \rightarrow +\infty} e^{-N} \prod_{n=1}^{N} \left ( \frac{n+1}{n} \right )^{n+1/2} \right ] \\
&= \pi \log \left ( \lim_{N \rightarrow +\infty} \frac{\sqrt{N+1}\left ( N+1 \right )^N e^{-N}}{N!} \right ) \\
&= \pi \log \left ( \frac{e}{\sqrt{2\pi}} \right ) \\
&= \pi - \frac{ \pi \log 2\pi}{2}
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/1c602f7fb671bd05a005f2a965ff9998.png)
 είναι
είναι  ( σειρά Fourier ) .
( σειρά Fourier ) . , όμως δεν έχω απόδειξη γι’ αυτό, ούτε μπόρεσα να ανακαλύψω κάποια.
, όμως δεν έχω απόδειξη γι’ αυτό, ούτε μπόρεσα να ανακαλύψω κάποια.

 η συνάρτηση ζήτα του Riemann και
η συνάρτηση ζήτα του Riemann και  η συνάρτηση του βήτα του Dirichlet. Υπάρχει αναλυτική λύση με μετασχηματισμούς Mellin καθώς επίσης και η φυσιολογική λύση η οποία χρησιμοποιεί το γεγονός ότι ο τρόπος να γραφεί ένας ακέραιος ως άθροισμα δύο ακεραίων είναι
η συνάρτηση του βήτα του Dirichlet. Υπάρχει αναλυτική λύση με μετασχηματισμούς Mellin καθώς επίσης και η φυσιολογική λύση η οποία χρησιμοποιεί το γεγονός ότι ο τρόπος να γραφεί ένας ακέραιος ως άθροισμα δύο ακεραίων είναι
