Πρόβλημα 1
Να βρεθούν όλα τα πολυώνυμα
 και οι μη σταθερές συναρτήσεις
και οι μη σταθερές συναρτήσεις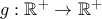 που ικανοποιούν την σχέχη:
που ικανοποιούν την σχέχη: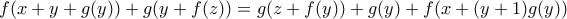 για κάθε θετικούς πραγματικούς
για κάθε θετικούς πραγματικούς 
Πρόβλημα 2
Δίνεται οξυγώνιο τρίγωνο
 με
με  εγγεγραμμένο σε κύκλο
εγγεγραμμένο σε κύκλο  καθώς και τα ύψη
καθώς και τα ύψητου
 τα οποία συντρέχουν στο ορθόκεντρο
τα οποία συντρέχουν στο ορθόκεντρο  . Οι εφαπτόμενες του
. Οι εφαπτόμενες του  στα σημεία
στα σημεία 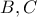
τέμνονται στο
 . Η
. Η  τέμνει την
τέμνει την  στο
στο  και η
και η  την
την  στο
στο  . Αν οι περιγεγραμμένοι
. Αν οι περιγεγραμμένοικύκλοι των τριγώνων
 και
και  τέμνουν τις
τέμνουν τις  αντιστοίχως στα σημεία
αντιστοίχως στα σημεία  , να αποδείξετε
, να αποδείξετεότι τα
 είναι ομοκυκλικά.
είναι ομοκυκλικά.Πρόβλημα 3
Να βρεθούν όλες οι τριάδες ακεραίων
 που ικανοποιούν την εξίσωση:
που ικανοποιούν την εξίσωση: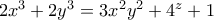
Πρόβλημα 4
Ο μικρός Θανάσης μαζί με τον Νίκο παίζουν το εξής παιχνίδι.
Αρχικά ο Θανάσης επιλέγει έναν θετικό ακέραιο
 με
με  και γράφει
και γράφει  θετικούς ακεραίους
θετικούς ακεραίουςσε έναν πίνακα έτσι ώστε ανά δύο να είναι διαφορετικοί μεταξύ τους. Στην συνέχεια, καλείται ο Νίκος να
σκεφτεί έναν θετικό ακέραιο από αυτούς που είναι γραμμένοι στον πίνακα. Ο σκοπός του παιχνιδιού, είναι
ο Θανάσης να βρει τον αριθμό που επέλεξε ο Νίκος μέσω ερωτήσεων. Σε κάθε κίνηση, ο Θανάσης μπορεί
να επιλέξει έναν οποιονδήποτε θετικό ακέραιο θελήσει (δεν χρειάζεται να υπάρχει κατ'ανάγκην στον πίνακα),
και να ρωτήσει τον Νίκο αν ο μέγιστος κοινός
διαιρέτης του αριθμού που επέλεξε ο Θανάσης με του Νίκου (δηλαδή αυτόν που είχε σκεφτεί) ισούται με
 .
.Ο Νίκος μπορεί να απαντήσει με "ναι" ή "όχι". Αν γνωρίζουμε ότι σε έναν γύρο:
(1) Ο Θανάσης επέλεξε
 σε πλήθος διαφορετικούς θετικούς ακεραίους (όχι αυτούς που έγραψε αρχικά στον πίνακα, αλλά αυτούς που επέλεγε
σε πλήθος διαφορετικούς θετικούς ακεραίους (όχι αυτούς που έγραψε αρχικά στον πίνακα, αλλά αυτούς που επέλεγεσε κάθε κίνηση), και εγγυήθηκε ότι ήταν αρκετοί για να προσδιορίσει με σιγουριά τον αριθμό του Νίκου μετά από μερικές κινήσεις.
(2) Για αυτά τα
 που διάλεξε, το κλάσμα
που διάλεξε, το κλάσμα  δέχθηκε την μεγαλύτερη τιμή που θα μπορούσε να πάρει.
δέχθηκε την μεγαλύτερη τιμή που θα μπορούσε να πάρει.(3) Έγραψε θετικούς ακεραίους αρχικά στον πίνακα, έτσι ώστε το άθροισμά τους να είναι το μικρότερο δυνατό για αυτά τα
 .
.Να βρεθούν οι αριθμοί
 καθώς και οι αριθμοί που έγραψε αρχικά στον πίνακα.
καθώς και οι αριθμοί που έγραψε αρχικά στον πίνακα.
 που εξασφαλίζουν στον Θανάση την νίκη. Για παράδειγμα αν παίρναμε
που εξασφαλίζουν στον Θανάση την νίκη. Για παράδειγμα αν παίρναμε 
 δεν μπορούμε να γράψουμε κατάλληλους θετικούς ακέραιους στον πίνακα, αλλά ούτε και να επιλέξουμε έτσι
δεν μπορούμε να γράψουμε κατάλληλους θετικούς ακέραιους στον πίνακα, αλλά ούτε και να επιλέξουμε έτσι είναι τα μέσα των αντίστοιχων πλευρών στα οποία βρίσκονται.
είναι τα μέσα των αντίστοιχων πλευρών στα οποία βρίσκονται. είναι εγγράψιμο στον κύκλο
είναι εγγράψιμο στον κύκλο  .
.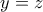 παίρνουμε
παίρνουμε  (1) Τώρα θέτοντας
(1) Τώρα θέτοντας  και θεωρώντας σταθερό το
και θεωρώντας σταθερό το  παίρνουμε:
παίρνουμε:
 είναι είτε σταθερό είτε γραμμικό.
είναι είτε σταθερό είτε γραμμικό.
 τότε η (1) γίνεται
τότε η (1) γίνεται 
 από όπου παίρνουμε πως (*)
από όπου παίρνουμε πως (*)  ή
ή 
 και
και  ή
ή  και
και 
 δεν μπορεί να είναι σταθερή από την εκφώνηση.
δεν μπορεί να είναι σταθερή από την εκφώνηση. .
. .
. .
. .
. , οπότε αφού
, οπότε αφού 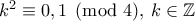 , είναι
, είναι  , άρα
, άρα 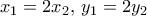 , οπότε με αντικατάσταση
, οπότε με αντικατάσταση  , άρα
, άρα  , και η διαδικασία επαναλαμβάνεται.
, και η διαδικασία επαναλαμβάνεται. στο δεξί μέλος είναι
στο δεξί μέλος είναι  , οπότε
, οπότε  , και το
, και το  φορές (μέχρι η δύναμη να είναι
φορές (μέχρι η δύναμη να είναι  )
) , και όμοια
, και όμοια  .
. .
. , άρα
, άρα  , άτοπο, αφού
, άτοπο, αφού 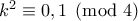 ,
,  , οπότε
, οπότε  .
. , δηλαδή
, δηλαδή  .
. ,
,  . Άρα, τα ζεύγη
. Άρα, τα ζεύγη  είναι λύσεις.
είναι λύσεις. .
. ή
ή 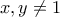 .
. . Απευθείας ελέγχουμε πως δεν γίνεται
. Απευθείας ελέγχουμε πως δεν γίνεται  , άρα
, άρα  .
. , και αφού
, και αφού  .
. .
. (1).
(1). , με
, με  , άρα η
, άρα η  , οπότε δεν υπάρχουν λύσεις.
, οπότε δεν υπάρχουν λύσεις. , θέτουμε
, θέτουμε  , και εφαρμόζουμε την ίδια διαδικασία, θεωρώντας την συνάρτηση
, και εφαρμόζουμε την ίδια διαδικασία, θεωρώντας την συνάρτηση  .
. .
. .
. τότε
τότε  άρα
άρα  .
. τέτοιος ώστε:
τέτοιος ώστε:  που είναι το άθροισμα 2 τετραγώνων άρα
που είναι το άθροισμα 2 τετραγώνων άρα 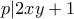 και
και 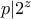 , άρα
, άρα  που είναι άτοπο, επομένως
που είναι άτοπο, επομένως 



 έχουμε:
έχουμε: (1)
(1)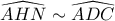
 κοινή γωνία,ορθογώνια )
κοινή γωνία,ορθογώνια )
 :
:
 :
:
 (από την σχεση 1)
(από την σχεση 1)


 ως εντός εναλλάξ των παράλληλων HN και BC(2)
ως εντός εναλλάξ των παράλληλων HN και BC(2) ισοσκελες(AN=ND)
ισοσκελες(AN=ND)
 (
( ,ορθ τρίγωνα)
,ορθ τρίγωνα) θα είναι όμοιο και με το ορθ ισοσκελες
θα είναι όμοιο και με το ορθ ισοσκελες  μέσον AC
μέσον AC , οπότε το
, οπότε το  είναι το μέσο της
είναι το μέσο της  και όμοια το
και όμοια το  της
της  , άρα τα
, άρα τα  , δηλαδή είναι ομοκυκλικά.
, δηλαδή είναι ομοκυκλικά. .
. , τότε τα
, τότε τα  είναι συνευθειακά.
είναι συνευθειακά. και
και 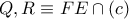 .
. ανήκει στην πολική του
ανήκει στην πολική του 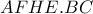 παίρνουμε ότι τα
παίρνουμε ότι τα  είναι αρμονικά συζυγή, οπότε το
είναι αρμονικά συζυγή, οπότε το  ανήκει στην πολική του
ανήκει στην πολική του  (με το
(με το  σε διαφορετικό ημιεπίπεδο της
σε διαφορετικό ημιεπίπεδο της  ).
).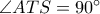 και το
και το  , το
, το  ανήκει στον κύκλο
ανήκει στον κύκλο 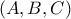 .
. και
και  , άρα η
, άρα η  είναι μεσοκάθετος της
είναι μεσοκάθετος της  , άρα
, άρα  , οπότε
, οπότε  .
. , συνεπώς τα
, συνεπώς τα  είναι αρμονικά συζυγή, που σημαίνει ότι το
είναι αρμονικά συζυγή, που σημαίνει ότι το  περνά από το μέσο της
περνά από το μέσο της  , και όμοια
, και όμοια  , άρα το
, άρα το  είναι παραλληλόγραμμο, άρα η
είναι παραλληλόγραμμο, άρα η