Άσκηση 1 Έστω ή δύο φορές παραγωγίσιμη συνάρτηση
 . Αν η
. Αν η  είναι γνησίως αύξουσα και κυρτή, τότε να αποδείξετε ότι υπάρχει μοναδικό
είναι γνησίως αύξουσα και κυρτή, τότε να αποδείξετε ότι υπάρχει μοναδικό 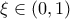 τέτοιο, ώστε:
τέτοιο, ώστε:
 Άσκηση 2 Να αποδείξετε ότι η εξίσωση
Άσκηση 2 Να αποδείξετε ότι η εξίσωση  έχει ακριβώς μία ρίζα στο διάστημα
έχει ακριβώς μία ρίζα στο διάστημα  .
.Μέχρι 12/12/2016.
Φιλικά,
Μάριος
*Προστέθηκε ερώτημα (1:21 π.μ.)

![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png)
 .
.
 , αφού
, αφού 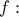 γνησίως αύξουσα.
γνησίως αύξουσα.
![[1,2] [1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/f79408e5ca998cd53faf44af31e6eb45.png) , αντιστοίχως προκύπτει:
, αντιστοίχως προκύπτει: και
και  με
με 
 διότι η
διότι η  είναι γνησίως αύξουσα επειδή η
είναι γνησίως αύξουσα επειδή η  στο
στο  ,
, , διότι η
, διότι η  γνησίως αύξουσα , συνεπώς το
γνησίως αύξουσα , συνεπώς το  : μοναδικό.
: μοναδικό.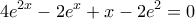 .
. με τύπο
με τύπο  , η οποία είναι παραγωγίσιμη στο
, η οποία είναι παραγωγίσιμη στο  με
με  για κάθε
για κάθε  (καθώς η διακρίνουσα του τριωνύμου είναι αρνητική).
(καθώς η διακρίνουσα του τριωνύμου είναι αρνητική). και
και  .
. έχει μία τουλάχιστον ρίζα στο
έχει μία τουλάχιστον ρίζα στο  και επειδή η
και επειδή η