Βρείτε όλες τις ακέραιες λύσεις της εξίσωσης:

Σκέφτηκα τα εξής:
Από το θεώρημα του Fermat:
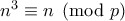


Οπότε η εξίσωση ισχύει
 .
.Ήθελα να το επαληθεύσω,επιλέγοντας το
 .
.Σε αυτή την περίπτωση ,
 .
.Έχω κάνει κάποιο λάθος;
Συντονιστής: nkatsipis

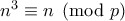


 .
. .
. .
. το προσπερνώ ως τυπογραφικό.
το προσπερνώ ως τυπογραφικό. ισχύει για κάθε
ισχύει για κάθε  .
. .
.Δηλαδή δεν ισχύειΑρχιμήδης 6 έγραψε:Καλησπέρα.
Σοβαρά σφάλματα ως προς τον τρόπο λογικής που έχεις.
Καταρχήν τοτο προσπερνώ ως τυπογραφικό.
Στο σημείο που συμπεραίνεις ότι
ισχύει για κάθε
.
Άρα και η εξίσωση είναι αληθής για κάθε.
Εδώ υπάρχει λάθος .
 ;
;  την επαληθεύει.
την επαληθεύει.
 μηδενίζει και προκύπτει η λύση
μηδενίζει και προκύπτει η λύση 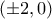
 τότε
τότε  περιττός τότε
περιττός τότε 
 ώστε
ώστε 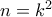 ,
, η
η ,
, 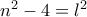
 άρα
άρα  (την έχω ήδη)
(την έχω ήδη)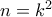 ,
,  ,
,  περιττός.
περιττός.
 άρα
άρα  αδύνατον .
αδύνατον . περιττό δεν έχω λύση.
περιττό δεν έχω λύση. άρτιο άλλη στιγμή γιατί είναι αρκετές υποπεριπτώσεις .
άρτιο άλλη στιγμή γιατί είναι αρκετές υποπεριπτώσεις .Συνεχίζω από εκεί που σταμάτησα....Αρχιμήδης 6 έγραψε:
Ανμηδενίζει και προκύπτει η λύση
Αντότε
Ανπεριττός τότε
Άρα υπάρχουν ακέραιοιώστε
,
η
,
Το δεύτερο σύστημα μας δίνει προφανώς μόνο την λύσηάρα
(την έχω ήδη)
Για το πρώτο σύστημα...
,
,
περιττός.

άρα
αδύνατον .
Αποδείξαμε ότι γιαπεριττό δεν έχω λύση.
Γιαάρτιο άλλη στιγμή γιατί είναι αρκετές υποπεριπτώσεις .
 άρτιος
άρτιος


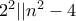
 άρα
άρα ,
,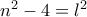 η
η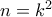 ,
,
 ,
,
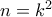 ,
, 
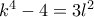
 περιττός τότε
περιττός τότε 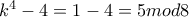 , άρα
, άρα  Αδύνατον.
Αδύνατον. άρτιος τότε
άρτιος τότε  ,
,  οπότε
οπότε


 δεν είναι ποτέ πολλαπλάσιο του
δεν είναι ποτέ πολλαπλάσιο του  οπότε
οπότε  ,
,  άρα υπάρχουν ακέραιοι ώστε
άρα υπάρχουν ακέραιοι ώστε ,
, 
 περιττοί
περιττοί

 περιττός
περιττός ,
,
 ,
,  με
με  . άρα
. άρα 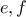 περιττοί
περιττοί η
η  και αφού
και αφού 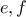 περιττοί τότε
περιττοί τότε 
 που έχουμε συναρτήσει των
που έχουμε συναρτήσει των 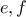 στην
στην  θα καταλήξουμε σε εξίσωση της μορφής
θα καταλήξουμε σε εξίσωση της μορφής  ,
,  άρα
άρα  ,
,  . ( ****edit τυπογραφικό)
. ( ****edit τυπογραφικό) ,
,  κάνοντας το ίδιο θα καταλήξω στην
κάνοντας το ίδιο θα καταλήξω στην  με λύση την
με λύση την 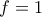 που βλέπω ότι δεν έχει λύση στην αρχική.
που βλέπω ότι δεν έχει λύση στην αρχική. Μοναδική λύση
Μοναδική λύση 

Αρχιμήδης 6 έγραψε:Συνεχίζω από εκεί που σταμάτησα....Αρχιμήδης 6 έγραψε:
Ανμηδενίζει και προκύπτει η λύση
Αντότε
Ανπεριττός τότε
Άρα υπάρχουν ακέραιοιώστε
,
η
,
Το δεύτερο σύστημα μας δίνει προφανώς μόνο την λύσηάρα
(την έχω ήδη)
Για το πρώτο σύστημα...
,
,
περιττός.

άρα
αδύνατον .
Αποδείξαμε ότι γιαπεριττό δεν έχω λύση.
Γιαάρτιο άλλη στιγμή γιατί είναι αρκετές υποπεριπτώσεις .
Ανάρτιος
Βλέπω ότι τότε
Για την περίπτωση που
Εδώ είναι εμφανές ότι
Σε αυτή την περίπτωση θα ισχύει ότι
άρα
έχω 2 περιπτώσεις.
,
η
,

Για την πρώτη περίπτωση είναι εύκολο να διαπιστώσω ότι μοναδική λύση είναι,

Για την δεύτερη περίπτωση..,

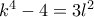
Ανπεριττός τότε
, άρα
Αδύνατον.
Ανάρτιος τότε
,
οπότε
Η παράστασηδεν είναι ποτέ πολλαπλάσιο του
οπότε
,
άρα υπάρχουν ακέραιοι ώστε
,

περιττοί
Αθροίζοντας θα έχω

περιττός
,

η,
με
. άρα
περιττοί
Σε κάθε περίπτωσηη
και αφού
περιττοί τότε
Σε κάθε περίπτωση αν αντικαταστήσουμε τοπου έχουμε συναρτήσει των
στην
θα καταλήξουμε σε εξίσωση της μορφής
,
άρα
,
. ( ****edit τυπογραφικό)
Για την περίπτωση που,
κάνοντας το ίδιο θα καταλήξω στην
με λύση την
που βλέπω ότι δεν έχει λύση στην αρχική.
Απέδειξα ότι ανΜοναδική λύση
Υπόψιν μένει η περίπτωση που
 ,
,  .
. της
της 
 θεωρώ ότι υπάρχει θετικός
θεωρώ ότι υπάρχει θετικός  ώστε
ώστε  .
.
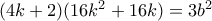
 (Εδώ
(Εδώ  και θέτω
και θέτω  )
)



 ,
,  ,
, .
. προκύπτει από μια τετριμμένη λύση μιας άλλης διοφαντικής της μορφής
προκύπτει από μια τετριμμένη λύση μιας άλλης διοφαντικής της μορφής 
Αυτή είναι η δυσκολότερη περίπτωση του προβλήματος και η τελευταία εξίσωση είναι αρκετά γνωστή στη βιβλιογραφία αφού δυσκόλεψε αρκετά και υπάρχουν μόνοΑρχιμήδης 6 έγραψε:
Για την περίπτωση πουθεωρώ ότι υπάρχει θετικός
ώστε
.
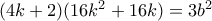
(Εδώ
και θέτω
)
Στην περίπτωση μας οι λύσεις της εξίσωσης ισοδυναμούν με τις λύσεις της παρακάτω εξίσωσης

που παρουσιάζει αρκετό ενδιαφέρον γιατί δεν την είχα ξανασυναντήσει ...
 στοιχειώδη αποδείξεις και κάποιες άλλες μη (για τη μια είμαι σίγουρος του Anglin που έχω διαβάσει)
στοιχειώδη αποδείξεις και κάποιες άλλες μη (για τη μια είμαι σίγουρος του Anglin που έχω διαβάσει) παραπέμπω εδώ:
παραπέμπω εδώ:Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες