Δίνεται ημικύκλιο διαμέτρου
 και η εφαπτομένη του
και η εφαπτομένη του  στο
στο  .
.Ευθεία διερχόμενη από το
 τέμνει το ημικύκλιο στο
τέμνει το ημικύκλιο στο  και την
και την  στο
στο  .
.Αν
 , να υπολογίσετε το
, να υπολογίσετε το  .
.Συντονιστής: gbaloglou
 και η εφαπτομένη του
και η εφαπτομένη του  στο
στο  .
. τέμνει το ημικύκλιο στο
τέμνει το ημικύκλιο στο  και την
και την  στο
στο  .
. , να υπολογίσετε το
, να υπολογίσετε το  .
. είναι
είναι  (1).
(1).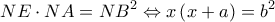
 , άρα η (1) γίνεται
, άρα η (1) γίνεται  (2).
(2).  , αφού η γωνία είναι οξεία, οπότε η (2) γίνεται
, αφού η γωνία είναι οξεία, οπότε η (2) γίνεται  .
.Με προλάβανε αλλά έχουμε και γιορτή!Φανης Θεοφανιδης έγραψε: ↑Σάβ Ιαν 06, 2018 6:56 pm1.png
Καλησπέρα και Χρόνια Πολλά.
Δίνεται ημικύκλιο διαμέτρουκαι η εφαπτομένη του
στο
.
Ευθεία διερχόμενη από τοτέμνει το ημικύκλιο στο
και την
στο
.
Αν, να υπολογίσετε το
.
 χωρίζει το
χωρίζει το  σε μέσο κι άκρο λόγο.
σε μέσο κι άκρο λόγο. .
. και
και  τα ορθογώνια τρίγωνα
τα ορθογώνια τρίγωνα 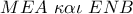 είναι ίσα και άρα
είναι ίσα και άρα  .
.
Για να πω ξανά τα Χρόνια Πολλά στο Φάνη!Φανης Θεοφανιδης έγραψε: ↑Σάβ Ιαν 06, 2018 6:56 pm1.png
Καλησπέρα και Χρόνια Πολλά.
Δίνεται ημικύκλιο διαμέτρουκαι η εφαπτομένη του
στο
.
Ευθεία διερχόμενη από τοτέμνει το ημικύκλιο στο
και την
στο
.
Αν, να υπολογίσετε το
.
 είναι ίσα.
είναι ίσα.
Φανης Θεοφανιδης έγραψε: ↑Σάβ Ιαν 06, 2018 6:56 pm1.png
Καλησπέρα και Χρόνια Πολλά.
Δίνεται ημικύκλιο διαμέτρουκαι η εφαπτομένη του
στο
.
Ευθεία διερχόμενη από τοτέμνει το ημικύκλιο στο
και την
στο
.
Αν, να υπολογίσετε το
.
 και
και 

 .Άρα
.Άρα 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες