Δίνεται τεταρτοκύκλιο
 και το ημικύκλιο διαμέτρου
και το ημικύκλιο διαμέτρου  ,
,στο εσωτερικό του τεταρτοκυκλίου, το οποίο τέμνει την
 στο
στο  .
.Αν
 , να υπολογίσετε την
, να υπολογίσετε την  .
.Συντονιστής: gbaloglou
 και το ημικύκλιο διαμέτρου
και το ημικύκλιο διαμέτρου  ,
, στο
στο  .
. , να υπολογίσετε την
, να υπολογίσετε την  .
. . Το κέντρο του ημικυκλίου έστω
. Το κέντρο του ημικυκλίου έστω  και η
και η  τέμνει την
τέμνει την  στο
στο  .
. τα ισοσκελή τρίγωνα
τα ισοσκελή τρίγωνα  είναι ισογώνια και έτσι
είναι ισογώνια και έτσι  που μας εξασφαλίζει ότι το τετράπλευρο
που μας εξασφαλίζει ότι το τετράπλευρο  είναι εγγράψιμο .
είναι εγγράψιμο .

Καλησπέρα! Από το σύστημαΦανης Θεοφανιδης έγραψε: ↑Τετ Δεκ 27, 2017 7:13 pm
Καλησπέρα.
Δίνεται τεταρτοκύκλιοκαι το ημικύκλιο διαμέτρου
,
στο εσωτερικό του τεταρτοκυκλίου, το οποίο τέμνει τηνστο
.
Αν, να υπολογίσετε την
.
 καταλήγουμε στο τριώνυμο ως προς
καταλήγουμε στο τριώνυμο ως προς  με δεκτή λύση
με δεκτή λύση 

 είναι ισοσκελές και το
είναι ισοσκελές και το  είναι ύψος στην
είναι ύψος στην  άρα είναι και διάμεσος.
άρα είναι και διάμεσος. 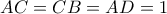 .
. ώσπου τέμνει τον κύκλο που έχει διάμετρο
ώσπου τέμνει τον κύκλο που έχει διάμετρο  στο
στο  .
. .
. ,
,  και
και  .
. .
.
 .
.

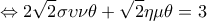 (1).
(1). . Θέτω
. Θέτω  , οπότε η (1) γίνεται
, οπότε η (1) γίνεται .
. άρα
άρα  , (που απλά σημαίνει ότι το
, (που απλά σημαίνει ότι το  ταυτίζεται με το
ταυτίζεται με το  ).
). .
. το κέντρο του ημικυκλίου. Προφανώς το
το κέντρο του ημικυκλίου. Προφανώς το  είναι μέσο
είναι μέσο .
. έπεται ότι η
έπεται ότι η  είναι μεσοκάθετος του
είναι μεσοκάθετος του  .
. και
και  .
. και
και  .
. έχω ότι
έχω ότι  .
. .
. μου δίνει ότι
μου δίνει ότι  .
. .
.
 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 14 επισκέπτες