Να υπολογίσετε το x

Barham76 · #1

Να υπολογίσετε το

$x^{12}=2^x$

Γιώργος Απόκης · #2

Επαναφέρω...

#3

Barham76 έγραψε:Να υπολογίσετε το
$x^{12}=2^x$

Η εξίσωση δεν βλέπω να έχει κάποιο ιδιαίτερο ενδιαφέρον όσον αφορά τις ρίζες της. Το Wolfram Alpha δίνει 12 λύσεις -''πρωταρχικές"- συναρτήσει της συνάρτησης LambertW, χωρίς να υπάρχει περαιτέρω δυνατότητα απλοποίησης των εκφράσεων. Υπάρχουν μιγαδικές, αλλά και οι πραγματικές ρίζες.

Γιώργος Απόκης · #4

Γρηγόρη καλημέρα κι ευχαριστώ για την απάντηση. Δε μπόρεσα να βγάλω άκρη, κι εγώ στο Wolfram κατέφυγα...

#5

Barham76 έγραψε:Να υπολογίσετε το
$x^{12}=2^x$

Δεν μπορώ να ανοίξω το λινκ του Γρηγόρη (μάλλον φταίει το δικό μου ιντερνέτ). Γράφω λύση εξ αρχής με φόβο μήπως επαναλάβω γεγραμμένα.

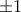Η εξίσωση έχει δύο πραγματικές λύσεις, μία θετική και μία αρνητική, κοντά στα $\pm 1$ και μία "μεγάλη", οι οποίες εκφράζονται με χρήση της (πλειότιμης) συνάρτησης W του Lambert (= η αντίστροφη της ze^z

).

Έχουμε $x^{12}=2^x$ οπότε για x>0

λαμβάνουμε

$\displaystyle{1=x2^{-\frac {x}{12}} = xe^{- \frac {x\ln 2}{12}}}$ άρα

$\displaystyle{- \frac {x\ln 2}{12}}e^{- \frac {x\ln 2}{12}}= - \frac {\ln 2}{12}}}$

Γράφοντας $y=- \frac {x\ln 2}{12}$ η προηγούμενη γίνεται $\displaystyle{ye^{y}= - \frac {\ln 2}{12}}}$

οπότε $\displaystyle{y= W \left ( - \frac {\ln 2}{12}\right ) }$ και τελικά

$\displaystyle{ \boxed {x=-\frac {12}{\ln 2} W \left ( - \frac {\ln 2}{12}\right ) }}$

Όμοια για την αρνητική ρίζα.

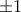Με κομπιουτεράκι βρήκα ότι οι δύο πραγματικές ρίζες που είναι κοντά στα $\pm 1$ είναι περίπου 1,063346

και

. H "μεγάλη" είναι μεταξύ

και

(δεν την υπολόγισα).

Σχόλιο: Ο λόγος που εμφανίζονται τρεις πραγματικές ρίζες αντί του "αναμενόμενου" δύο είναι γιατί η Lambert στο διάστημα $\displaystyle{ \left [ -\frac {1}{e}, \, 0 \right )}$ είναι δίτιμη, και το $\displaystyle{ - \frac {\ln 2}{12}\right \approx - 0,05776}$ πέφτει σε αυτό το διάστημα.

Να υπολογίσετε το x

Να υπολογίσετε το x

Re: Να υπολογίσετε το x

Re: Να υπολογίσετε το x

Re: Να υπολογίσετε το x

Re: Να υπολογίσετε το x

Μέλη σε σύνδεση