 με ακέραιους συντελεστές, αν
με ακέραιους συντελεστές, αν 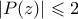 για κάθε μιγαδικό αριθμό
για κάθε μιγαδικό αριθμό  με
με  ;
;Συντονιστής: Demetres
 με ακέραιους συντελεστές, αν
με ακέραιους συντελεστές, αν 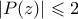 για κάθε μιγαδικό αριθμό
για κάθε μιγαδικό αριθμό  με
με  ;
; μη μηδενικούς συντελεστές (παράδειγμα
μη μηδενικούς συντελεστές (παράδειγμα 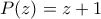 ). Θα αποδείξουμε ότι δεν μπορούμε να έχουμε περισσότερους. Θέτουμε
). Θα αποδείξουμε ότι δεν μπορούμε να έχουμε περισσότερους. Θέτουμε  .
.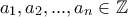 οι μη μηδενικοί συντελεστές. Τότε, ισχύει
οι μη μηδενικοί συντελεστές. Τότε, ισχύει όπου
όπου  ο βαθμός του όρου που αντιστοιχεί στον συντελεστή
ο βαθμός του όρου που αντιστοιχεί στον συντελεστή  .
. είναι
είναι 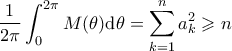 . Αφού
. Αφού 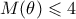 , η περίπτωση
, η περίπτωση  απορρίπτεται.
απορρίπτεται.  γιατί τότε το
γιατί τότε το  θα έπρεπε να είναι σταθερό (που δεν ισχύει, αφού απομένει τουλάχιστον ένας όρος συνημιτόνου, αυτός με την ελάχιστη περίοδο).
θα έπρεπε να είναι σταθερό (που δεν ισχύει, αφού απομένει τουλάχιστον ένας όρος συνημιτόνου, αυτός με την ελάχιστη περίοδο). . Πρέπει να ισχύει
. Πρέπει να ισχύει 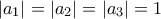 (αλλιώς η μέση τιμή υπερβαίνει πάλι το
(αλλιώς η μέση τιμή υπερβαίνει πάλι το  ), ενώ οι συντελεστές δεν μπορούν να είναι ομόσημοι (αλλιώς
), ενώ οι συντελεστές δεν μπορούν να είναι ομόσημοι (αλλιώς  ). Έστω
). Έστω 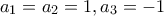 χωρίς βλάβη της γενικότητας. Έτσι
χωρίς βλάβη της γενικότητας. Έτσι
 δύο είναι ίσα και το τρίτο είναι μεγαλύτερο.
δύο είναι ίσα και το τρίτο είναι μεγαλύτερο. τότε
τότε  και ένα από τα δύο μέτρα υπερβαίνει το
και ένα από τα δύο μέτρα υπερβαίνει το  . Ομοίως αν
. Ομοίως αν  .
. , τότε
, τότε  .
.  .
. και η
και η  έχει
έχει  στην μοναδιαία περιφέρεια.
στην μοναδιαία περιφέρεια.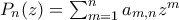 όπου
όπου 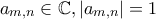

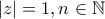 να ισχύει
να ισχύει 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες