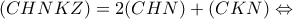Ένα σχολείο έχει
 μαθητές. Σε μια έρευνα που έγινε στο σχολείο διαπιστώθηκε ότι:
μαθητές. Σε μια έρευνα που έγινε στο σχολείο διαπιστώθηκε ότι:i. Οι
 μαθητές έχουν στην κατοχή τους ποδήλατο.
μαθητές έχουν στην κατοχή τους ποδήλατο.ii. Οι
 μαθητές έχουν κινητό τηλέφωνο.
μαθητές έχουν κινητό τηλέφωνο.iii. Οι
 μαθητές έχουν μπάλα ποδοσφαίρου.
μαθητές έχουν μπάλα ποδοσφαίρου. iv. Οι
 μαθητές έχουν ηλεκτρονικό υπολογιστή.
μαθητές έχουν ηλεκτρονικό υπολογιστή. Να βρείτε τον ελάχιστο αριθμό μαθητών που έχουν σίγουρα στην κατοχή τους και ποδήλατο και κινητό τηλέφωνο και μπάλα ποδοσφαίρου και ηλεκτρονικό υπολογιστή.
Πρόβλημα 2
Δίνεται ο αριθμός
 , με
, με  και
και  να είναι πρώτοι μεταξύ τους.
να είναι πρώτοι μεταξύ τους.Να προσδιορίσετε όλα τα ζεύγη
 , για τα οποία ο αριθμός
, για τα οποία ο αριθμός  είναι ακέραιος.
είναι ακέραιος.Πρόβλημα 3
Δίνεται ισοσκελές τρίγωνο

 . Φέρουμε τις διχοτόμους
. Φέρουμε τις διχοτόμους  των γωνιών
των γωνιών  , αντίστοιχα. Από την κορυφή
, αντίστοιχα. Από την κορυφή  φέρουμε τις κάθετες
φέρουμε τις κάθετες 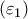 και
και 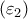 προς τις
προς τις  και
και  , οι οποίες τέμνουν τις διχοτόμους
, οι οποίες τέμνουν τις διχοτόμους  στα σημεία
στα σημεία  , αντίστοιχα. Έστω
, αντίστοιχα. Έστω  τα σημεία τομής των
τα σημεία τομής των 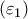 και
και 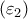 με την ευθεία
με την ευθεία  , αντίστοιχα. Αν
, αντίστοιχα. Αν  είναι τα μέσα των ευθύγραμμων τμημάτων
είναι τα μέσα των ευθύγραμμων τμημάτων  , αντίστοιχα, να αποδείξετε ότι:
, αντίστοιχα, να αποδείξετε ότι:(α) Το τετράπλευρο
 είναι ισοσκελές τραπέζιο.
είναι ισοσκελές τραπέζιο.(β)

Σημείωση: Με
 συμβολίζουμε τον εμβαδόν του σχήματος
συμβολίζουμε τον εμβαδόν του σχήματος  .
.Πρόβλημα 4
Δίνονται οι πραγματικοί αριθμοί
 τέτοιοι, ώστε
τέτοιοι, ώστε  . Να βρείτε όλες τις δυνατές τιμές του
. Να βρείτε όλες τις δυνατές τιμές του  .
.


 είναι ίσα διότι έχουν
είναι ίσα διότι έχουν  Άρα
Άρα 
 τα ορθογώνια τρίγωνα
τα ορθογώνια τρίγωνα  είναι ισογώνια, οπότε
είναι ισογώνια, οπότε  άρα
άρα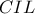 είναι ισοσκελές κι επειδή
είναι ισοσκελές κι επειδή  θα είναι
θα είναι  και το ζητούμενο έπεται.
και το ζητούμενο έπεται. οι προβολές των
οι προβολές των  στην
στην  Επειδή
Επειδή  είναι το μέσο της
είναι το μέσο της  θα είναι
θα είναι