Θέματα της φάσης επιλογής (*) για την 9η τάξη
1. Τετραγωνισμένο τετράγωνο
 διαμερίστηκε σε τετράγωνα
διαμερίστηκε σε τετράγωνα 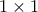 και
και  . Να αποδείξετε, ότι θα βρεθεί μια γραμμή του αρχικού τετραγώνου, που τέμνει περιττό αριθμό τετραγώνων της διαμέρισης. (Μπερλόβ)
. Να αποδείξετε, ότι θα βρεθεί μια γραμμή του αρχικού τετραγώνου, που τέμνει περιττό αριθμό τετραγώνων της διαμέρισης. (Μπερλόβ)2. Οι διαφορετικοί μεταξύ τους μη μηδενικοί φυσικοί αριθμοί
 και
και  ικανοποιούν την σχέση
ικανοποιούν την σχέση  . Να αποδείξετε, ότι
. Να αποδείξετε, ότι  . (Μπερλόβ)
. (Μπερλόβ)3. Ευθεία, διερχόμενη από το σημείο τομής των διαγώνιων τραπεζίου
 και παράλληλη προς τις βάσεις
και παράλληλη προς τις βάσεις  και
και  αυτού, τέμνει την πλευρά
αυτού, τέμνει την πλευρά  στο σημείο
στο σημείο  . Κύκλος διερχόμενος από τις κορυφές
. Κύκλος διερχόμενος από τις κορυφές  και
και  του τραπεζίου, τέμνει τις βάσεις του
του τραπεζίου, τέμνει τις βάσεις του  και
και  στα σημεία
στα σημεία  και
και  αντίστοιχα και εφάπτεται της πλευράς
αντίστοιχα και εφάπτεται της πλευράς  στο σημείο
στο σημείο  . Αποδείξτε, ότι η ευθεία
. Αποδείξτε, ότι η ευθεία  διέρχεται από το σημείο τομής των ευθείών
διέρχεται από το σημείο τομής των ευθείών  και
και  . (Μπερλόβ)
. (Μπερλόβ)4. Ο Λευτέρης έχει
 νομίσματα (
νομίσματα (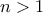 ), από τα οποία τα μισά και πάνω είναι γνήσια. Είναι γνωστό, ότι όλα τα γνήσια νομίσματα έχουν το ίδιο βάρος και το βάρος κάθε κάλπικου νομίσματος διαφέρει από το βάρος ενός αληθινού (όμως μπορεί διαφορετικά μεταξύ τους κάλπικα νομίσματα να έχουν διαφορετικό βάρος). Να αποδείξετε, ότι με
), από τα οποία τα μισά και πάνω είναι γνήσια. Είναι γνωστό, ότι όλα τα γνήσια νομίσματα έχουν το ίδιο βάρος και το βάρος κάθε κάλπικου νομίσματος διαφέρει από το βάρος ενός αληθινού (όμως μπορεί διαφορετικά μεταξύ τους κάλπικα νομίσματα να έχουν διαφορετικό βάρος). Να αποδείξετε, ότι με  ζυγίσεις σε ζυγό ισορροπίας χωρίς σταθμά ο Λευτέρης θα μπορέσει να βρει τουλάχιστόν ένα γνήσιο νόμισμα. (Κάρποβ, Πάστορ)
ζυγίσεις σε ζυγό ισορροπίας χωρίς σταθμά ο Λευτέρης θα μπορέσει να βρει τουλάχιστόν ένα γνήσιο νόμισμα. (Κάρποβ, Πάστορ)5. Στον πίνακα είναι γραμμένο το τριώνυμο
 . Παίζουν δυο: με μια κίνηση επιτρέπεται να αφαιρεθεί μια μονάδα είτε από τον συντελεστή του
. Παίζουν δυο: με μια κίνηση επιτρέπεται να αφαιρεθεί μια μονάδα είτε από τον συντελεστή του  , είτε από τον σταθερό συντελεστή. Κερδίζει αυτός, μετά την κίνηση του οποίου πρώτη φορά θα εμφανιστεί τριώνυμο, που έχει πραγματική ρίζα. Ποιος κερδίζει αν παίξει σωστά; (Ιβάνοβα)
, είτε από τον σταθερό συντελεστή. Κερδίζει αυτός, μετά την κίνηση του οποίου πρώτη φορά θα εμφανιστεί τριώνυμο, που έχει πραγματική ρίζα. Ποιος κερδίζει αν παίξει σωστά; (Ιβάνοβα) 6. Το
 είναι εγγεγραμμένο τετράπλευρο για το οποίο ισχύει
είναι εγγεγραμμένο τετράπλευρο για το οποίο ισχύει  . Το σημείο
. Το σημείο  είναι το μέσο της διαγωνίου
είναι το μέσο της διαγωνίου  . Να αποδείξετε, ότι
. Να αποδείξετε, ότι  . (Παστόρ)
. (Παστόρ)7. Θεωρούμε την τοποθέτηση
 των αριθμών
των αριθμών  και
και  πάνω σε κύκλο. Έστω
πάνω σε κύκλο. Έστω  , το πλήθος των αλλαγών προσήμου καθώς διατρέχουμε όλο τον κύκλο. Να βρείτε το άθροισμα των αριθμών
, το πλήθος των αλλαγών προσήμου καθώς διατρέχουμε όλο τον κύκλο. Να βρείτε το άθροισμα των αριθμών  για όλες τις δυνατές τοποθετήσεις. (Καρπόβ)
για όλες τις δυνατές τοποθετήσεις. (Καρπόβ)8. Να λύσετε στους μη μηδενικούς φυσικούς την εξίσωση
 . (Πετρόβ)
. (Πετρόβ)(*) Η φάση επιλογής διαξάγοταν μέχρι το 2008 και είχε ως σκοπό την επιλογή της ομάδας που θα εκπροσωπούσε την περιοχή της Αγιάς Πετρούπολης στην πανρωσική ολυμπιάδα. Από το 2009 και ύστερα αυτή η φάση είναι ενιαία για όλη την Ρωσία και είναι η τρίτη φάση της πανρωσικής ολυμπιάδας.

 , οπότε
, οπότε  περιττοί, οπότε
περιττοί, οπότε  , άτοπο.
, άτοπο. .
. , και αφού
, και αφού  .
.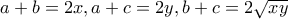 .
. .
. , και αν
, και αν  , είναι
, είναι  τέλειο τετράγωνο, και αφού
τέλειο τετράγωνο, και αφού  , είναι
, είναι  .
. , και άρα θέλουμε να δείξουμε ότι
, και άρα θέλουμε να δείξουμε ότι  , και αφού
, και αφού  , θέλουμε
, θέλουμε  .
. , και άρα αρκεί
, και άρα αρκεί ![(k^2-\ell^2)^2> \dfrac{(k+\ell)^2}{2} \Rightarrow [(k-\ell)(k+\ell)]^2>\dfrac{(k+\ell)^2}{2} \Rightarrow (k-\ell)^2>\dfrac{1}{2} (k^2-\ell^2)^2> \dfrac{(k+\ell)^2}{2} \Rightarrow [(k-\ell)(k+\ell)]^2>\dfrac{(k+\ell)^2}{2} \Rightarrow (k-\ell)^2>\dfrac{1}{2}](/forum/ext/geomar/texintegr/latexrender/pictures/555d3544514bc8b03cbc5a6a2e499a74.png) , που προφανώς ισχύει.
, που προφανώς ισχύει. ώστε να ισχύει ένα από τα πιο πάτω:
ώστε να ισχύει ένα από τα πιο πάτω: και
και  (θετικός) περιττός.
(θετικός) περιττός. και
και  .
. , ο δεύτερος παίκτης μειώνει το
, ο δεύτερος παίκτης μειώνει το  και διατηρεί
και διατηρεί 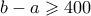 . Το μόνο που μπορεί να κάνει ο πρώτος παίκτης στην επόμενη κίνησή του είναι να μειώσει το
. Το μόνο που μπορεί να κάνει ο πρώτος παίκτης στην επόμενη κίνησή του είναι να μειώσει το  το πολύ κατά
το πολύ κατά  , παρατηρούμε ότι ούτως ή άλλως θα έχει γίνει περιττός αριθμός κινήσεων οπότε το
, παρατηρούμε ότι ούτως ή άλλως θα έχει γίνει περιττός αριθμός κινήσεων οπότε το  θα είναι περιττό. (Αρχικά ισούται με
θα είναι περιττό. (Αρχικά ισούται με  και σε κάθε κίνηση μειώνεται κατά
και σε κάθε κίνηση μειώνεται κατά  ισούται με
ισούται με 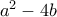 . Στην πρώτη περίπτωση είναι προφανώς αρνητική. Στην δεύτερη έχουμε
. Στην πρώτη περίπτωση είναι προφανώς αρνητική. Στην δεύτερη έχουμε
 .
. και
και  , οπότε
, οπότε 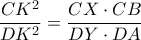 (1).
(1). (2).
(2). .
. , είναι
, είναι  .
. ,
,  , οπότε
, οπότε  συνευθειακά και
συνευθειακά και  συνευθειακά, και επομένως οι
συνευθειακά, και επομένως οι  συντρέχουν στο
συντρέχουν στο  .
. .
. η εξίσωση γράφεται:
η εξίσωση γράφεται:
![\displaystyle{\Delta = (b + c)^2 + 4(b^2 + c^2 + bc) = (b-c)^2 + [2(b+c)]^2} \displaystyle{\Delta = (b + c)^2 + 4(b^2 + c^2 + bc) = (b-c)^2 + [2(b+c)]^2}](/forum/ext/geomar/texintegr/latexrender/pictures/c27d319498eaa3595402776279a9447e.png)
![\displaystyle{(b-c)^2 + [2(b+c)]^2 = z^2 \displaystyle{(b-c)^2 + [2(b+c)]^2 = z^2](/forum/ext/geomar/texintegr/latexrender/pictures/11227e8f971e41c3341f9fe11e9fdcfb.png) για κάποιο θετικό ακέραιο
για κάποιο θετικό ακέραιο  .
. με
με  έχουμε τις πιθανές περιπτώσεις:
έχουμε τις πιθανές περιπτώσεις:![\displaystyle{\begin{Bmatrix} b - c = k(m^2 - n^2)\\ 2(b+c) = k2mn \end{Bmatrix}\Rightarrow \begin{Bmatrix} (b-c)^2 = k^2[(m^2 - n^2)]^2\\ 4(b+c) = k4mn \end{Bmatrix}} \displaystyle{\begin{Bmatrix} b - c = k(m^2 - n^2)\\ 2(b+c) = k2mn \end{Bmatrix}\Rightarrow \begin{Bmatrix} (b-c)^2 = k^2[(m^2 - n^2)]^2\\ 4(b+c) = k4mn \end{Bmatrix}}](/forum/ext/geomar/texintegr/latexrender/pictures/56eec0d7a115befa3da737166e6ec30b.png)
![\displaystyle{k^2[(m^2 - n^2)]^2 > k4mn \Leftrightarrow m^2 - n^2 > 2\sqrt{mn} \Leftrightarrow (m-n)(m + n)> 2\sqrt{mn}} \displaystyle{k^2[(m^2 - n^2)]^2 > k4mn \Leftrightarrow m^2 - n^2 > 2\sqrt{mn} \Leftrightarrow (m-n)(m + n)> 2\sqrt{mn}}](/forum/ext/geomar/texintegr/latexrender/pictures/b74d46d0cfb822de3c662130b10e47d8.png) που ισχύει από
που ισχύει από  και αφού
και αφού  .
.
 που ισχύει προφανώς.
που ισχύει προφανώς. είναι μεσοκάθετος της χορδής
είναι μεσοκάθετος της χορδής  το κέντρο του κύκλου).
το κέντρο του κύκλου). το συμμετρικό του
το συμμετρικό του  και
και  .
. ισοσκελές τραπέζιο και άρα
ισοσκελές τραπέζιο και άρα  .
. προκύπτει το ζητούμενο.
προκύπτει το ζητούμενο. και
και  τα μέσα των
τα μέσα των  αντίστοιχα. Τότε από
αντίστοιχα. Τότε από  παίρνουμε:
παίρνουμε:  Η τελευταία όμως ισχύει,
Η τελευταία όμως ισχύει,  της βάσης
της βάσης  του ισοσκελούς τριγώνου
του ισοσκελούς τριγώνου  έχουμε
έχουμε 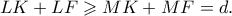
 οριζόντιες και
οριζόντιες και  κάθετες γραμμές. Έστω ότι η κάθετη γραμμή
κάθετες γραμμές. Έστω ότι η κάθετη γραμμή 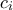 τέμνει
τέμνει  τετράγωνα της διαμέρισης.
τετράγωνα της διαμέρισης.  τετράγωνα τότε πρέπει
τετράγωνα τότε πρέπει  . Πρέπει λοιπόν κάποιο από τα
. Πρέπει λοιπόν κάποιο από τα  να είναι περιττό, έστο το
να είναι περιττό, έστο το  .
. τέμνει
τέμνει  τετράγωνα της διαμέρισης, τότε τέμνει και
τετράγωνα της διαμέρισης, τότε τέμνει και  τετράγωνα της διαμέρισης. Συνολικά τέμνει
τετράγωνα της διαμέρισης. Συνολικά τέμνει  τετράγωνα της διαμέρισης. Δηλαδή περιττό αριθμό τετραγώνων της διαμέρισης όπως θέλαμε να δείξουμε.
τετράγωνα της διαμέρισης. Δηλαδή περιττό αριθμό τετραγώνων της διαμέρισης όπως θέλαμε να δείξουμε. . Η λύση αύριο αν δεν απαντηθεί.
. Η λύση αύριο αν δεν απαντηθεί. , είναι
, είναι  , οπότε έχουμε μία λύση
, οπότε έχουμε μία λύση  .
.  .
. , άρα
, άρα  .
.  ή
ή  , οπότε
, οπότε  ή
ή  .
. .
. .
. , οπότε
, οπότε 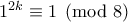 ,
,  ... και
... και  .
. .
. , για κάθε
, για κάθε  , και από την Άπειρη κάθοδο του Fermat πρέπει
, και από την Άπειρη κάθοδο του Fermat πρέπει 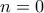 , άτοπο.
, άτοπο. .
. , είναι
, είναι  , άτοπο.
, άτοπο. .
. .
. είναι πρώτος αριθμός, έστω
είναι πρώτος αριθμός, έστω  , έχουμε
, έχουμε  .
. , άτοπο.
, άτοπο. ,
,  και
και  .
. , είναι
, είναι  και όμοια
και όμοια  , και αφού
, και αφού  , που είναι άτοπο, καθώς
, που είναι άτοπο, καθώς  .
.