Θέματα της πρώτης φάσης για την 8η τάξη.
1. Σε ένα βαγόνι καθήμενων βρίσκονται τριθέσια καθίσματα για τους επιβάτες, 20 σειρές των δυο καθισμάτων. Ο Κώστας παρατήρησε, ότι σε κάθε σειρά κάθονται 3 ή 5 άτομα. Ύστερα ο Κώστας υπολόγισε, σε πόσα καθίσματα κάθονται 3 άτομα και σε πόσα ένα άτομο. Να βρείτε το άθροισμα των αριθμών του Κώστα. (Κοχάς)
2. Ποιοι πρώτοι μπορούν να γραφούν στη μορφή

για ακέραια
 ;
;3. Στο διαγαλαξιακό φεστιβάλ «Ουράνιο Τόξο» προσήλθαν 107 πράσινα και μωβ ανθρωπάκια. Τα πράσινα ανθρωπάκια αντιλαμβάνονται σωστά τα χρώματα, δυστυχώς όμως τα μωβ αντιλαμβάνονται το πράσινο ως μωβ και το ανάποδο. Κοιτώντας γύρο, γύρο, κάθε συμμετέχων του φεστιβάλ πλησίασε κάποιον και είπε «Μα τι μωβ που είσαι!» και δώρισε ένα κάκτο. Ποιος είναι ο ελάχιστος αριθμός από ανθρωπάκια που θα μπορούσαν να μην πάρουν ούτε ένα κάκτο; (Τσουχνόβ)
4. Κατά μήκος μαιανδρικού ποταμού βρίσκονται τρεις πόλεις Α, Β και Γ (όχι απαραίτητα με αυτή την σειρά και όχι απαραίτητα στην ίδια ζώνη ώρας). Μεταξύ των πόλεων κινούνται ποταμόπλοια, η ταχύτητα τους είναι 6 φορές μεγαλύτερη της ταχύτητας του ποταμού. Παρακάτω φαίνεται κομμάτι πίνακα δρομολογίων, ή ώρα είναι παντού τοπική, κάθε δρομολόγιο εκτελείται σε μια μέρα.

Η Ναυσικά, βρισκόμενη στην πιο ψηλά εκ των τριών πόλεων (κατά την ροή του ποταμού), πέταξε μια μπάλα. Σε πόση ώρα θα την δουν οι κάτοικοι της πιο χαμηλά βρισκόμενης πόλης, εάν η μπάλα δε βρίσκει εμπόδια κατά το πλου της; (Σόλνιν)
5. Στην πλευρά
 τριγώνου
τριγώνου  δίνεται σημείο
δίνεται σημείο  και στο τμήμα
και στο τμήμα  , σημείο
, σημείο  . Είναι γνωστό ότι
. Είναι γνωστό ότι  . Να αποδείξετε, ότι
. Να αποδείξετε, ότι  . (Σμιρνόβ)
. (Σμιρνόβ)
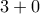 είτε
είτε  είτε
είτε  άτομα. Παρατηρούμε ότι σε κάθε μία από τις σειρές τα καθίσματα στα οποία κάθονται είτε
άτομα. Παρατηρούμε ότι σε κάθε μία από τις σειρές τα καθίσματα στα οποία κάθονται είτε  είτε
είτε  άτομο είναι ακριβώς
άτομο είναι ακριβώς  , όσα και οι σειρές.
, όσα και οι σειρές. .
.  ελέγχουμε με το χέρι. Θα βρούμε τις λύσεις
ελέγχουμε με το χέρι. Θα βρούμε τις λύσεις  και
και  . Για
. Για  η παράσταση ισούται
η παράσταση ισούται  που είνα σύνθετος.
που είνα σύνθετος. γράφουμε
γράφουμε  με
με  . Η παράσταση γίνεται
. Η παράσταση γίνεται  (σύνθετος).
(σύνθετος). , τότε
, τότε  επίσης έχουμε
επίσης έχουμε  Συνεπώς η πλευρά
Συνεπώς η πλευρά 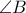 είναι μεγαλύτερη των
είναι μεγαλύτερη των 
 είναι
είναι  . Έχουμε δεδομένο ότι
. Έχουμε δεδομένο ότι  οπότε
οπότε 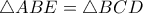 .
. άρα
άρα  , με συνέπεια
, με συνέπεια  , άρα
, άρα  .
.
 την ταχύτητα του ποταμού και
την ταχύτητα του ποταμού και  το μήκος της διαδρομής (μέσω του ποταμού) από την πόλη που βρίσκεται ψηλότερα έως την πόλη που βρίσκεται χαμηλότερα (μεταξύ των πόλεων Α,Β,Γ).
το μήκος της διαδρομής (μέσω του ποταμού) από την πόλη που βρίσκεται ψηλότερα έως την πόλη που βρίσκεται χαμηλότερα (μεταξύ των πόλεων Α,Β,Γ). και ο χρόνος που ανεβαίνει είναι
και ο χρόνος που ανεβαίνει είναι  . (η σχετική ταχύτητα του ποταμόπλοιου είναι εξαπλάσια από την ταχύτητα του ποταμού ).
. (η σχετική ταχύτητα του ποταμόπλοιου είναι εξαπλάσια από την ταχύτητα του ποταμού ). , ο χρόνος που χρειάζεται η μπάλα για να πάει από την πόλη που είναι ψηλότερα στην πόλη που είναι χαμηλότερα είναι
, ο χρόνος που χρειάζεται η μπάλα για να πάει από την πόλη που είναι ψηλότερα στην πόλη που είναι χαμηλότερα είναι  ώρες.
ώρες. πράσινα ανθρωπάκια και
πράσινα ανθρωπάκια και  μωβ τα οποία συμβολίζουμε με
μωβ τα οποία συμβολίζουμε με  και
και  αντίστοιχα. Για
αντίστοιχα. Για  τα
τα  και
και  ανταλλάζουν κάκτους. Επίσης το
ανταλλάζουν κάκτους. Επίσης το  δίνει κάκτο στο
δίνει κάκτο στο 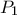 . Άρα όλα τσα ανθρωπάκια πήραν κάκτο εκτός από το
. Άρα όλα τσα ανθρωπάκια πήραν κάκτο εκτός από το