Να βρείτε όλες τις θετικοί ακέραιες λύσεις
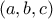 της εξίσωσης
της εξίσωσης
Προβλήμα 2
Αν
 είναι θετικοί πραγματικοί αριθμοί , να δείξετε ότι
είναι θετικοί πραγματικοί αριθμοί , να δείξετε ότι
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
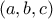 της εξίσωσης
της εξίσωσης
 είναι θετικοί πραγματικοί αριθμοί , να δείξετε ότι
είναι θετικοί πραγματικοί αριθμοί , να δείξετε ότι
Μου φάνηκε λίγο πιο βατή από την άλλη, η οποία, δεν ξέρω, λύνεται με κάποιο θεώρημα; Τα προσπάθησα όλα, αλλά δεν το κατάφερα...JimNt. έγραψε:Tην δεύτερη την έχω ξανασυναντήσει. Έπειτα από την εκτέλεση των πράξεων προκύπτει κάτι αληθές.
Κατά λάθος το έγραψα. Έχει διορθωθεί!JimNt. έγραψε:Φιλικά... Καμία άσηση Θ.Αριθμών δεν λύνεται με πράξεις...
Θεωρήματα... Δεν βρήκα κάποιο που να βοηθάει!JimNt. έγραψε:Τι ακριβώς προσπάθησες;
 , άλλα το μόνο που κατάφερα με την πρώτη άσκηση ήταν να αποδείξω ότι
, άλλα το μόνο που κατάφερα με την πρώτη άσκηση ήταν να αποδείξω ότι  είναι περιττοί και μάλιστα ότι
είναι περιττοί και μάλιστα ότι  . Τίποτα άλλο σημαντικό.
. Τίποτα άλλο σημαντικό. , άρα δεν μπορούμε να χρησιμοποιήσουμε κάποια κλασική μέθοδο που να αποδεικνύει ότι η εξίσωση είναι άλυτη. Πρέπει να εκμεταλλευτούμε το γεγονός του ότι a, b, c<2 (εκτός αν υπάρχει και άλλη λύση).
, άρα δεν μπορούμε να χρησιμοποιήσουμε κάποια κλασική μέθοδο που να αποδεικνύει ότι η εξίσωση είναι άλυτη. Πρέπει να εκμεταλλευτούμε το γεγονός του ότι a, b, c<2 (εκτός αν υπάρχει και άλλη λύση).Έφτασα κι εγώ εκεί. Τι βγάζει;Διονύσιος Αδαμόπουλος έγραψε:Πάλεψα με πολλά, άλλα το μόνο που κατάφερα με την πρώτη άσκηση ήταν να αποδείξω ότι
είναι περιττοί και μάλιστα ότι
. Τίποτα άλλο σημαντικό.
Θα δείξουμε ότι η μόνη λύση είναι ηDatis-Kalali έγραψε:Προβλήμα 1
Να βρείτε όλες τις θετικοί ακέραιες λύσειςτης εξίσωσης

 . Κάπως επιγραμματικά διότι η λύση είναι αρκετά μεγάλη:
. Κάπως επιγραμματικά διότι η λύση είναι αρκετά μεγάλη: βγαίνει
βγαίνει  .
. βγαίνει
βγαίνει  .
. βγαίνει
βγαίνει  .
. και τα πιο πάνω έχουμε
και τα πιο πάνω έχουμε  , και
, και  . Πρέπει
. Πρέπει  και
και  . Καταλήγουμε στο
. Καταλήγουμε στο 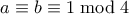 .
. και χρησιμοποιώντας τα προηγούμενα παίρνουμε
και χρησιμοποιώντας τα προηγούμενα παίρνουμε  .
. είναι περιοδικά
είναι περιοδικά  .
.  είναι περιοδικά
είναι περιοδικά  .
. και
και  παίρνουμε
παίρνουμε  η
η 
 : Τότε
: Τότε  . Αν
. Αν 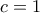 , τότε
, τότε  . Αν
. Αν  τότε έχουμε άτοπο
τότε έχουμε άτοπο  αφού
αφού  η ακολουθία
η ακολουθία  είναι περιοδικά
είναι περιοδικά 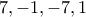 .
.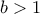 τότε
τότε  .
. είναι περιοδικά
είναι περιοδικά  .
. τότε
τότε  και άρα
και άρα  . Επειδή επιπλέον
. Επειδή επιπλέον  και η ακολουθία
και η ακολουθία  είναι περιοδικά
είναι περιοδικά  τότε καταλήγουμε στο
τότε καταλήγουμε στο  ή
ή 
 . Πρέπει
. Πρέπει 
 είναι περιοδικά
είναι περιοδικά  .
.  είναι περιοδικά
είναι περιοδικά  .
. είναι περιοδικά
είναι περιοδικά  .
. όσο και η
όσο και η  καταλήγουν σε άτοπο.
καταλήγουν σε άτοπο.Demetres έγραψε:Θα δείξουμε ότι η μόνη λύση είναι ηDatis-Kalali έγραψε:Προβλήμα 1
Να βρείτε όλες τις θετικοί ακέραιες λύσειςτης εξίσωσης

. Κάπως επιγραμματικά διότι η λύση είναι αρκετά μεγάλη:
Μεβγαίνει
.
Μεβγαίνει
.
Μεβγαίνει
.
Μεκαι τα πιο πάνω έχουμε
, και
. Πρέπει
και
. Καταλήγουμε στο
.
Μεκαι χρησιμοποιώντας τα προηγούμενα παίρνουμε
.
Η ακολουθίαείναι περιοδικά
.
Η ακολουθίαείναι περιοδικά
.
Χρησιμοποιώντας ότικαι
παίρνουμε
η
Περίπτωση 1: Αν: Τότε
. Αν
, τότε
. Αν
τότε έχουμε άτοπο
αφού
η ακολουθία
είναι περιοδικά
.
Περίπτωση 2: Αντότε
.
Η ακολουθίαείναι περιοδικά
.
Αφούτότε
και άρα
. Επειδή επιπλέον
και η ακολουθία
είναι περιοδικά
τότε καταλήγουμε στο
ή
Τώρα δουλεύουμε. Πρέπει
Η ακολουθίαείναι περιοδικά
.
Η ακολουθίαείναι περιοδικά
.
Η ακολουθίαείναι περιοδικά
.
Όμως τόσο η περίπτωσηόσο και η
καταλήγουν σε άτοπο.
Από τις παραπάνω λύσεις, φαίνεται ότι η άσκηση αυτή, μόνο για Junior δεν είναι!silouan έγραψε:Μια διαφορετική λύση εδώ:
https://artofproblemsolving.com/community/c6h353444
Η προς απόδειξη γράφεταιDatis-Kalali έγραψε:Προβλήμα 2
Ανείναι θετικοί πραγματικοί αριθμοί , να δείξετε ότι
 .
. για οποιαδήποτε
για οποιαδήποτε  .
. .
. η ισοδύναμα,
η ισοδύναμα, , που μετά τις πράξεις (!) δίνει
, που μετά τις πράξεις (!) δίνει  , που ισχύει.
, που ισχύει. .
.Το 2 ήταν και εδώDatis-Kalali έγραψε:
Προβλήμα 2
Ανείναι θετικοί πραγματικοί αριθμοί , να δείξετε ότι
Μέλη σε αυτήν τη Δ. Συζήτηση: Google [Bot], MSN [Bot] και 14 επισκέπτες