Δίνεται η εξίσωση:

Αν ο αριθμός
 είναι λύση της εξίσωσης
είναι λύση της εξίσωσης  , να αποδείξετε ότι ο αριθμός
, να αποδείξετε ότι ο αριθμός  είναι επίσης ρίζα της εξίσωσης
είναι επίσης ρίζα της εξίσωσης  .
.Πρόβλημα 2
Δίνεται τρίγωνο
 . Πάνω στις πλευρές του
. Πάνω στις πλευρές του  και
και  παίρνουμε σημεία
παίρνουμε σημεία  και
και 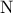 , αντίστοιχα, τέτοια ώστε
, αντίστοιχα, τέτοια ώστε 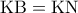 . Η εσωτερική διχοτόμος της γωνίας
. Η εσωτερική διχοτόμος της γωνίας 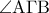 τέμνει τον περιγεγραμμένο κύκλο του τριγώνου
τέμνει τον περιγεγραμμένο κύκλο του τριγώνου  στα σημεία
στα σημεία  και
και 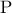 . Αν η κάθετη από το
. Αν η κάθετη από το 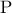 πάνω στην
πάνω στην  τέμνει το ευθύγραμμο τμήμα
τέμνει το ευθύγραμμο τμήμα 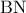 στο
στο 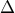 , να αποδείξετε ότι
, να αποδείξετε ότι  .
.Πρόβλημα 3
Στον πίνακα είναι γραμμένοι οι αριθμοί
 και
και  . Κάποιος παίζει το εξής παιχνίδι, ακολουθώντας τα πιο κάτω βήματα:
. Κάποιος παίζει το εξής παιχνίδι, ακολουθώντας τα πιο κάτω βήματα:Βήμα 1: Διαγράφει από τον πίνακα δύο από τους αριθμούς
 (έστω ότι διαγράφει τους αριθμούς
(έστω ότι διαγράφει τους αριθμούς  ) και στη θέση τους γράφει τους αριθμούς
) και στη θέση τους γράφει τους αριθμούς 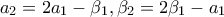 .
.Βήμα 2: Διαγράφει από τον πίνακα δύο από τους αριθμούς
 (έστω ότι διαγράφει τους αριθμούς
(έστω ότι διαγράφει τους αριθμούς 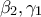 ) και στη θέση τους γράφει τους αριθμούς
) και στη θέση τους γράφει τους αριθμούς  .
.Τότε, στον πίνακα είναι γραμμένοι οι αριθμοί
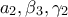 . Η ίδια διαδικασία επαναλαμβάνεται και στα επόμενα βήματα.
. Η ίδια διαδικασία επαναλαμβάνεται και στα επόμενα βήματα.Να εξετάσετε αν μετά από κάποιο πλήθος βημάτων είναι δυνατόν οι δύο από τους τρεις αριθμούς που είναι γραμμένοι στον πίνακα να είναι ταυτόχρονα ίσοι με το μηδέν.
Πρόβλημα 4
Να βρείτε όλους τους τετραψήφιους φυσικούς αριθμούς
 , έτσι ώστε οι αριθμοί
, έτσι ώστε οι αριθμοί  και
και 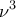 (γραμμένοι στο δεκαδικό σύστημα αρίθμησης) να έχουν ίδιο το τελευταίο τετραψήφιο τμήμα τους, το οποίο να είναι διαφορετικό του
(γραμμένοι στο δεκαδικό σύστημα αρίθμησης) να έχουν ίδιο το τελευταίο τετραψήφιο τμήμα τους, το οποίο να είναι διαφορετικό του  .
.(Δηλαδή, αν το τελευταίο τετραψήφιο τμήμα των
 και
και 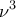 είναι
είναι  , τότε
, τότε  .)
.)Επεξεργασία: Έγινε διόρθωση της εκφώνησης του προβλήματος 1.

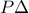 είναι μεσοκάθετος του
είναι μεσοκάθετος του  και άρα
και άρα  δηλ. το
δηλ. το  είναι εγγράψιμο και το ζητούμενο έπεται.
είναι εγγράψιμο και το ζητούμενο έπεται. , γράφουμε στον πίνακα τους
, γράφουμε στον πίνακα τους 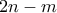 ,
, 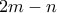 ; Σε περίπτωση που αυτό όντως ισχύει δεν θα είναι σχετικά απλό για τον λύτη να παρατηρήσει ότι αν ότι οι αριθμοί που προκύπτουν έπειτα από κάθε περίπτωση είναι ένας προς ένας ισοϋπόλοιποι
; Σε περίπτωση που αυτό όντως ισχύει δεν θα είναι σχετικά απλό για τον λύτη να παρατηρήσει ότι αν ότι οι αριθμοί που προκύπτουν έπειτα από κάθε περίπτωση είναι ένας προς ένας ισοϋπόλοιποι  με τους
με τους  προηγούμενους (δηλαδή αν δοθούν
προηγούμενους (δηλαδή αν δοθούν 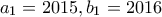 και
και  . Κάποιος παίζει το εξής παιχνίδι, ακολουθώντας τα πιο κάτω βήματα:
. Κάποιος παίζει το εξής παιχνίδι, ακολουθώντας τα πιο κάτω βήματα: (έστω ότι διαγράφει τους αριθμούς
(έστω ότι διαγράφει τους αριθμούς  ) και στη θέση τους γράφει τους αριθμούς
) και στη θέση τους γράφει τους αριθμούς 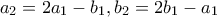 .
. (έστω ότι διαγράφει τους αριθμούς
(έστω ότι διαγράφει τους αριθμούς 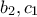 ) και στη θέση τους γράφει τους αριθμούς
) και στη θέση τους γράφει τους αριθμούς  .
. . Η ίδια διαδικασία επαναλαμβάνεται και στα επόμενα βήματα.
. Η ίδια διαδικασία επαναλαμβάνεται και στα επόμενα βήματα.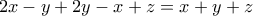
 πάνω στον πίνακα.
πάνω στον πίνακα. πάνω στον πίνακα.
πάνω στον πίνακα. , έτσι ώστε οι αριθμοί
, έτσι ώστε οι αριθμοί 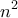 και
και  (γραμμένοι στο δεκαδικό σύστημα αρίθμησης) να έχουν ίδιο το τελευταίο τετραψήφιο τμήμα τους, το οποίο να είναι διαφορετικό του
(γραμμένοι στο δεκαδικό σύστημα αρίθμησης) να έχουν ίδιο το τελευταίο τετραψήφιο τμήμα τους, το οποίο να είναι διαφορετικό του 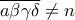 .)
.)


 αφού
αφού 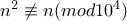

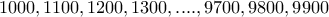
 . Θα αφήσω όμως λίγο χρόνο πριν βάλω πλήρη λύση για να βρεις που έγινε το λάθος.
. Θα αφήσω όμως λίγο χρόνο πριν βάλω πλήρη λύση για να βρεις που έγινε το λάθος.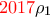 είναι λύση της εξίσωσης
είναι λύση της εξίσωσης 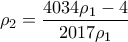 είναι επίσης ρίζα της εξίσωσης
είναι επίσης ρίζα της εξίσωσης  , με
, με  (1)
(1) .
.
 (2).
(2).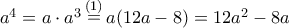 , και αντικαθιστώντας,
, και αντικαθιστώντας, 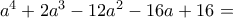
 .
.
 , που δίνει το ζητούμενο.
, που δίνει το ζητούμενο.