ΕΥΚΛΕΙΔΗΣ 2016
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5561
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
ΕΥΚΛΕΙΔΗΣ 2016
Εδώ τα θέματα του ΕΥΚΛΕΙΔΗ 2016 και η επεξεργασία τους !
Καλά αποτελέσματα !
Καλά αποτελέσματα !
- Συνημμένα
-
- 2016 THEMATA_EYKLEIDH_16_01_2016 (1).pdf
- (316.67 KiB) Μεταφορτώθηκε 2880 φορές
Re: ΕΥΚΛΕΙΔΗΣ 2016
ΘΕΜΑ 1/Β ΛΥΚΕΙΟΥ
Η κοινή διαφορά της αριθμητικής προόδου είναι
(α) Συνεπώς, το άθροισμα των πρώτων όρων της είναι
πρώτων όρων της είναι

(β) Ο μέσος όρος των πρώτων όρων της πρόδου είναι
πρώτων όρων της πρόδου είναι  , που ισούται με
, που ισούται με  αν και μόνο αν
αν και μόνο αν 
Edit: Στην παραπάνω λύση κάναμε την υπόθεση ότι η παράσταση είναι ακέραια. Αλλιώς,θα πρέπει να είναι , (όχι απλώς
, (όχι απλώς  ) και άρα
) και άρα  .
.
Φιλικά,
Αχιλλέας
Η κοινή διαφορά της αριθμητικής προόδου είναι

(α) Συνεπώς, το άθροισμα των
 πρώτων όρων της είναι
πρώτων όρων της είναι
(β) Ο μέσος όρος των
 πρώτων όρων της πρόδου είναι
πρώτων όρων της πρόδου είναι  , που ισούται με
, που ισούται με  αν και μόνο αν
αν και μόνο αν 
Edit: Στην παραπάνω λύση κάναμε την υπόθεση ότι η παράσταση είναι ακέραια. Αλλιώς,θα πρέπει να είναι
 , (όχι απλώς
, (όχι απλώς  ) και άρα
) και άρα  .
.Φιλικά,
Αχιλλέας
τελευταία επεξεργασία από achilleas σε Σάβ Ιαν 16, 2016 12:56 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Re: ΕΥΚΛΕΙΔΗΣ 2016
ΘΕΜΑ 2/Β ΛΥΚΕΙΟΥ
Προφανώς .
.
Η δοθείσα εξίσωση γράφεται

Διαιρώντας την τελευταία εξίσωση με παίρνουμε
παίρνουμε
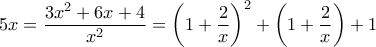 . (*)
. (*)
Θέτοντας , δηλ.
, δηλ.  , από την (*) παίρνουμε
, από την (*) παίρνουμε
 ,
,
Δηλ. , ή
, ή ![r=\sqrt[3]{11} r=\sqrt[3]{11}](/forum/ext/geomar/texintegr/latexrender/pictures/307051808e7a7c5cf1b9ce2987d9d2d7.png) .
.
Συνεπώς,![x=\dfrac{2}{\sqrt[3]{11}-1} x=\dfrac{2}{\sqrt[3]{11}-1}](/forum/ext/geomar/texintegr/latexrender/pictures/67ba031c2b12ec1cb7e4edf5a4a7cde3.png) .
.
Φιλικά,
Αχιλλέας
Προφανώς
 .
. Η δοθείσα εξίσωση γράφεται

Διαιρώντας την τελευταία εξίσωση με
 παίρνουμε
παίρνουμε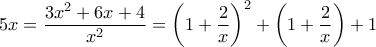 . (*)
. (*)Θέτοντας
 , δηλ.
, δηλ.  , από την (*) παίρνουμε
, από την (*) παίρνουμε  ,
, Δηλ.
 , ή
, ή ![r=\sqrt[3]{11} r=\sqrt[3]{11}](/forum/ext/geomar/texintegr/latexrender/pictures/307051808e7a7c5cf1b9ce2987d9d2d7.png) .
.Συνεπώς,
![x=\dfrac{2}{\sqrt[3]{11}-1} x=\dfrac{2}{\sqrt[3]{11}-1}](/forum/ext/geomar/texintegr/latexrender/pictures/67ba031c2b12ec1cb7e4edf5a4a7cde3.png) .
.Φιλικά,
Αχιλλέας
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13278
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: ΕΥΚΛΕΙΔΗΣ 2016
Α' Λυκείου Πρόβλημα 3
Η διάμεσος του τριγώνου
του τριγώνου  τέμνει την
τέμνει την  στο
στο  . Προφανώς είναι
. Προφανώς είναι  και επειδή
και επειδή  , θα είναι και
, θα είναι και  . Άρα και το
. Άρα και το  είναι ισόπλευρο.
είναι ισόπλευρο.
Εύκολα τώρα διαπιστώνουμε ότι τα τρίγωνα είναι ίσα, οπότε το τετράπλευρο
είναι ίσα, οπότε το τετράπλευρο  είναι ρόμβος και
είναι ρόμβος και  , δηλαδή
, δηλαδή  .
.
Η διάμεσος
 του τριγώνου
του τριγώνου  τέμνει την
τέμνει την  στο
στο  . Προφανώς είναι
. Προφανώς είναι  και επειδή
και επειδή  , θα είναι και
, θα είναι και  . Άρα και το
. Άρα και το  είναι ισόπλευρο.
είναι ισόπλευρο.Εύκολα τώρα διαπιστώνουμε ότι τα τρίγωνα
 είναι ίσα, οπότε το τετράπλευρο
είναι ίσα, οπότε το τετράπλευρο  είναι ρόμβος και
είναι ρόμβος και  , δηλαδή
, δηλαδή  .
.Re: ΕΥΚΛΕΙΔΗΣ 2016
Γεωμετρία Α λυκείου 3 άσκηση .
Καλημέρα από το σχολείο μου που είναι και εξεταστικό κέντρο.
Τα τρίγωνα έχουν
έχουν  .
.
Κατά συνέπεια τα πιο πάνω τρίγωνα είναι ίσα , οπότε .
.
Όμως (εξωτερική στο τρίγωνο
(εξωτερική στο τρίγωνο  ) . Άρα
) . Άρα  .
.
Αφού όμως το τρίγωνο είναι ισοσκελές θα έχει τις γωνίες της βάσης του
είναι ισοσκελές θα έχει τις γωνίες της βάσης του  από
από  και έτσι
και έτσι  .
.
Νίκος
Καλημέρα από το σχολείο μου που είναι και εξεταστικό κέντρο.
Τα τρίγωνα
 έχουν
έχουν  .
.Κατά συνέπεια τα πιο πάνω τρίγωνα είναι ίσα , οπότε
 .
.Όμως
 (εξωτερική στο τρίγωνο
(εξωτερική στο τρίγωνο  ) . Άρα
) . Άρα  .
. Αφού όμως το τρίγωνο
 είναι ισοσκελές θα έχει τις γωνίες της βάσης του
είναι ισοσκελές θα έχει τις γωνίες της βάσης του  από
από  και έτσι
και έτσι  .
.Νίκος
τελευταία επεξεργασία από Doloros σε Σάβ Ιαν 16, 2016 10:34 am, έχει επεξεργασθεί 1 φορά συνολικά.
- nkatsipis
- Επιμελητής
- Δημοσιεύσεις: 778
- Εγγραφή: Κυρ Δεκ 21, 2008 10:26 am
- Τοποθεσία: Σαντορίνη
- Επικοινωνία:
Re: ΕΥΚΛΕΙΔΗΣ 2016
 Πρόβλημα 2/ Β Γυμνασίου
Πρόβλημα 2/ Β Γυμνασίου Έχουμε οτι:

Η απάντηση ειναι ο αριθμός
 , διότι αφού
, διότι αφού  , τότε:
, τότε: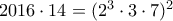 και
και  .
.Νίκος Κατσίπης
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: ΕΥΚΛΕΙΔΗΣ 2016
Θέμα 4/Β Λυκείου
Καταρχήν παρατηρούμε ότι εάν ένα ζεύγος είναι λύση, τότε και τα άπειρα ζεύγη
είναι λύση, τότε και τα άπειρα ζεύγη  με
με  θετικό ακέραιο, είναι επίσης λύσεις. Άρα μπορούμε να βρούμε τα ζεύγη
θετικό ακέραιο, είναι επίσης λύσεις. Άρα μπορούμε να βρούμε τα ζεύγη  με τα
με τα  να είναι πρώτοι μεταξύ τους.
να είναι πρώτοι μεταξύ τους.
Θέλουμε λοιπόν

άρα κι επειδή
κι επειδή  άρα
άρα  απ' όπου
απ' όπου  ή
ή  .
.
Επίσης
 απ' όπου
απ' όπου 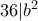
άρα οπότε
οπότε  . Αντικαθιστώντας έχουμε
. Αντικαθιστώντας έχουμε  για κάποιο θετικό ακέραιο
για κάποιο θετικό ακέραιο  απ' όπου
απ' όπου  κι επειδή
κι επειδή  άρα
άρα  απ' όπου
απ' όπου  .
.
Άρα οι λύσεις με είναι οι
είναι οι  που είναι δεκτές κι έτσι οι λύσεις της αρχικής είναι οι
που είναι δεκτές κι έτσι οι λύσεις της αρχικής είναι οι  για
για  θετικό ακέραιο.
θετικό ακέραιο.
Αλέξανδρος
Καταρχήν παρατηρούμε ότι εάν ένα ζεύγος
 είναι λύση, τότε και τα άπειρα ζεύγη
είναι λύση, τότε και τα άπειρα ζεύγη  με
με  θετικό ακέραιο, είναι επίσης λύσεις. Άρα μπορούμε να βρούμε τα ζεύγη
θετικό ακέραιο, είναι επίσης λύσεις. Άρα μπορούμε να βρούμε τα ζεύγη  με τα
με τα  να είναι πρώτοι μεταξύ τους.
να είναι πρώτοι μεταξύ τους.Θέλουμε λοιπόν

άρα
 κι επειδή
κι επειδή  άρα
άρα  απ' όπου
απ' όπου  ή
ή  .
.Επίσης
 απ' όπου
απ' όπου 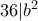
άρα
 οπότε
οπότε  . Αντικαθιστώντας έχουμε
. Αντικαθιστώντας έχουμε  για κάποιο θετικό ακέραιο
για κάποιο θετικό ακέραιο  απ' όπου
απ' όπου  κι επειδή
κι επειδή  άρα
άρα  απ' όπου
απ' όπου  .
.Άρα οι λύσεις με
 είναι οι
είναι οι  που είναι δεκτές κι έτσι οι λύσεις της αρχικής είναι οι
που είναι δεκτές κι έτσι οι λύσεις της αρχικής είναι οι  για
για  θετικό ακέραιο.
θετικό ακέραιο.Αλέξανδρος
Αλέξανδρος Συγκελάκης
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13278
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: ΕΥΚΛΕΙΔΗΣ 2016
Α ΛΥΚΕΙΟΥ ΘΕΜΑ 3ο
Για πλουραλισμό λύσεων, βάζω μόνο το σχήμα.
Η γωνία ΒΚΖ είναι
Για πλουραλισμό λύσεων, βάζω μόνο το σχήμα.
Η γωνία ΒΚΖ είναι

Γιατί πάντα αριθμόν έχοντι. Άνευ τούτου ουδέν νοητόν και γνωστόν.
Re: ΕΥΚΛΕΙΔΗΣ 2016
ΘΕΜΑ 4/Γ ΓΥΜΝΑΣΙΟΥ
Έστω ότι το Γιάννης παίρνει καραμέλες από τις οποίες κρατάει τις
καραμέλες από τις οποίες κρατάει τις  και δίνει στο Βαγγέλη τα
και δίνει στο Βαγγέλη τα 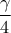 .
.
Επειδή ο καθένας έχει ακέραιο αριθμό καραμελών σε αυτή τη μοιρασιά, πρέπει το να είναι πολ/σιο του 4.
να είναι πολ/σιο του 4.
Έστω ότι ο Βαγγέλης παίρνει καραμέλες, κρατάει τις
καραμέλες, κρατάει τις  και δίνει
και δίνει  στο Γιάννη.
στο Γιάννη.
Επειδή ο καθένας έχει ακέραιο αριθμό καραμελών σε αυτή τη μοιρασιά, πρέπει το να είναι πολ/σιο του 12.
να είναι πολ/σιο του 12.
Ο Γιάννης, λοιπόν, θα έχει καραμέλες,
καραμέλες,
και ο Βαγγέλης, θα έχει καραμέλες.
καραμέλες.
Αφού ο Γιάννης θα έχει τελικά εξαπλάσιες καραμέλες από το Βαγγέλη, είναι ,
,
δηλ. .
.
Οι ελάχιστοι θετικοί ακέραιοι που ικανοποιούν τις παραπάνω συνθήκες είναι και
και  , οπότε η σακούλα περιέχει τουλάχιστον
, οπότε η σακούλα περιέχει τουλάχιστον  καραμέλες.
καραμέλες.
Φιλικά,
Αχιλλέας
Έστω ότι το Γιάννης παίρνει
 καραμέλες από τις οποίες κρατάει τις
καραμέλες από τις οποίες κρατάει τις  και δίνει στο Βαγγέλη τα
και δίνει στο Βαγγέλη τα 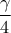 .
.Επειδή ο καθένας έχει ακέραιο αριθμό καραμελών σε αυτή τη μοιρασιά, πρέπει το
 να είναι πολ/σιο του 4.
να είναι πολ/σιο του 4.Έστω ότι ο Βαγγέλης παίρνει
 καραμέλες, κρατάει τις
καραμέλες, κρατάει τις  και δίνει
και δίνει  στο Γιάννη.
στο Γιάννη.Επειδή ο καθένας έχει ακέραιο αριθμό καραμελών σε αυτή τη μοιρασιά, πρέπει το
 να είναι πολ/σιο του 12.
να είναι πολ/σιο του 12.Ο Γιάννης, λοιπόν, θα έχει
 καραμέλες,
καραμέλες, και ο Βαγγέλης, θα έχει
 καραμέλες.
καραμέλες.Αφού ο Γιάννης θα έχει τελικά εξαπλάσιες καραμέλες από το Βαγγέλη, είναι
 ,
,δηλ.
 .
.Οι ελάχιστοι θετικοί ακέραιοι που ικανοποιούν τις παραπάνω συνθήκες είναι
 και
και  , οπότε η σακούλα περιέχει τουλάχιστον
, οπότε η σακούλα περιέχει τουλάχιστον  καραμέλες.
καραμέλες.Φιλικά,
Αχιλλέας
Re: ΕΥΚΛΕΙΔΗΣ 2016
ΘΕΜΑ 2/Γ ΓΥΜΝΑΣΙΟΥ
(α) Είναι .
.
(β) Είναι αν και μόνο αν
αν και μόνο αν  .
.
Με , είναι από το (α) παίρνουμε
, είναι από το (α) παίρνουμε

Πολ/ντας την παραπάνω με παίρνουμε
παίρνουμε

Φιλικά,
Αχιλλέας
(α) Είναι
 .
.(β) Είναι
 αν και μόνο αν
αν και μόνο αν  .
.Με
 , είναι από το (α) παίρνουμε
, είναι από το (α) παίρνουμε 
Πολ/ντας την παραπάνω με
 παίρνουμε
παίρνουμε
Φιλικά,
Αχιλλέας
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13278
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: ΕΥΚΛΕΙΔΗΣ 2016
Β' Λυκείου Πρόβλημα 3
Η τέμνει τη
τέμνει τη  στο
στο  . Είναι
. Είναι  , και επειδή το
, και επειδή το  είναι μέσο του
είναι μέσο του  , θα είναι
, θα είναι  . Άρα το
. Άρα το  είναι παραλληλόγραμμο. Αλλά το
είναι παραλληλόγραμμο. Αλλά το  είναι ισοσκελές τραπέζιο(τραπέζιο εγγεγραμμένο σε κύκλο), οπότε
είναι ισοσκελές τραπέζιο(τραπέζιο εγγεγραμμένο σε κύκλο), οπότε  και επειδή δεν είναι παράλληλες, το
και επειδή δεν είναι παράλληλες, το  είναι ισοσκελές τραπέζιο.
είναι ισοσκελές τραπέζιο.
Η
 τέμνει τη
τέμνει τη  στο
στο  . Είναι
. Είναι  , και επειδή το
, και επειδή το  είναι μέσο του
είναι μέσο του  , θα είναι
, θα είναι  . Άρα το
. Άρα το  είναι παραλληλόγραμμο. Αλλά το
είναι παραλληλόγραμμο. Αλλά το  είναι ισοσκελές τραπέζιο(τραπέζιο εγγεγραμμένο σε κύκλο), οπότε
είναι ισοσκελές τραπέζιο(τραπέζιο εγγεγραμμένο σε κύκλο), οπότε  και επειδή δεν είναι παράλληλες, το
και επειδή δεν είναι παράλληλες, το  είναι ισοσκελές τραπέζιο.
είναι ισοσκελές τραπέζιο.Re: ΕΥΚΛΕΙΔΗΣ 2016
ΘΕΜΑ 2/Α ΛΥΚΕΙΟΥ
Η διακρίνουσα του τριωνύμου είναι
Παρατηρούμε ότι ο αριθμός λήγει σε 6, όπως και ο αριθμός
λήγει σε 6, όπως και ο αριθμός  .
.
Συνεπώς, η λήγει σε 2. Αλλά δεν υπάρχει τέλειο τετράγωνο ακεραίου που να λήγει σε 2, οπότε η διακρίνουσα δεν είναι τέλειο τετράγωνο ακεραίου.
λήγει σε 2. Αλλά δεν υπάρχει τέλειο τετράγωνο ακεραίου που να λήγει σε 2, οπότε η διακρίνουσα δεν είναι τέλειο τετράγωνο ακεραίου.
Συνεπώς, η εξίσωση δεν έχει ρητή ρίζα.
Φιλικά,
Αχιλλέας
Η διακρίνουσα του τριωνύμου είναι

Παρατηρούμε ότι ο αριθμός
 λήγει σε 6, όπως και ο αριθμός
λήγει σε 6, όπως και ο αριθμός  .
.Συνεπώς, η
 λήγει σε 2. Αλλά δεν υπάρχει τέλειο τετράγωνο ακεραίου που να λήγει σε 2, οπότε η διακρίνουσα δεν είναι τέλειο τετράγωνο ακεραίου.
λήγει σε 2. Αλλά δεν υπάρχει τέλειο τετράγωνο ακεραίου που να λήγει σε 2, οπότε η διακρίνουσα δεν είναι τέλειο τετράγωνο ακεραίου.Συνεπώς, η εξίσωση δεν έχει ρητή ρίζα.
Φιλικά,
Αχιλλέας
Re: ΕΥΚΛΕΙΔΗΣ 2016
Β Λυκείου 3 άσκηση
Λίγο συνοπτικά.
Ας είναι το, άλλο , σημείο τομής της
το, άλλο , σημείο τομής της  με τον
με τον  . το τετράπλευρο
. το τετράπλευρο  είναι ορθογώνιο.
είναι ορθογώνιο.
Από την ισότητα των ορθογωνίων τριγώνων έχουμε
έχουμε  και έτσι τα τετράπλευρα
και έτσι τα τετράπλευρα  είναι παραλληλόγραμμα.
είναι παραλληλόγραμμα.
Αφού όμως το εγγεγραμμένο στο κύκλο τραπέζιο είναι ισοσκελές θα είναι
είναι ισοσκελές θα είναι
 και έτσι το και το τετράπλευρο
και έτσι το και το τετράπλευρο  είναι ισοσκελές τραπέζιο .
είναι ισοσκελές τραπέζιο .
Νίκος
Λίγο συνοπτικά.
Ας είναι
 το, άλλο , σημείο τομής της
το, άλλο , σημείο τομής της  με τον
με τον  . το τετράπλευρο
. το τετράπλευρο  είναι ορθογώνιο.
είναι ορθογώνιο.Από την ισότητα των ορθογωνίων τριγώνων
 έχουμε
έχουμε  και έτσι τα τετράπλευρα
και έτσι τα τετράπλευρα  είναι παραλληλόγραμμα.
είναι παραλληλόγραμμα.Αφού όμως το εγγεγραμμένο στο κύκλο τραπέζιο
 είναι ισοσκελές θα είναι
είναι ισοσκελές θα είναι  και έτσι το και το τετράπλευρο
και έτσι το και το τετράπλευρο  είναι ισοσκελές τραπέζιο .
είναι ισοσκελές τραπέζιο .Νίκος
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: ΕΥΚΛΕΙΔΗΣ 2016
1ο της Γ Λυκείου:
Η διαφορά της προόδου είναι
Άρα ο μέσος όρος του αθροίσματος των
των  πρώτων όρων της προόδου είναι ίσο με
πρώτων όρων της προόδου είναι ίσο με 
Αφού η παραπάνω παράσταση είναι για κάθε τετράγωνο παράστασης του
τετράγωνο παράστασης του  , άρα πρέπει η διακρίνουσα
, άρα πρέπει η διακρίνουσα  να είναι μη θετική, απ΄ όπου
να είναι μη θετική, απ΄ όπου  δηλαδή
δηλαδή  .
.
και τότε επιλέγουμε για τις συγκεκριμένες τιμές του
 ως παράσταση του
ως παράσταση του  την
την  .
.
Αλέξανδρος
Η διαφορά της προόδου είναι

Άρα ο μέσος όρος του αθροίσματος
 των
των  πρώτων όρων της προόδου είναι ίσο με
πρώτων όρων της προόδου είναι ίσο με 
Αφού η παραπάνω παράσταση είναι για κάθε
 τετράγωνο παράστασης του
τετράγωνο παράστασης του  , άρα πρέπει η διακρίνουσα
, άρα πρέπει η διακρίνουσα  να είναι μη θετική, απ΄ όπου
να είναι μη θετική, απ΄ όπου  δηλαδή
δηλαδή  .
.και τότε επιλέγουμε για τις συγκεκριμένες τιμές του

 ως παράσταση του
ως παράσταση του  την
την  .
.Αλέξανδρος
Αλέξανδρος Συγκελάκης
Re: ΕΥΚΛΕΙΔΗΣ 2016
Αν και έχω, άλλες δουλειές στο εξεταστικό κέντρο , την είδα λίγο αλλά...achilleas έγραψε:ΘΕΜΑ 2/Α ΛΥΚΕΙΟΥ
Η διακρίνουσα του τριωνύμου είναι
Παρατηρούμε ότι ο αριθμόςλήγει σε 6, όπως και ο αριθμός
.
Συνεπώς, ηλήγει σε 2. Αλλά δεν υπάρχει τέλειο τετράγωνο ακεραίου που να λήγει σε 2, οπότε η διακρίνουσα δεν είναι τέλειο τετράγωνο ακεραίου.
Συνεπώς, η εξίσωση δεν έχει ρητή ρίζα.
Φιλικά,
Αχιλλέας
Αχιλλέα
Πολύ δυνατή λύση .
Φιλικά Νίκος
Re: ΕΥΚΛΕΙΔΗΣ 2016
Μια άλλη λύση από το μαθητή μας Νίκο Ευγενίδη για το Θέμα 2 της Β Λυκείου:
Προσθέτοντας το και στα δύο μέλη παίρνουμε
και στα δύο μέλη παίρνουμε
 ,
,
Οπότε![x=\dfrac{x+2}{\sqrt[3]{11}} x=\dfrac{x+2}{\sqrt[3]{11}}](/forum/ext/geomar/texintegr/latexrender/pictures/e5857f3c418781a4807262fc7429b727.png) , κι έτσι
, κι έτσι ![x=\dfrac{2}{\sqrt[3]{11}-1} x=\dfrac{2}{\sqrt[3]{11}-1}](/forum/ext/geomar/texintegr/latexrender/pictures/67ba031c2b12ec1cb7e4edf5a4a7cde3.png) .
.
Για την αντιγραφή,
Αχιλλέας
Edit: Τυπογραφικό.
Προσθέτοντας το
 και στα δύο μέλη παίρνουμε
και στα δύο μέλη παίρνουμε ,
,Οπότε
![x=\dfrac{x+2}{\sqrt[3]{11}} x=\dfrac{x+2}{\sqrt[3]{11}}](/forum/ext/geomar/texintegr/latexrender/pictures/e5857f3c418781a4807262fc7429b727.png) , κι έτσι
, κι έτσι ![x=\dfrac{2}{\sqrt[3]{11}-1} x=\dfrac{2}{\sqrt[3]{11}-1}](/forum/ext/geomar/texintegr/latexrender/pictures/67ba031c2b12ec1cb7e4edf5a4a7cde3.png) .
.Για την αντιγραφή,
Αχιλλέας
Edit: Τυπογραφικό.
τελευταία επεξεργασία από achilleas σε Σάβ Ιαν 16, 2016 12:42 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Re: ΕΥΚΛΕΙΔΗΣ 2016
Γεωμετρία Γ
Ισοσκελή τραπέζια ...και άρα  παραλληλόγραμμο
παραλληλόγραμμο
 παραλληλόγραμμο
παραλληλόγραμμο
τελευταία επεξεργασία από KARKAR σε Σάβ Ιαν 16, 2016 7:47 pm, έχει επεξεργασθεί 1 φορά συνολικά.
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: ΕΥΚΛΕΙΔΗΣ 2016
3ο της Γ Λυκείου
(α) Για και στις δύο αρχικές σχέσεις παίρνουμε
και στις δύο αρχικές σχέσεις παίρνουμε  , για κάθε
, για κάθε  και
και  για κάθε
για κάθε  , όπου
, όπου  και
και 
Έστω . Τότε έχουμε διαδοχικά:
. Τότε έχουμε διαδοχικά:
 .
.
Άρα η είναι
είναι  . Όμοια και η
. Όμοια και η  είναι
είναι  .
.
(β) Για στην αρχική παίρνουμε
στην αρχική παίρνουμε  και επειδή η
και επειδή η  είναι
είναι  και
και  άρα
άρα  . Όμοια
. Όμοια  .
.
Άρα , για κάθε
, για κάθε  και
και  για κάθε
για κάθε  .
.
Οπότε η πρώτη σχέση γράφεται
κι επειδή η είναι
είναι  άρα
άρα  , για κάθε
, για κάθε 
Για παίρνουμε το ζητούμενο.
παίρνουμε το ζητούμενο.
Όμοια προκύπτει ότι για κάθε
για κάθε  .
.
Αλέξανδρος
(α) Για
 και στις δύο αρχικές σχέσεις παίρνουμε
και στις δύο αρχικές σχέσεις παίρνουμε  , για κάθε
, για κάθε  και
και  για κάθε
για κάθε  , όπου
, όπου  και
και 
Έστω
 . Τότε έχουμε διαδοχικά:
. Τότε έχουμε διαδοχικά: .
.Άρα η
 είναι
είναι  . Όμοια και η
. Όμοια και η  είναι
είναι  .
.(β) Για
 στην αρχική παίρνουμε
στην αρχική παίρνουμε  και επειδή η
και επειδή η  είναι
είναι  και
και  άρα
άρα  . Όμοια
. Όμοια  .
.Άρα
 , για κάθε
, για κάθε  και
και  για κάθε
για κάθε  .
.Οπότε η πρώτη σχέση γράφεται

κι επειδή η
 είναι
είναι  άρα
άρα  , για κάθε
, για κάθε 
Για
 παίρνουμε το ζητούμενο.
παίρνουμε το ζητούμενο. Όμοια προκύπτει ότι
 για κάθε
για κάθε  .
.Αλέξανδρος
Αλέξανδρος Συγκελάκης
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 13 επισκέπτες

![\displaystyle{\sqrt[3]{x} = y \Leftrightarrow x = {y^3}} \displaystyle{\sqrt[3]{x} = y \Leftrightarrow x = {y^3}}](/forum/ext/geomar/texintegr/latexrender/pictures/bd5e0e7882af8f598e5cb56885e1e84d.png) και η παράσταση γράφεται:
και η παράσταση γράφεται:


 ισούται με
ισούται με 
 και
και  .
. .
.