 ώστε
ώστε 
1) Nα βρεθεί ο τύπος της
2) Να υπολογιστεί το εμβαδό
 του χωρίου μεταξύ των
του χωρίου μεταξύ των 
3) Nα αποδείξετε οτι η εξίσωση

έχει μοναδική (αρνητική) ρίζα
 .
.4) Να βρεθεί η τιμή
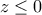 ώστε
ώστε 
Συντονιστής: Μπάμπης Στεργίου
Καλησπέρα. μια προσπάθεια...erxmer έγραψε:Δίνεται η παραγωγίσιμη συνάρτησηώστε
1) Nα βρεθεί ο τύπος της
2) Να υπολογιστεί το εμβαδότου χωρίου μεταξύ των
3) Nα αποδείξετε οτι η εξίσωση
έχει μοναδική (αρνητική) ρίζα.
4) Να βρεθεί η τιμήώστε






 (1)
(1) και προκύπτει
και προκύπτει  .
.


 ώστε
ώστε  . ΑΤΟΠΟ.
. ΑΤΟΠΟ. , για κάθε
, για κάθε  .
. οπότε
οπότε  .
. . Έχουμε απροσδιόριστη μορφή
. Έχουμε απροσδιόριστη μορφή  .
. .
. ,
, είναι
είναι 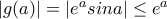


 , από κριτήριο Παρεμβολής είναι
, από κριτήριο Παρεμβολής είναι  .
.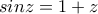 .
.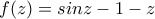 , παραγωγίσιμη με
, παραγωγίσιμη με 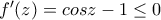 .
. μηδενίζεται για μεμονωμένες τιμές :
μηδενίζεται για μεμονωμένες τιμές :  και εφ΄όσον
και εφ΄όσον  συνεχής ,
συνεχής ,  είναι γνησίως φθίνουσα , άρα και 1-1.
είναι γνησίως φθίνουσα , άρα και 1-1.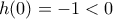 ,
,  , ισχύουν οι προϋποθέσεις του Θ. Bolzano στο
, ισχύουν οι προϋποθέσεις του Θ. Bolzano στο ![[-2\pi , 0] [-2\pi , 0]](/forum/ext/geomar/texintegr/latexrender/pictures/70b7ae9eb36512831ddf32e3b9486989.png) .
.  στο
στο 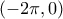 και αφού η
και αφού η  είναι 1-1 στο
είναι 1-1 στο  , είναι μοναδική .
, είναι μοναδική . ) προκύπτει :
) προκύπτει :  .
.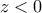 δεν υπάρχει το
δεν υπάρχει το  , διότι προκύπτει
, διότι προκύπτει  από αριστερά
από αριστερά  από δεξιά.
από δεξιά. έχουμε
έχουμε 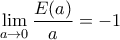 .
. .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες