 για την οποία ισχύει:
για την οποία ισχύει: 
1) Nα βρεθεί τύπος της συνάρτησης
2) Να δικαιολογήσετε ότι η
 αντιστρέφεται και να βρείτε το πεδίο ορισμού της αντίστροφης
αντιστρέφεται και να βρείτε το πεδίο ορισμού της αντίστροφης3) Να βρείτε το εμβαδόν του χωρίου που περικλείεται από την
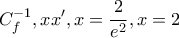 , με την
, με την  να είναι συνεχής συνάρτηση στο πεδίο ορισμού της.
να είναι συνεχής συνάρτηση στο πεδίο ορισμού της.4) Να δείξετε ότι η εξίσωση
 έχει ακριβώς μια ρίζα στο
έχει ακριβώς μια ρίζα στο 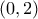
5)
 και
και ![\displaystyle{\lim_{x \to 0^{-}}\left [ f(x) \right ]^\displaystyle{\frac{e^{x^2}}{sin^3x}}} \displaystyle{\lim_{x \to 0^{-}}\left [ f(x) \right ]^\displaystyle{\frac{e^{x^2}}{sin^3x}}}](/forum/ext/geomar/texintegr/latexrender/pictures/111718d17ef1f4d2a05a03f367864b1b.png)

 και έχουμε:
και έχουμε: 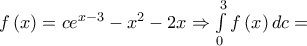

![c - 20 = \left[ {c{e^{x - 3}} - \dfrac{{{x^3}}}{3} - {x^2}} \right]_0^3 \Rightarrow c - 20 = \left[ {c{e^{x - 3}} - \dfrac{{{x^3}}}{3} - {x^2}} \right]_0^3 \Rightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/d2dadcd9a81dbec4ad607d29b74e4fca.png)

 .
. , με
, με 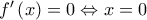 (αφού αν
(αφού αν  είναι γνωστή πρόταση (προκύπτει από την κυρτότητα της
είναι γνωστή πρόταση (προκύπτει από την κυρτότητα της  ότι η γραφική της παράσταση είναι «πάνω» από την εφαπτόμενή της σε κάθε σημείο της (άρα και στο
ότι η γραφική της παράσταση είναι «πάνω» από την εφαπτόμενή της σε κάθε σημείο της (άρα και στο  ) που είναι η ευθεία
) που είναι η ευθεία  εκτός του σημείου επαφής)
εκτός του σημείου επαφής) είναι
είναι 
![\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to - \infty } \left[ {2{e^x} - {x^2} - 2x} \right] = \mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to - \infty } \left[ {2{e^x} - {x^2} - 2x} \right] =](/forum/ext/geomar/texintegr/latexrender/pictures/337319f03ccf89a3f15b439d8db301f6.png)
![\mathop {\lim }\limits_{x \to - \infty } \left[ {2{e^x} - \left( {{x^2} + 2x} \right)} \right]\mathop = \limits^{\mathop {\lim }\limits_{x \to - \infty } \left( {2{e^x}} \right) = 0,\mathop {\lim }\limits_{x \to - \infty } \left( {{x^2} + 2x} \right) = + \infty } \ldots - \infty \mathop {\lim }\limits_{x \to - \infty } \left[ {2{e^x} - \left( {{x^2} + 2x} \right)} \right]\mathop = \limits^{\mathop {\lim }\limits_{x \to - \infty } \left( {2{e^x}} \right) = 0,\mathop {\lim }\limits_{x \to - \infty } \left( {{x^2} + 2x} \right) = + \infty } \ldots - \infty](/forum/ext/geomar/texintegr/latexrender/pictures/4195bb33d15e0f862cc7c77309be6304.png)
![\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ {2{e^x} - {x^2} - 2x} \right] = \mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ {2{e^x} - {x^2} - 2x} \right] =](/forum/ext/geomar/texintegr/latexrender/pictures/070385d729df4cb35e0d63c97c8ce518.png)
![\mathop {\lim }\limits_{x \to + \infty } \left[ {{e^x}\left( {2 - \dfrac{{{x^2}}}{{{e^x}}} - \dfrac{{2x}}{{{e^x}}}} \right)} \right] = \ldots + \infty \mathop {\lim }\limits_{x \to + \infty } \left[ {{e^x}\left( {2 - \dfrac{{{x^2}}}{{{e^x}}} - \dfrac{{2x}}{{{e^x}}}} \right)} \right] = \ldots + \infty](/forum/ext/geomar/texintegr/latexrender/pictures/da3f47febd2ee3d29ed793b61c60e589.png) .
. 
 )
)
 προκύπτει άμεσα από το γεγονός της συμμετρίας της συνεχούς συνάρτησης
προκύπτει άμεσα από το γεγονός της συμμετρίας της συνεχούς συνάρτησης 

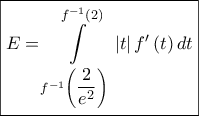 .
. και
και  , άρα
, άρα
![\left[ {tf\left( t \right)} \right]_0^{ - 2} - \int\limits_0^{ - 2} {f\left( t \right)dt} = \left[ {tf\left( t \right)} \right]_0^{ - 2} - \int\limits_0^{ - 2} {f\left( t \right)dt} =](/forum/ext/geomar/texintegr/latexrender/pictures/9962b2a65f38479e96acd020f2884750.png)

![= \dfrac{2}{{{e^2}}} - \left[ {2{e^t} - \dfrac{{{t^3}}}{3} - {t^2}} \right]_0^{ - 2} = = \dfrac{2}{{{e^2}}} - \left[ {2{e^t} - \dfrac{{{t^3}}}{3} - {t^2}} \right]_0^{ - 2} =](/forum/ext/geomar/texintegr/latexrender/pictures/681120ab65b6a0d032e2db6a5c4edb80.png)
 .
.
![\left[ {0,2} \right] \left[ {0,2} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/5d94ae192de6d9e3eaf6db503901620f.png) (πράξεις με συνεχείς) με
(πράξεις με συνεχείς) με  και
και  οπότε
οπότε 

 και
και 
![\mathop \Rightarrow \limits^{f\left( {3t} \right) \ne f\left( 0 \right),\forall t \in \left( {0,2} \right]} \mathop \Rightarrow \limits^{f\left( {3t} \right) \ne f\left( 0 \right),\forall t \in \left( {0,2} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/b955e315b1270f90e817b9b955ec3439.png)

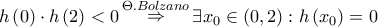
 (πράξεις με παραγωγίσιμες)
(πράξεις με παραγωγίσιμες)
![= 8 + \int\limits_0^2 {\left[ {f\left( {\dfrac{t}{2}} \right) - 2f\left( {3t} \right)} \right]dt} = = 8 + \int\limits_0^2 {\left[ {f\left( {\dfrac{t}{2}} \right) - 2f\left( {3t} \right)} \right]dt} =](/forum/ext/geomar/texintegr/latexrender/pictures/7c3068e5b9c18192c59e1aa0d553fc36.png)
![8 + \int\limits_0^2 {\left[ {2{e^{\dfrac{t}{2}}} - \dfrac{{{t^2}}}{4} - t - 4{e^{3t}} + 18{t^2} + 12t} \right]dt} = 8 + \int\limits_0^2 {\left[ {2{e^{\dfrac{t}{2}}} - \dfrac{{{t^2}}}{4} - t - 4{e^{3t}} + 18{t^2} + 12t} \right]dt} =](/forum/ext/geomar/texintegr/latexrender/pictures/ef2f62100b4a9bc3fb8454495145e404.png)
![8 + \left[ {4{e^{\dfrac{t}{2}}} - \dfrac{{{t^3}}}{{12}} - \dfrac{{{t^2}}}{2} - 4\dfrac{{{e^{3t}}}}{3} + 6{t^3} + 6{t^2}} \right]_0^2 8 + \left[ {4{e^{\dfrac{t}{2}}} - \dfrac{{{t^3}}}{{12}} - \dfrac{{{t^2}}}{2} - 4\dfrac{{{e^{3t}}}}{3} + 6{t^3} + 6{t^2}} \right]_0^2](/forum/ext/geomar/texintegr/latexrender/pictures/00950ead481b6f699c127b7854b33368.png)

 γνησίως φθίνουσα στο
γνησίως φθίνουσα στο  οπότε η εξίσωση
οπότε η εξίσωση 
 έχει μοναδική ρίζα.
έχει μοναδική ρίζα.


![\mathop {\lim }\limits_{x \to + \infty } \left[ {\dfrac{1}{2}\dfrac{{\dfrac{{f'\left( x \right)}}{{f\left( x \right)}}}}{{\dfrac{1}{{2x\sqrt {\ln x} }}}}} \right] = \mathop {\lim }\limits_{x \to + \infty } \left[ {\dfrac{{xf'\left( x \right)}}{{f\left( x \right)}} \cdot \sqrt {\ln x} } \right] \mathop {\lim }\limits_{x \to + \infty } \left[ {\dfrac{1}{2}\dfrac{{\dfrac{{f'\left( x \right)}}{{f\left( x \right)}}}}{{\dfrac{1}{{2x\sqrt {\ln x} }}}}} \right] = \mathop {\lim }\limits_{x \to + \infty } \left[ {\dfrac{{xf'\left( x \right)}}{{f\left( x \right)}} \cdot \sqrt {\ln x} } \right]](/forum/ext/geomar/texintegr/latexrender/pictures/438625a849e4c44a82c87551aba35844.png)

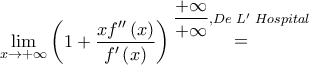





 και
και![\mathop {\lim }\limits_{x \to {0^ - }} {\left[ {f\left( x \right)} \right]^{\dfrac{{{e^{{x^2}}}}}{{{{\sin }^3}x}}}} = \mathop {\lim }\limits_{x \to {0^ - }} {e^{^{\dfrac{{{e^{{x^2}}}}}{{{{\sin }^3}x}}\ln f\left( x \right)}}} \mathop {\lim }\limits_{x \to {0^ - }} {\left[ {f\left( x \right)} \right]^{\dfrac{{{e^{{x^2}}}}}{{{{\sin }^3}x}}}} = \mathop {\lim }\limits_{x \to {0^ - }} {e^{^{\dfrac{{{e^{{x^2}}}}}{{{{\sin }^3}x}}\ln f\left( x \right)}}}](/forum/ext/geomar/texintegr/latexrender/pictures/46461e16a14d1bbc840a7befd8d91dbf.png) .
. και είναι
και είναι  και
και 

![\boxed{\mathop {\lim }\limits_{x \to {0^ - }} {{\left[ {f\left( x \right)} \right]}^{\dfrac{{{e^{{x^2}}}}}{{{{\sin }^3}x}}}} = 0} \boxed{\mathop {\lim }\limits_{x \to {0^ - }} {{\left[ {f\left( x \right)} \right]}^{\dfrac{{{e^{{x^2}}}}}{{{{\sin }^3}x}}}} = 0}](/forum/ext/geomar/texintegr/latexrender/pictures/3b7d67b8901bcf7a6c7f00b5605ae320.png)