erxmer έγραψε:Δίνεται η παραγωγίσιμη

, με σύνολο τιμών το

και η συνάρτηση

ώστε:

1) Nα μελετηθεί η

ως προς την μονοτονία και τη κυρτότητα
2) Να μελετηθεί η

ως προς την συνέχεια στο σημείο
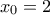
3) Nα αποδείξετε οτι η

αντιστρέφεται και να βρείτε τον τύπο της αντίστροφης
4) Αν

, να βρεθεί η ασύμπτωτη της

στο

5) Nα αποδείξετε οτι
 ***διορθώση δεδομένων***
***διορθώση δεδομένων***
...Καλησπέρα

μια αντιμετώπιση μέχρι το (4)....
1) Παραγωγίζοντας την σχέση

έχουμε ότι

άρα
η

είναι γνήσια αύξουσα στο

και παραγωγίζοντας την
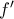
έχουμε ότι

(1)
Τώρα για το πρόσημο της

αν στην σχέση

για όπου

το

προκύπτει ότι
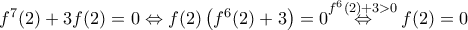
δηλαδή το

ρίζα της

που είναι και μοναδική αφού

είναι γνήσια αύξουσα στο

άρα και
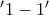
και ακόμη για

επομένως λόγω (1) και

επομένως η

είναι κοίλη στο

και ακόμη για

επομένως λόγω (1) και

επομένως η

είναι κοίλη στο
![(-\infty ,\,2] (-\infty ,\,2]](/forum/ext/geomar/texintegr/latexrender/pictures/500bfd3d63b20733175f16c9e420cacb.png)
2) Αν

τότε

δηλαδή η

είναι γνήσια αύξουσα στο

και από την σχέση

προκύπτει ότι

και επειδή για

η

είναι γνήσια αύξουσα στο

.
Τώρα για


και ανάλογα για


άρα ισχύει ότι

επομένως και

και αφού

από κριτήριο παρεμβολής έχουμε ότι

άρα η

συνεχής στο

3) Επειδή η

είναι γνήσια αύξουσα στο

άρα και
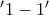
αντιστρέφεται με

αφού σύνολο τιμών της

είναι τι

από υπόθεση και έτσι με όπου

το

στην σχέση

προκύπτει ότι

4) Είναι

άρα και

στο

και ακόμη
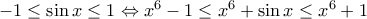
άρα


επομένως για

ισχύει ότι

και επειδή

από κριτήριο παρεμβολής ισχύει ότι

Τώρα
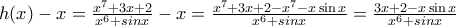

και επειδή

(….με κριτήριο παρεμβολής ) προκύπτει ότι
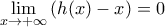
επομένως η ευθεία

είναι ασύμπτωτη της

στο

.
...τώρα

...
Φιλικά και Μαθηματικά
Βασίλης
 , με σύνολο τιμών το
, με σύνολο τιμών το  και η συνάρτηση
και η συνάρτηση  ώστε:
ώστε:
 ως προς την μονοτονία και τη κυρτότητα
ως προς την μονοτονία και τη κυρτότητα ως προς την συνέχεια στο σημείο
ως προς την συνέχεια στο σημείο 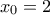
 αντιστρέφεται και να βρείτε τον τύπο της αντίστροφης
αντιστρέφεται και να βρείτε τον τύπο της αντίστροφης , να βρεθεί η ασύμπτωτη της
, να βρεθεί η ασύμπτωτη της  στο
στο 


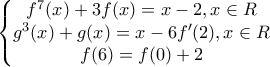
 Δεν ισχύει.Γιατί
Δεν ισχύει.Γιατί 


 ΑΤΟΠΟ (θα είχαμε
ΑΤΟΠΟ (θα είχαμε  )
) έχουμε ότι
έχουμε ότι  άρα
άρα 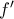 έχουμε ότι
έχουμε ότι  (1)
(1) το
το  προκύπτει ότι
προκύπτει ότι 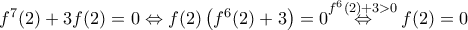
 ρίζα της
ρίζα της 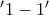 και ακόμη για
και ακόμη για  επομένως λόγω (1) και
επομένως λόγω (1) και  επομένως η
επομένως η 
 επομένως λόγω (1) και
επομένως λόγω (1) και  επομένως η
επομένως η ![(-\infty ,\,2] (-\infty ,\,2]](/forum/ext/geomar/texintegr/latexrender/pictures/500bfd3d63b20733175f16c9e420cacb.png)
 τότε
τότε  δηλαδή η
δηλαδή η  είναι γνήσια αύξουσα στο
είναι γνήσια αύξουσα στο  προκύπτει ότι
προκύπτει ότι  και επειδή για
και επειδή για  η
η 
 και ανάλογα για
και ανάλογα για 
 άρα ισχύει ότι
άρα ισχύει ότι  επομένως και
επομένως και  και αφού
και αφού 
 άρα η
άρα η  αφού σύνολο τιμών της
αφού σύνολο τιμών της  στην σχέση
στην σχέση 
 άρα και
άρα και  στο
στο 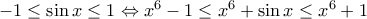 άρα
άρα 
 επομένως για
επομένως για  και επειδή
και επειδή 

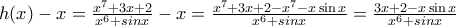
 και επειδή
και επειδή  (….με κριτήριο παρεμβολής ) προκύπτει ότι
(….με κριτήριο παρεμβολής ) προκύπτει ότι 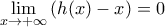 επομένως η ευθεία
επομένως η ευθεία  είναι ασύμπτωτη της
είναι ασύμπτωτη της ![[2,a] [2,a]](/forum/ext/geomar/texintegr/latexrender/pictures/92896db73967e3fdd84d7dd03f5630a5.png) λαμβάνουμε ότι:
λαμβάνουμε ότι:

![[a,a+2] [a,a+2]](/forum/ext/geomar/texintegr/latexrender/pictures/f0d3eef5a25d5504129c88b25a4ec527.png) λαμβάνουμε ότι:
λαμβάνουμε ότι:

 γνησίως φθίνουσα
γνησίως φθίνουσα 






 )
)