 παραγωγίσιμη στο
παραγωγίσιμη στο ![[1, 2] [1, 2]](/forum/ext/geomar/texintegr/latexrender/pictures/04cd0e0151f352e7fd414d694a604136.png) με
με  και
και  για κάθε
για κάθε ![x\in[1, 2]. x\in[1, 2].](/forum/ext/geomar/texintegr/latexrender/pictures/3c0ce9c692ebb159ea923d88653f2431.png)
Να δείξετε ότι

Συντονιστής: Καρδαμίτσης Σπύρος
 παραγωγίσιμη στο
παραγωγίσιμη στο ![[1, 2] [1, 2]](/forum/ext/geomar/texintegr/latexrender/pictures/04cd0e0151f352e7fd414d694a604136.png) με
με  και
και  για κάθε
για κάθε ![x\in[1, 2]. x\in[1, 2].](/forum/ext/geomar/texintegr/latexrender/pictures/3c0ce9c692ebb159ea923d88653f2431.png)

![\displaystyle f'\left( x \right) + f\left( x \right) > 1 \Leftrightarrow {e^x}f'\left( x \right) + {e^x}f\left( x \right) - {e^x} > 0,x \in \left[ {1,2} \right] \displaystyle f'\left( x \right) + f\left( x \right) > 1 \Leftrightarrow {e^x}f'\left( x \right) + {e^x}f\left( x \right) - {e^x} > 0,x \in \left[ {1,2} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/87a5a288a1a8e9325183df5582626024.png)
![\displaystyle h\left( x \right) = {e^x}f\left( x \right) - {e^x},x \in \left[ {1,2} \right] \displaystyle h\left( x \right) = {e^x}f\left( x \right) - {e^x},x \in \left[ {1,2} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/e6623a717bc027987995bbb33f910f61.png) που είναι παραγωγίσιμη συνάρτηση και γνωρίζοντας ότι
που είναι παραγωγίσιμη συνάρτηση και γνωρίζοντας ότι  στο
στο  , συμπεραίνουμε ότι η
, συμπεραίνουμε ότι η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο ![\displaystyle \left[ {1,2} \right] \displaystyle \left[ {1,2} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/be1a9041ee52859edb2dd45666890581.png) .
.


 είναι γνήσια αύξουσα στο διάστημα
είναι γνήσια αύξουσα στο διάστημα ![[1, 2] [1, 2]](/forum/ext/geomar/texintegr/latexrender/pictures/04cd0e0151f352e7fd414d694a604136.png) . Τότε όμως
. Τότε όμως 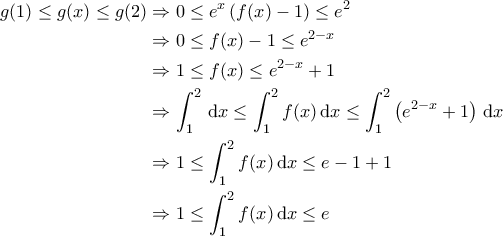

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες