 .
.1) Nα βρεθεί το σύνολο τιμών της
2) Να βρεθεί το πλήθος των θετικών ριζών της εξίσωσης

3) Αν
 δείξτε οτι
δείξτε οτι  και να βρεθεί το
και να βρεθεί το 
4) Nα υπολογιστεί το
 και
και 
Συντονιστής: Καρδαμίτσης Σπύρος
Καλησπέρα. Μια προσπάθεια στην, πραγματικά, καλή...erxmer έγραψε:Δίνεται η συνάρτηση με τύπο.
1) Nα βρεθεί το σύνολο τιμών της
2) Να βρεθεί το πλήθος των θετικών ριζών της εξίσωσης
3) Ανδείξτε οτι
και να βρεθεί το
4) Nα υπολογιστεί τοκαι

 έχουμε
έχουμε 
 έχουμε
έχουμε 
 έχουμε
έχουμε 
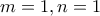 έχουμε
έχουμε 
 άρτιο, από την (α),(β) έχουμε :
άρτιο, από την (α),(β) έχουμε : 


 ή
ή  .
.


 \displaystyle{x\in \left ( 0,e^{-\frac{m}{n}} \right )\cup \left ( 1 ,+\infty \right )
\displaystyle{x\in \left ( 0,e^{-\frac{m}{n}} \right )\cup \left ( 1 ,+\infty \right ) f'(x)<0
f'(x)<0 \Leftrightarrow
\Leftrightarrow x^{n-1}(lnx)^{m-1}lnx(nlnx+m)<0
x^{n-1}(lnx)^{m-1}lnx(nlnx+m)<0 \Leftrightarrow}
\Leftrightarrow} .
.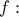 γνησίως αύξουσα στο
γνησίως αύξουσα στο ![\left ( 0,e^{-\frac{m}{n}} \right ] \left ( 0,e^{-\frac{m}{n}} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/a4ad83a3b3da044006042f3ad3ad22e6.png) ,
,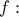 γνησίως φθίνουσα στο
γνησίως φθίνουσα στο ![\left [e^{-\frac{m}{n}},1 \right ] \left [e^{-\frac{m}{n}},1 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/b12762b43c7c283a51c17c6f850a53dc.png) και
και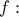 γνησίως αύξουσα στο
γνησίως αύξουσα στο  .
. . (Απροσδιόριστη μορφή
. (Απροσδιόριστη μορφή  , κανόνας de L' Hospital).
, κανόνας de L' Hospital).

 και
και 

 περιττό, από την (α),(γ) και (δ) έχουμε :
περιττό, από την (α),(γ) και (δ) έχουμε : 


 ή
ή  .
.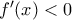


 \displaystyle{x\in \left ( 0,e^{-\frac{m}{n}} \right )
\displaystyle{x\in \left ( 0,e^{-\frac{m}{n}} \right ) f'(x)>0
f'(x)>0 \Leftrightarrow
\Leftrightarrow x^{n-1}(lnx)^{m-1}lnx(nlnx+m)>0
x^{n-1}(lnx)^{m-1}lnx(nlnx+m)>0 \Leftrightarrow}
\Leftrightarrow} .
.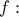 γνησίως φθίνουσα στο
γνησίως φθίνουσα στο ![\left ( 0,e^{-\frac{m}{n}} \right ] \left ( 0,e^{-\frac{m}{n}} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/a4ad83a3b3da044006042f3ad3ad22e6.png) ,
,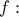 γνησίως αύξουσα στο
γνησίως αύξουσα στο  , αφού είναι συνεχής.
, αφού είναι συνεχής.
 .
. με
με  , από όπου με πινακάκι κατά τα γνωστά προκύπτει:
, από όπου με πινακάκι κατά τα γνωστά προκύπτει:
 . Άρα
. Άρα  γνησίως φθίνουσα στο
γνησίως φθίνουσα στο ![\left (0, e^{-\frac{1}{n}} \right ]. \left (0, e^{-\frac{1}{n}} \right ].](/forum/ext/geomar/texintegr/latexrender/pictures/32e7a3643514785b71df313296756bb5.png)

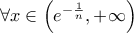 . Άρα
. Άρα  γνησίως αύξουσα στο
γνησίως αύξουσα στο 
 παρουσιάζει ολικό ελάχιστο το:
παρουσιάζει ολικό ελάχιστο το: 
 , η εξίσωση έχει μοναδική λύση την
, η εξίσωση έχει μοναδική λύση την  .
. , η εξίσωση έχει 2 λύσεις , μία στο
, η εξίσωση έχει 2 λύσεις , μία στο  και την άλλη στο
και την άλλη στο  ,
,


 .
.
 όπως απεδείχθη προηγουμένως και
όπως απεδείχθη προηγουμένως και 
 .
. .
. .
. .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες