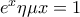 βρίσκεται ρίζα της εξίσωσης
βρίσκεται ρίζα της εξίσωσης  .
.Συντονιστής: Καρδαμίτσης Σπύρος
Καλησπέρα ! Μια προσπάθεια μόνο με Θεώρημα Bolzano...Πρωτοπαπάς Λευτέρης έγραψε:Να αποδείξετε ότι ανάμεσα σε δύο ρίζες της εξίσωσηςβρίσκεται ρίζα της εξίσωσης
.
 .
.  στο
στο ![\left [ 0, \dfrac{\pi }{2} \right ] \left [ 0, \dfrac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/6d1d0841b1435e89d1dda86690990416.png) .
.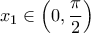 τέτοιο ώστε
τέτοιο ώστε 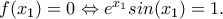
 στο
στο ![\left [ \dfrac{\pi }{2} , \pi \right ] \left [ \dfrac{\pi }{2} , \pi \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/52364ea35f4c575fe81a98c0b64c8805.png) .
. τέτοιο ώστε
τέτοιο ώστε 
 .
. 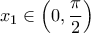

 . Άρα
. Άρα 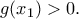
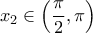

 . Άρα
. Άρα 
 στο
στο ![\left [ x_{1} , x_{2} \right ] \left [ x_{1} , x_{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/2bea437b21fb801dd95d500ff3b47f36.png) , προκύπτει το ζητούμενο.
, προκύπτει το ζητούμενο.Λευτέρη, μήπως εννοείς να σχεδιάσουμε τηςΠρωτοπαπάς Λευτέρης έγραψε:Καλησπέρα.
Μια χαρά λύση είναι αυτή.
Για τη συγκεκριμένη έχω λύση χωρίς Rolle, χωρίς χρήση παραγωγισιμότητας ...
Δεν την ανεβάζω ακόμα.
 και να φανούν όλα ξεκάθαρα ; Κοιτάζοντας τα διαστήματα που οι δύο τριγωνομετρικές συναρτήσεις είναι θετικές, η συνέχεια και των τριών εξασφαλίζει ότι οι φαινομενικές τομές είναι ...τομές .
και να φανούν όλα ξεκάθαρα ; Κοιτάζοντας τα διαστήματα που οι δύο τριγωνομετρικές συναρτήσεις είναι θετικές, η συνέχεια και των τριών εξασφαλίζει ότι οι φαινομενικές τομές είναι ...τομές .Γεια σου Σταμάτη.Σταμ. Γλάρος έγραψε:
Θεωρώ, τώρα, την συνάρτηση.
Επειδή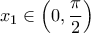

. Άρα
Φιλικά
Σταμ. Γλάρος

Μπάμπη καλή Σαρακοστή.Μπάμπης Στεργίου έγραψε:Λευτέρη, μήπως εννοείς να σχεδιάσουμε τηςΠρωτοπαπάς Λευτέρης έγραψε:Καλησπέρα.
Μια χαρά λύση είναι αυτή.
Για τη συγκεκριμένη έχω λύση χωρίς Rolle, χωρίς χρήση παραγωγισιμότητας ...
Δεν την ανεβάζω ακόμα.και να φανούν όλα ξεκάθαρα ; Κοιτάζοντας τα διαστήματα που οι δύο τριγωνομετρικές συναρτήσεις είναι θετικές, η συνέχεια και των τριών εξασφαλίζει ότι οι φαινομενικές τομές είναι ...τομές .
Καλό βράδυ και καλή Σαρακοστή !
Καλησπέρα σε όλους.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:Γεια σου Σταμάτη.Σταμ. Γλάρος έγραψε:
Θεωρώ, τώρα, την συνάρτηση.
Επειδή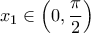

. Άρα
Φιλικά
Σταμ. Γλάρος
Αυτό που απομόνωσα παραπάνω δεν είναι ακριβές.
π.χ αν σπάσει ο διάολος το ποδάρι του και είναι
δεν ισχύει.
Καλησπέρα.Σταμ. Γλάρος έγραψε:Καλησπέρα ! Μια προσπάθεια μόνο με Θεώρημα Bolzano...Πρωτοπαπάς Λευτέρης έγραψε:Να αποδείξετε ότι ανάμεσα σε δύο ρίζες της εξίσωσηςβρίσκεται ρίζα της εξίσωσης
.
Θεωρώ την συνάρτηση.
Ισχύουν οι προϋποθέσεις του Θεωρήματος Bolzano για τηνστο
.
Συνεπώς υπάρχει τουλάχιστον ένατέτοιο ώστε
Επίσης ισχύουν οι προϋποθέσεις του Θεωρήματος Bolzano για τηνστο
.
Συνεπώς υπάρχει τουλάχιστον ένατέτοιο ώστε
Θεωρώ, τώρα, την συνάρτηση.
Επειδή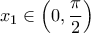

. Άρα
Ομοίως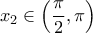

. Άρα
Συνεπώς από Θεώρημα Bolzano για τηνστο
, προκύπτει το ζητούμενο.
Φιλικά
Σταμ. Γλάρος
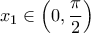

 . Άρα
. Άρα 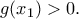 " υπάρχει πρόβλημα.
" υπάρχει πρόβλημα.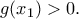 Για αυτό περιορίζω το διάστημα στο οποίο ανήκει η
Για αυτό περιορίζω το διάστημα στο οποίο ανήκει η 
 και
και 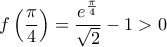
 , το οποίο ισχύει επειδή
, το οποίο ισχύει επειδή  .
.  στο
στο ![\left [ 0, \dfrac{\pi }{4} \right ] \left [ 0, \dfrac{\pi }{4} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/b588561d8e618a906a6f89e009f45b7a.png) , υπάρχει τουλάχιστον ένα
, υπάρχει τουλάχιστον ένα  τέτοιο ώστε
τέτοιο ώστε 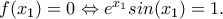
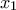 είναι μοναδική στο διάστημα αυτό αφού η
είναι μοναδική στο διάστημα αυτό αφού η  είναι γνησίως αύξουσα στο πρώτο τεταρτημόριο.
είναι γνησίως αύξουσα στο πρώτο τεταρτημόριο. ισοδυνάμως έχουμε :
ισοδυνάμως έχουμε : (1)
(1) (2)
(2)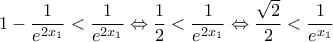 .
.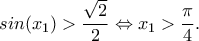 Άτοπο.
Άτοπο. και νομίζω ότι η .... τρύπα έκλεισε !
και νομίζω ότι η .... τρύπα έκλεισε ! .
. με
με 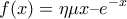 όπου
όπου  .
. έχουμε ότι
έχουμε ότι 
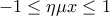 ,
, για κάθε
για κάθε  .
. είναι αδύνατη όταν
είναι αδύνατη όταν  .
. .
. .
. ,
, ,
,
 ,
, .
. ικανοποιεί τις προϋποθέσεις του Θ.Bolzano στο
ικανοποιεί τις προϋποθέσεις του Θ.Bolzano στο ![\displaystyle{\left[ 2k\pi, 2k\pi +\frac{\pi}{4} \right]} \displaystyle{\left[ 2k\pi, 2k\pi +\frac{\pi}{4} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/537c0fce35166640c6241a0e2e4fa11a.png) , άρα υπάρχει
, άρα υπάρχει  ώστε
ώστε  .
. ,
, ικανοποιεί τις προϋποθέσεις του Θ.Bolzano στο
ικανοποιεί τις προϋποθέσεις του Θ.Bolzano στο ![\displaystyle{\left[ 2k\pi+\frac{\pi}{4}, 2k\pi +\frac{5\pi}{4} \right]} \displaystyle{\left[ 2k\pi+\frac{\pi}{4}, 2k\pi +\frac{5\pi}{4} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/4e5ea56b29fb7babdd448b000f1d62b0.png) , άρα υπάρχει
, άρα υπάρχει  ώστε
ώστε  .
. .
. με
με  .
. , αφού
, αφού  και
και , αφού
, αφού 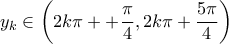 .
. ικανοποιεί τις προϋποθέσεις του Θ.Bolzano στο
ικανοποιεί τις προϋποθέσεις του Θ.Bolzano στο ![\displaystyle{[x_k,y_k]} \displaystyle{[x_k,y_k]}](/forum/ext/geomar/texintegr/latexrender/pictures/c6c77dd8cf52d9956ae4a03e5f4393bd.png) , άρα υπάρχει
, άρα υπάρχει  ώστε
ώστε  .
.Πρωτοπαπάς Λευτέρης έγραψε:Η λύση μου…
Έχουμε ότι:.
Θεωρώ τη συνάρτησημε
όπου
.
1η περίπτωση
Ανέχουμε ότι
και αφού,
έχουμε ότιγια κάθε
.
Συνεπώς η εξίσωσηείναι αδύνατη όταν
.
2η περίπτωση
Αν.
Θεωρούμε.
Τότε:
,
,
αφού
,
το οποίο ισχύει αφού.
Επομένως ηικανοποιεί τις προϋποθέσεις του Θ.Bolzano στο
, άρα υπάρχει
ώστε
.
Επίσης
,
οπότε ηικανοποιεί τις προϋποθέσεις του Θ.Bolzano στο
, άρα υπάρχει
ώστε
.
Όμως:.
Θεωρούμε τη συνάρτησημε
.
Τότε:
, αφού
και
, αφού
.
Επομένως ηικανοποιεί τις προϋποθέσεις του Θ.Bolzano στο
, άρα υπάρχει
ώστε
.
 που προκύπτουν από Bolzano είναι μοναδικές
που προκύπτουν από Bolzano είναι μοναδικές![[2k\pi +\frac{5\pi }{4},2(k+1)\pi ] [2k\pi +\frac{5\pi }{4},2(k+1)\pi ]](/forum/ext/geomar/texintegr/latexrender/pictures/bb76a24d89b4f141294a3354bc046bcf.png) η
η  δεν έχει ρίζα
δεν έχει ρίζα 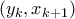 η
η  έχει ρίζα.
έχει ρίζα.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης