erxmer έγραψε:Έστω η παραγωγίσιμη συνάρτηση

για την οποία ισχύουν:

1. Δείξτε ότι η

έχει μοναδικό σημείο καμπής και προσδιορίστε τα διαστήματα στα οποία η

είναι κυρτή ή κοίλη.
2. Βρείτε τον τύπο της

.
3. Υπολογίστε το εμβαδόν του χωρίου που περικλείεται από την

, την διχοτόμο του πρώτου τεταρτημόριου και τις ευθείες

.
(α) Εφόσον ισχύει η σχέση

συμπεραίνουμε ότι η

είναι δύο φορές παραγωγίσιμη. Παραγωγίζοντας βγάζουμε

Ο παρανομαστής είναι τετριμμένα θετικός ενώ ο αριθμητής μηδενίζει στο

. Τώρα

διότι από τη δοσμένη σχέση έχουμε

δηλ. η

είναι γνήσια αύξουσα. Συνεπώς για

είναι
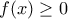
ενώ για

είναι

. Κατά συνέπεια η

έχει σημείο καμπής στο

, είναι κυρτή στο
![(-\infty, 0] (-\infty, 0]](/forum/ext/geomar/texintegr/latexrender/pictures/8bb8e3006289394bd593c5b7a4904dd6.png)
και κοίλη στο

.
(β) Έχουμε διαδοχικά:

διότι η ποσότητα

είναι αρνητική για κάθε

.
(γ) Στο
![[0, 1] [0, 1]](/forum/ext/geomar/texintegr/latexrender/pictures/264884439b70ab09a86bc848421c6de6.png)
η συνάρτησή μας είναι μεγάλυτερη ή ίση του

. Οπότε το εμβαδόν που περικλείεται της γραφικής παράστασης της

, του άξονα

και των ευθειών

και

είναι ίσο με
![\displaystyle{\begin{aligned}
{\rm E}\left ( \Omega \right ) &= \int_{0}^{1} \ln \left ( x + \sqrt{x^2+1} \right ) \, {\rm d}x \\
&= \left [ x \ln \left ( x + \sqrt{x^2+1} \right ) \right ]_0^1 - \int_{0}^{1} \frac{x}{\sqrt{x^2+1}} \, {\rm d}x \\
&= \ln \left ( 1+\sqrt{2} \right ) - \left [ \sqrt{x^2+1} \right ]_0^1 \\
&= \ln \left ( 1+\sqrt{2} \right ) - \sqrt{2} +1 \\
&= 1 - \sqrt{2} + \ln \left ( 1+\sqrt{2} \right ) \approx 0.46716
\end{aligned}} \displaystyle{\begin{aligned}
{\rm E}\left ( \Omega \right ) &= \int_{0}^{1} \ln \left ( x + \sqrt{x^2+1} \right ) \, {\rm d}x \\
&= \left [ x \ln \left ( x + \sqrt{x^2+1} \right ) \right ]_0^1 - \int_{0}^{1} \frac{x}{\sqrt{x^2+1}} \, {\rm d}x \\
&= \ln \left ( 1+\sqrt{2} \right ) - \left [ \sqrt{x^2+1} \right ]_0^1 \\
&= \ln \left ( 1+\sqrt{2} \right ) - \sqrt{2} +1 \\
&= 1 - \sqrt{2} + \ln \left ( 1+\sqrt{2} \right ) \approx 0.46716
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/bcba5ec8faea3465262d8619db96cee6.png) Edit: Φεβρουάριος 17, 2017
Edit: Φεβρουάριος 17, 2017
Το τελευταίο ερώτημα δε ζητάει αυτό που υπολόγισα. Ζητάει κάτι άλλο. Η συνάρτηση

είναι κοίλη στο

και η εφαπτομένη στο σημείο

είναι η ευθεία

. Κατά συνέπεια η εφαπτομένη θα είναι πάνω από το γράφημα της

άρα το εμβαδόν (που αρχικά ζητείτο) θα είναι ίσο με
![\displaystyle{\begin{aligned}
{\rm E}\left ( \Omega \right ) &=\int_{0}^{1} \left | f(x) -x \right | \, {\rm d}x \\
&=\int_{0}^{1} \left ( x - f(x) \right ) \, {\rm d}x \\
&=\int_{0}^{1} \left [ x - \ln \left ( x + \sqrt{x^2+1} \right ) \right ] \, {\rm d}x \\
&= \sqrt{2} - \frac{1}{2} - \ln \left ( 1+ \sqrt{2} \right ) \approx 0.0328399
\end{aligned}} \displaystyle{\begin{aligned}
{\rm E}\left ( \Omega \right ) &=\int_{0}^{1} \left | f(x) -x \right | \, {\rm d}x \\
&=\int_{0}^{1} \left ( x - f(x) \right ) \, {\rm d}x \\
&=\int_{0}^{1} \left [ x - \ln \left ( x + \sqrt{x^2+1} \right ) \right ] \, {\rm d}x \\
&= \sqrt{2} - \frac{1}{2} - \ln \left ( 1+ \sqrt{2} \right ) \approx 0.0328399
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/9dc377dd628a6bb2462fe77cb461ed34.png)

 για την οποία ισχύουν:
για την οποία ισχύουν:
 έχει μοναδικό σημείο καμπής και προσδιορίστε τα διαστήματα στα οποία η
έχει μοναδικό σημείο καμπής και προσδιορίστε τα διαστήματα στα οποία η  είναι κυρτή ή κοίλη.
είναι κυρτή ή κοίλη. .
. , την διχοτόμο του πρώτου τεταρτημόριου και τις ευθείες
, την διχοτόμο του πρώτου τεταρτημόριου και τις ευθείες  .
.


 . Τώρα
. Τώρα

 είναι
είναι 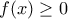 ενώ για
ενώ για  είναι
είναι  . Κατά συνέπεια η
. Κατά συνέπεια η ![(-\infty, 0] (-\infty, 0]](/forum/ext/geomar/texintegr/latexrender/pictures/8bb8e3006289394bd593c5b7a4904dd6.png) και κοίλη στο
και κοίλη στο  .
.
 είναι αρνητική για κάθε
είναι αρνητική για κάθε  .
.![[0, 1] [0, 1]](/forum/ext/geomar/texintegr/latexrender/pictures/264884439b70ab09a86bc848421c6de6.png) η συνάρτησή μας είναι μεγάλυτερη ή ίση του
η συνάρτησή μας είναι μεγάλυτερη ή ίση του  και των ευθειών
και των ευθειών  και
και  είναι ίσο με
είναι ίσο με![\displaystyle{\begin{aligned}
{\rm E}\left ( \Omega \right ) &= \int_{0}^{1} \ln \left ( x + \sqrt{x^2+1} \right ) \, {\rm d}x \\
&= \left [ x \ln \left ( x + \sqrt{x^2+1} \right ) \right ]_0^1 - \int_{0}^{1} \frac{x}{\sqrt{x^2+1}} \, {\rm d}x \\
&= \ln \left ( 1+\sqrt{2} \right ) - \left [ \sqrt{x^2+1} \right ]_0^1 \\
&= \ln \left ( 1+\sqrt{2} \right ) - \sqrt{2} +1 \\
&= 1 - \sqrt{2} + \ln \left ( 1+\sqrt{2} \right ) \approx 0.46716
\end{aligned}} \displaystyle{\begin{aligned}
{\rm E}\left ( \Omega \right ) &= \int_{0}^{1} \ln \left ( x + \sqrt{x^2+1} \right ) \, {\rm d}x \\
&= \left [ x \ln \left ( x + \sqrt{x^2+1} \right ) \right ]_0^1 - \int_{0}^{1} \frac{x}{\sqrt{x^2+1}} \, {\rm d}x \\
&= \ln \left ( 1+\sqrt{2} \right ) - \left [ \sqrt{x^2+1} \right ]_0^1 \\
&= \ln \left ( 1+\sqrt{2} \right ) - \sqrt{2} +1 \\
&= 1 - \sqrt{2} + \ln \left ( 1+\sqrt{2} \right ) \approx 0.46716
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/bcba5ec8faea3465262d8619db96cee6.png)
 είναι η ευθεία
είναι η ευθεία  . Κατά συνέπεια η εφαπτομένη θα είναι πάνω από το γράφημα της
. Κατά συνέπεια η εφαπτομένη θα είναι πάνω από το γράφημα της ![\displaystyle{\begin{aligned}
{\rm E}\left ( \Omega \right ) &=\int_{0}^{1} \left | f(x) -x \right | \, {\rm d}x \\
&=\int_{0}^{1} \left ( x - f(x) \right ) \, {\rm d}x \\
&=\int_{0}^{1} \left [ x - \ln \left ( x + \sqrt{x^2+1} \right ) \right ] \, {\rm d}x \\
&= \sqrt{2} - \frac{1}{2} - \ln \left ( 1+ \sqrt{2} \right ) \approx 0.0328399
\end{aligned}} \displaystyle{\begin{aligned}
{\rm E}\left ( \Omega \right ) &=\int_{0}^{1} \left | f(x) -x \right | \, {\rm d}x \\
&=\int_{0}^{1} \left ( x - f(x) \right ) \, {\rm d}x \\
&=\int_{0}^{1} \left [ x - \ln \left ( x + \sqrt{x^2+1} \right ) \right ] \, {\rm d}x \\
&= \sqrt{2} - \frac{1}{2} - \ln \left ( 1+ \sqrt{2} \right ) \approx 0.0328399
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/9dc377dd628a6bb2462fe77cb461ed34.png)

