 με :
με : 
α) Να δείξετε ότι είναι συνεχής στο

β) Να μελετήσετε την
 ως προς τη μονοτονία και τα ακρότατα
ως προς τη μονοτονία και τα ακρόταταγ) Να υπολογίσετε το εμβαδόν που περικλείεται από τη
 , τον
, τον  και τις ευθείες
και τις ευθείες  και
και 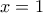
Η ιδέα είναι από T. Andreescu
Συντονιστής: Καρδαμίτσης Σπύρος
 με :
με : 

 ως προς τη μονοτονία και τα ακρότατα
ως προς τη μονοτονία και τα ακρότατα , τον
, τον  και τις ευθείες
και τις ευθείες  και
και 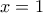
Γεια σου Γιώργη,exdx έγραψε:Δίνεται η συνάρτησημε :
α) Να δείξετε ότι είναι συνεχής στο
β) Να μελετήσετε τηνως προς τη μονοτονία και τα ακρότατα
γ) Να υπολογίσετε το εμβαδόν που περικλείεται από τη, τον
και τις ευθείες
και
Η ιδέα είναι από T. Andreescu
![\displaystyle{\begin{aligned}
\lim_{x\rightarrow 0} x\left [ 2 - \sin \left ( \ln x \right ) -\cos (\ln x) \right ] &=\lim_{x\rightarrow 0} \left ( 2x - x \sin (\ln x) - x \cos (\ln x) \right ) \\
&\overset{(*)}{=}0 - \lim_{x\rightarrow 0} x \sin (\ln x) - \lim_{x\rightarrow 0} x \cos (\ln x) \\
&= 0 - 0 - 0\\
&= 0
\end{aligned}} \displaystyle{\begin{aligned}
\lim_{x\rightarrow 0} x\left [ 2 - \sin \left ( \ln x \right ) -\cos (\ln x) \right ] &=\lim_{x\rightarrow 0} \left ( 2x - x \sin (\ln x) - x \cos (\ln x) \right ) \\
&\overset{(*)}{=}0 - \lim_{x\rightarrow 0} x \sin (\ln x) - \lim_{x\rightarrow 0} x \cos (\ln x) \\
&= 0 - 0 - 0\\
&= 0
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/e3ec0aec2e7be6654c55533e4266a43f.png)
 διότι τα όρια υπάρχουν. Υπολογίζονται με DeL' Hospital. Τα παραλείπω λόγω της επίπονης γραφή τους.
διότι τα όρια υπάρχουν. Υπολογίζονται με DeL' Hospital. Τα παραλείπω λόγω της επίπονης γραφή τους. είναι όντως συνεχής στο
είναι όντως συνεχής στο  .
. είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  ως πράξεις παραγωγίσιμων. Η παράγωγός της δίδεται του τύπου
ως πράξεις παραγωγίσιμων. Η παράγωγός της δίδεται του τύπου με την ισότητα να ισχύει όταν
με την ισότητα να ισχύει όταν  . Άρα η συνάρτησή μας είναι γνήσια αύξουσα. Συνεπώς παρουσιάζει ολικό ελάχιστο στο
. Άρα η συνάρτησή μας είναι γνήσια αύξουσα. Συνεπώς παρουσιάζει ολικό ελάχιστο στο  ίσο με
ίσο με  .
. διότι επειδή η
διότι επειδή η  είναι γνήσια αύξουσα θα ισχύει
είναι γνήσια αύξουσα θα ισχύει  . Τότε:
. Τότε: διότι
διότι![\displaystyle{\begin{aligned}
\int_{0}^{1} x \sin (\ln x) \, {\rm d}x &=\underbrace{\lim_{x\rightarrow 0^+} \int_{x}^{1} t \sin (\ln t) \, {\rm d}t}_{\mathcal{J}} \\
&= \lim_{x\rightarrow 0^+} \left [ \frac{t^2}{2} \sin (\ln t) \right ]_x^1 - \lim_{x\rightarrow 0^+} \int_{x}^{1} \frac{t}{2} \cos (\ln t) \, {\rm d}t \\
&= \cancelto{0}{-\lim_{x\rightarrow 0^+} \frac{x^2}{2} \sin (\ln x)} - \frac{1}{4}\lim_{x\rightarrow 0^+} \left [ t^2 \cos (\ln t) \right ]_x^1 -\frac{1}{4} \lim_{x\rightarrow 0^+} \int_{x}^{1} t \sin (\ln t) \, {\rm d}t \\
&=-\frac{1}{4} - \frac{1}{4} \underbrace{\lim_{x\rightarrow 0^+} \int_{x}^{1} t \sin (\ln t) \, {\rm d}t}_{\mathcal{J}}
\end{aligned}} \displaystyle{\begin{aligned}
\int_{0}^{1} x \sin (\ln x) \, {\rm d}x &=\underbrace{\lim_{x\rightarrow 0^+} \int_{x}^{1} t \sin (\ln t) \, {\rm d}t}_{\mathcal{J}} \\
&= \lim_{x\rightarrow 0^+} \left [ \frac{t^2}{2} \sin (\ln t) \right ]_x^1 - \lim_{x\rightarrow 0^+} \int_{x}^{1} \frac{t}{2} \cos (\ln t) \, {\rm d}t \\
&= \cancelto{0}{-\lim_{x\rightarrow 0^+} \frac{x^2}{2} \sin (\ln x)} - \frac{1}{4}\lim_{x\rightarrow 0^+} \left [ t^2 \cos (\ln t) \right ]_x^1 -\frac{1}{4} \lim_{x\rightarrow 0^+} \int_{x}^{1} t \sin (\ln t) \, {\rm d}t \\
&=-\frac{1}{4} - \frac{1}{4} \underbrace{\lim_{x\rightarrow 0^+} \int_{x}^{1} t \sin (\ln t) \, {\rm d}t}_{\mathcal{J}}
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/0138bef25934da90664fc64b1efbdff5.png) Άρα
Άρα  Όμοια υπολογίζεται και το άλλο. Τελικά:
Όμοια υπολογίζεται και το άλλο. Τελικά:  .
.
Για το α) δεν βλέπω κανένα DeL' Hospital .Απλά είναιTolaso J Kos έγραψε:Γεια σου Γιώργη,exdx έγραψε:Δίνεται η συνάρτησημε :
α) Να δείξετε ότι είναι συνεχής στο
β) Να μελετήσετε τηνως προς τη μονοτονία και τα ακρότατα
γ) Να υπολογίσετε το εμβαδόν που περικλείεται από τη, τον
και τις ευθείες
και
Η ιδέα είναι από T. Andreescu
(α) Πολλά DeL' Hospital βλέπω. Ξεκινάμε:
![\displaystyle{\begin{aligned}
\lim_{x\rightarrow 0} x\left [ 2 - \sin \left ( \ln x \right ) -\cos (\ln x) \right ] &=\lim_{x\rightarrow 0} \left ( 2x - x \sin (\ln x) - x \cos (\ln x) \right ) \\
&\overset{(*)}{=}0 - \lim_{x\rightarrow 0} x \sin (\ln x) - \lim_{x\rightarrow 0} x \cos (\ln x) \\
&= 0 - 0 - 0\\
&= 0
\end{aligned}} \displaystyle{\begin{aligned}
\lim_{x\rightarrow 0} x\left [ 2 - \sin \left ( \ln x \right ) -\cos (\ln x) \right ] &=\lim_{x\rightarrow 0} \left ( 2x - x \sin (\ln x) - x \cos (\ln x) \right ) \\
&\overset{(*)}{=}0 - \lim_{x\rightarrow 0} x \sin (\ln x) - \lim_{x\rightarrow 0} x \cos (\ln x) \\
&= 0 - 0 - 0\\
&= 0
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/e3ec0aec2e7be6654c55533e4266a43f.png)
διότι τα όρια υπάρχουν. Υπολογίζονται με DeL' Hospital. Τα παραλείπω λόγω της επίπονης γραφή τους.
Άρα ηείναι όντως συνεχής στο
.
(β) Ηείναι παραγωγίσιμη στο
ως πράξεις παραγωγίσιμων. Η παράγωγός της δίδεται του τύπου
με την ισότητα να ισχύει όταν
. Άρα η συνάρτησή μας είναι γνήσια αύξουσα. Συνεπώς παρουσιάζει ολικό ελάχιστο στο
ίσο με
.
Ενδιαφέρον εδώ έχει και η κοιλότητα η οποία δε παρουσιάζει κάποια δυσκολία.


 ξεφεύγει από την σχολική ύλη.
ξεφεύγει από την σχολική ύλη.Σταύρο,ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: Στο γ) δεν βλέπω πως μπορούμε να αποφύγουμε τα γενικευμένα.Δηλαδή ξεφεύγει από την σχολική ύλη.
Νομίζω ότι πρέπει να αλλάξει φάκελο.
 χρόνο παρατηρώ ότι είναι πολύ της μόδας ολοκληρώματα αυτού του τύπου. Κυκλοφορούν πολύ στη πιάτσα και σε ορισμένα βοηθήματα, βλέπε π.χ Μπάρλας. Δε ξέρω αν στη νέα έκδοση το 'χει , πάντως στη παλιά που είχα από τότε που ήμουν μαθητής είχε ένα παράδειγμα. Συγκεκριμένα σε λυμένη άσκηση είχε το
χρόνο παρατηρώ ότι είναι πολύ της μόδας ολοκληρώματα αυτού του τύπου. Κυκλοφορούν πολύ στη πιάτσα και σε ορισμένα βοηθήματα, βλέπε π.χ Μπάρλας. Δε ξέρω αν στη νέα έκδοση το 'χει , πάντως στη παλιά που είχα από τότε που ήμουν μαθητής είχε ένα παράδειγμα. Συγκεκριμένα σε λυμένη άσκηση είχε το  .
. είναι συνεχής στο
είναι συνεχής στο  δε νομίζω να υπάρχει κανένα πρόβλημα να ζητηθεί κάτι τέτοιο. Τώρα πώς θα γίνουν οι υπολογισμοί είναι άλλο θέμα. Προσωπική μου άποψη είναι.
δε νομίζω να υπάρχει κανένα πρόβλημα να ζητηθεί κάτι τέτοιο. Τώρα πώς θα γίνουν οι υπολογισμοί είναι άλλο θέμα. Προσωπική μου άποψη είναι.  χρόνια , είχαμε δει αυτήν εδώ (μου έχουν ξεφύγει ορισμένα πράγματα στη λύση είναι γεγονός.) όπου πάλι είχαμε να κάνουμε με γενικευμένο αυτή τη φορά το
χρόνια , είχαμε δει αυτήν εδώ (μου έχουν ξεφύγει ορισμένα πράγματα στη λύση είναι γεγονός.) όπου πάλι είχαμε να κάνουμε με γενικευμένο αυτή τη φορά το  .
.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες